队友:刘雨鑫~
题目:
输入一个二维整形数组,数组里有正数也有负数。
求所有子数组的和的最大值。
思路:
实现思路如下:
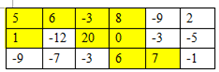
1.先找出二维数组中不包含负数的直接相邻(上下左右相邻)的正整数块。如下图

2.然后转化建模,将该“二维表”与“图”转化,转化方法如下:将每个正整数块看做一个“正元素,将每一个负数看做一个“负元素”,将每一个“正元素”和每一个“负元素”分别作为“图”的结点,其中每个正整数块的和的相反数作为相应“正元素”结点的权值,每个负数的值的相反数作为“负元素”结点的权值,具有直接相邻关系的表中元素,具有双向连通性,结点A与结点B的权值的和定义为从结点A到结点B的“代价”,则该题求最大连通子数组的问题成功转化为求图中的最短路径问题,用弗洛伊德算法可以求出图中每对结点之间的最短路径,遍历求出其中的“代价”最小的一组,再还原出其最短路径,即可找出最大连通子图。
1 package tt20170227; 2 3 import java.util.ArrayList; 4 5 public class lala { 6 7 static int sum; 8 9 public static void main(String[] args) { 10 // TODO Auto-generated method stub 11 12 13 14 System.out.print(la333()); 15 } 16 17 public static int la333() { 18 int[][] a = { { -8, 9, 2, 6 }, { -5, 8, 6, -9 }, { 6, 1, 6, 7 } }; 19 int[][] b = new int[3][4]; 20 // 判断连通性,0为未选中,1为选中,2为连通 21 boolean flag = true; 22 int sum = 0; 23 24 for (int i = 0; i < 3; i++) { 25 for (int j = 0; j < 4; j++) { 26 b[i][j]=0; 27 System.out.print(a[i][j] + " "); 28 if (a[i][j] >= 0) { 29 b[i][j] = 1; 30 } 31 } 32 System.out.println(" "); 33 } 34 35 for (int i = 0; i < 3; i++) { 36 for (int j = 0; j < 4; j++) { 37 if (b[i][j] == 1) { 38 switch(i){ 39 case 0: 40 { 41 switch(j){ 42 case 0: 43 { 44 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) 45 { 46 b[i + 1][j] = 2; 47 } 48 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) 49 { 50 b[i][j + 1] = 2; 51 } 52 break; 53 } 54 case 3: 55 { 56 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) { 57 b[i + 1][j] = 2; 58 } 59 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 60 b[i][j - 1] = 2; 61 } 62 break; 63 } 64 default: 65 { 66 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) { 67 b[i + 1][j] = 2; 68 } 69 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 70 b[i][j - 1] = 2; 71 } 72 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) { 73 b[i][j + 1] = 2; 74 } 75 break; 76 } 77 } 78 break; 79 } 80 case 2: 81 { 82 switch(j){ 83 case 0: 84 { 85 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 86 b[i - 1][j] = 2; 87 } 88 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) { 89 b[i][j + 1] = 2; 90 } 91 break; 92 } 93 case 3: 94 { 95 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 96 b[i - 1][j] = 2; 97 } 98 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 99 b[i][j - 1] = 2; 100 } 101 break; 102 } 103 default: 104 { 105 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 106 b[i - 1][j] = 2; 107 } 108 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 109 b[i][j - 1] = 2; 110 } 111 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) { 112 b[i][j + 1] = 2; 113 } 114 break; 115 } 116 } 117 break; 118 } 119 default: 120 { 121 switch(j){ 122 case 0: 123 { 124 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) { 125 b[i + 1][j] = 2; 126 } 127 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 128 b[i - 1][j] = 2; 129 } 130 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) { 131 b[i][j + 1] = 2; 132 } 133 break; 134 } 135 case 3: 136 { 137 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) { 138 b[i + 1][j] = 2; 139 } 140 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 141 b[i - 1][j] = 2; 142 } 143 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 144 b[i][j - 1] = 2; 145 } 146 break; 147 } 148 default: 149 { 150 if (a[i + 1][j] + a[i][j] > 0 && b[i + 1][j] == 0) { 151 b[i + 1][j] = 2; 152 } 153 if (a[i - 1][j] + a[i][j] > 0 && b[i - 1][j] == 0) { 154 b[i - 1][j] = 2; 155 } 156 if (a[i][j - 1] + a[i][j] > 0 && b[i][j - 1] == 0) { 157 b[i][j - 1] = 2; 158 } 159 if (a[i][j + 1] + a[i][j] > 0 && b[i][j + 1] == 0) { 160 b[i][j + 1] = 2; 161 } 162 break; 163 } 164 } 165 break; 166 } 167 } 168 } 169 System.out.println(a[i][j]); 170 } 171 172 } 173 174 for (int i = 0; i < 3; i++) { 175 for (int j = 0; j < 4; j++) { 176 flag = false; 177 if (b[i][j] != 0 && a[i][j] < 0) { 178 b[i][j] = 0; 179 for (int k = 0; k < 3; k++) { 180 for (int q = 0; q < 4; q++) { 181 if (b[k][q] != 0) { 182 if ((b[k + 1][q] <= 0 || b[k + 1][q] > 2) && (b[k - 1][q] <= 0 || b[k - 1][q] > 2) 183 && (b[k][q + 1] <= 0 || b[k][q + 1] > 2) 184 && (b[k][q - 1] <= 0 || b[k][q - 1] > 2)) { 185 flag = true; 186 } 187 } 188 } 189 190 } 191 if (flag) { 192 b[i][j] = 2; 193 } 194 } 195 } 196 } 197 198 for (int i = 0; i < 3; i++) { 199 for (int j = 0; j < 4; j++) { 200 if (b[i][j] != 0) { 201 System.out.print(a[i][j] + " "); 202 sum += a[i][j]; 203 } 204 } 205 System.out.println(" "); 206 207 } 208 209 return sum; 210 } 211 }
总结:思路有,可是还是没有具体实现,在课下会多思考,争取实现。