【异常检测】孤立森林（Isolation Forest）算法简介

简介

工作的过程中经常会遇到这样一个问题，在构建模型训练数据时，我们很难保证训练数据的纯净度，数据中往往会参杂很多被错误标记噪声数据，而数据的质量决定了最终模型性能的好坏。如果进行人工二次标记，成本会很高，我们希望能使用一种无监督算法帮我们做这件事，异常检测算法可以在一定程度上解决这个问题。

异常检测分为 离群点检测(outlier detection) 以及 奇异值检测(novelty detection) 两种.

• 离群点检测：适用于训练数据中包含异常值的情况，例如上述所提及的情况。离群点检测模型会尝试拟合训练数据最集中的区域，而忽略异常数据。
• 奇异值检测：适用于训练数据不受异常值的污染，目标是去检测新样本是否是异常值。 在这种情况下，异常值也被称为奇异点。

孤立森林 (Isolation Forest, iForest)是一个基于Ensemble的快速离群点检测方法，具有线性时间复杂度和高精准度，是符合大数据处理要求的State-of-the-art算法。由南京大学周志华教授等人于2008年首次提出，之后又于2012年提出了改进版本。适用于连续数据(Continuous numerical data)的异常检测，与其他异常检测算法通过距离、密度等量化指标来刻画样本间的疏离程度不同，孤立森林算法通过对样本点的孤立来检测异常值。具体来说，该算法利用一种名为孤立树iTree的二叉搜索树结构来孤立样本。由于异常值的数量较少且与大部分样本的疏离性，因此，异常值会被更早的孤立出来，也即异常值会距离iTree的根节点更近，而正常值则会距离根节点有更远的距离。此外，相较于LOF，K-means等传统算法，孤立森林算法对高纬数据有较好的鲁棒性。其可以用于网络安全中的攻击检测，金融交易欺诈检测，疾病侦测，和噪声数据过滤等。

举个例子：

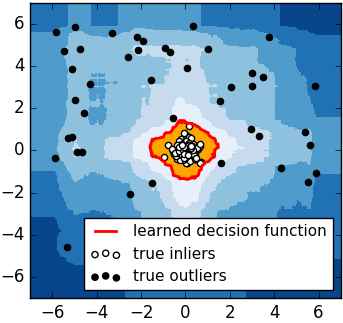
对于如何查找哪些点是否容易被孤立，iForest使用了一套非常高效的策略。假设我们用一个随机超平面来切割数据空间, 切一次可以生成两个子空间（想象拿刀切蛋糕一分为二）。之后我们再继续用一个随机超平面来切割每个子空间，循环下去，直到每子空间里面只有一个数据点为止。直观上来讲，我们可以发现那些密度很高的簇是可以被切很多次才会停止切割，但是那些密度很低的点很容易很早的就停到一个子空间了。上图里面黑色的点就很容易被切几次就停到一个子空间，而白色点聚集的地方可以切很多次才停止。

算法

怎么来切这个数据空间是iForest的设计核心思想，本文仅介绍最基本的方法。由于切割是随机的，所以需要用Ensemble的方法来得到一个收敛值（蒙特卡洛方法），即反复从头开始切，然后平均每次切的结果。iForest 由 T 个 iTree 组成，每个 iTree 是一个二叉树结构。该算法大致可以分为两个阶段，第一个阶段我们需要训练出 T 颗孤立树，组成孤立森林。随后我们将每个样本点带入森林中的每棵孤立树，计算平均高度，之后再计算每个样本点的异常值分数。

第一阶段，步骤如下：

1. 从训练数据中随机选择Ψ个点样本点作为样本子集，放入树的根节点。
2. 随机指定一个维度（特征），在当前节点数据中随机产生一个切割点 p（切割点产生于当前节点数据中指定维度的最大值和最小值之间）。
3. 以此切割点生成了一个超平面，然后将当前节点数据空间划分为2个子空间：把指定维度里小于 p 的数据放在当前节点的左子节点，把大于等于 p 的数据放在当前节点的右子节点。
4. 在子节点中递归步骤(2)和(3)，不断构造新的子节点，直到子节点中只有一个数据（无法再继续切割）或子节点已到达限定高度。
5. 循环(1)至(4)，直至生成 T 个孤立树iTree。

第二阶段：

获得T个iTree之后，iForest训练就结束，然后我们可以用生成的iForest来评估测试数据了。对于每一个数据点 (x_i)，令其遍历每一颗孤立树iTree，计算点 (x_i) 在森林中的平均高度 (h(x_i)) ，对所有点的平均高度做归一化处理。异常值分数的计算公式如下所示：

[Sleft ( x,psi ight )= 2^{-frac{Eleft ( hleft ( x ight ) ight )}{cleft ( psi ight )}} ]

其中

[cleft ( psi ight ) = left{egin{matrix} 2Hleft ( psi - 1 ight ) - 2 left ( psi - 1 ight )/psi, psi > 2\ 1, quad quad quad quad quad quad quad quad quad quad psi = 2\ 0, quad quad quad quad quad quad quad quad otherwise end{matrix} ight. ]

(H(i)) 是调和数，可以通过 ln(i) + 0.5772156649（欧拉常数）来估算。分值越小表示数据越为异常。

示例：

>>> from sklearn.ensemble import IsolationForest
>>> X = [[-1.1], [0.3], [0.5], [100]]
>>> clf = IsolationForest(random_state=0).fit(X)
>>> clf.predict([[0.1], [0], [90]])
array([ 1,  1, -1])

补充：

1. iForest具有线性时间复杂度。因为是Ensemble的方法，所以可以用在含有海量数据的数据集上面。通常树的数量越多，算法越稳定。由于每棵树都是互相独立生成的，因此可以部署在大规模分布式系统上来加速运算。

2. iForest不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度，建完树后仍然有大量的维度信息没有被使用，导致算法可靠性降低。高维空间还可能存在大量噪音维度或无关维度(irrelevant attributes)，影响树的构建。对这类数据，建议使用子空间异常检测(Subspace Anomaly Detection)技术。此外，切割平面默认是axis-parallel的，也可以随机生成各种角度的切割平面，详见“On Detecting Clustered Anomalies Using SCiForest”。

3. iForest仅对Global Anomaly敏感，即全局稀疏点敏感，不擅长处理局部的相对稀疏点(Local Anomaly)。目前已有改进方法发表于PAKDD，详见“Improving iForest with Relative Mass”。

4. iForest推动了重心估计(Mass Estimation)理论发展，目前在分类聚类和异常检测中都取得显著效果，发表于各大顶级数据挖掘会议和期刊(如SIGKDD，ICDM，ECML)。

参考文章：

孤立森林（Isolation Forest）算法简介

iForest （Isolation Forest）孤立森林 异常检测 入门篇

Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. "Isolation forest."Data Mining, 2008. ICDM'08. Eighth IEEE International Conference on. IEEE, 2008.

Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. "Isolation-based anomaly detection."ACM Transactions on Knowledge Discovery from Data (TKDD)6.1 (2012): 3.