- 概述
- 初中阶段的电路几乎都是分析电阻,故整理常用的电阻分析方法如下
- 目录
有些名字是我瞎编的- 简单电路
- 基本等价变换
- 对称电路
- 简单电路
- 基本关系
设第$i$个电阻大小为$R_i$- 串联
- 根据性质“电流相同”,得电阻为$Sigma^{n}_{i=1}{R_i}$
- 并联
- 根据性质“电压相同”,得电阻为$frac{1}{Sigma^{n}_{i=1}{frac{1}{R_i}}}$
- 串联
- 转换方法
- 将局部成简单关系的电阻合并,不断重复此过程,可以证明剩下的网络永远是简单电路
- 基本关系
- 等位点
- 到两端点的电路全等的点的电压相等
- 如果两个点关于要求的两个端点对称,那么它们的电压相等
- 如果两个点电压相等,可以将这两个点短路或断路
- 基本等价变换
- 性质
- 无电阻的导线可以在保持联通情况下随意变换
- 应用
- 改变线的形状
- 将弯曲的线变成折线,符合电路图标准
- 将立体的图摊平,便于分析
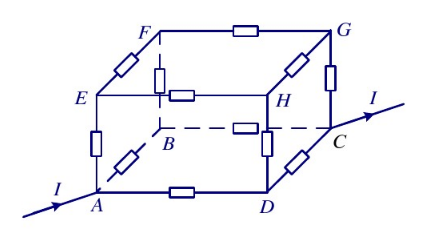 可以变为
可以变为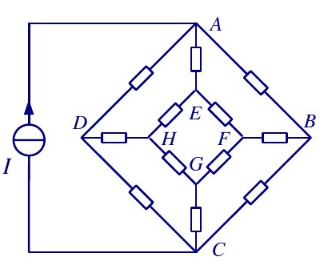
- 缩点,拆点
 可以变为
可以变为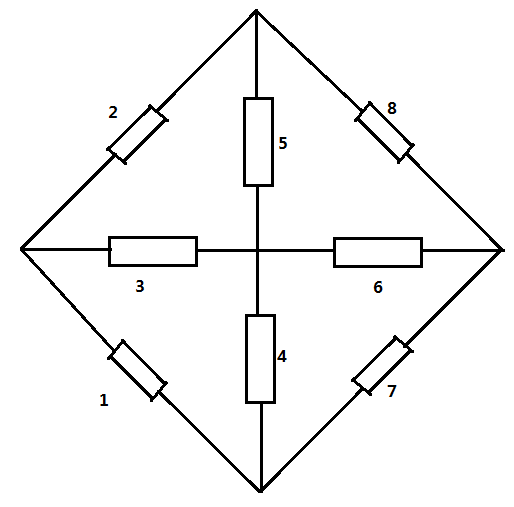
-
移动装置
-
电流表、电阻表等可以自由地在无电阻的导线上运动
- 电阻可以在不改变串并联关系的情况下自由移动
-
- 改变线的形状
- 性质
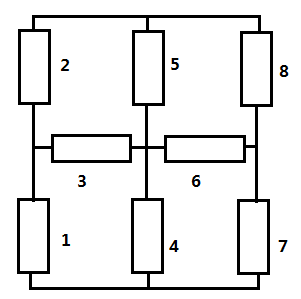
- 对称电路
内容较为复杂,具体见我的blog对称电路- 轴对称电路
- 对于轴对称电路,我们将不交叉的部分变成开路,交叉部分短路

- 对于轴对称电路,我们将不交叉的部分变成开路,交叉部分短路
- 中心对称电路
- (和轴对称的性质相反)将原网络的平行线断开后连上下颠倒的线,将交线断开后保持开路
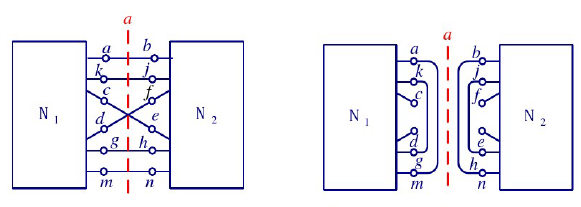
- (和轴对称的性质相反)将原网络的平行线断开后连上下颠倒的线,将交线断开后保持开路
- 轴对称电路
- 实际问题
- 有电阻的导线
- 在导线中央加入一个电阻
- 电阻片
- 将电阻片分解成几个可计算部分,转化为电路
- 例子
- 求$R_{AB}$与$R_{CD}$电阻之比

- 分割后发现每一个部分都是全等的,所以可以将电阻转化为电路图
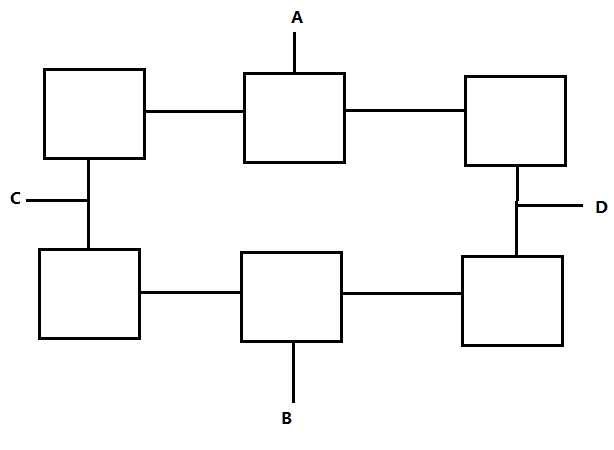
- 分割后发现每一个部分都是全等的,所以可以将电阻转化为电路图
-
求等效电路图
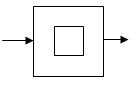
-
将图转化为
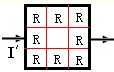
-
等效电路为

-
- 求$R_{AB}$与$R_{CD}$电阻之比
- 有电阻的导线