本文旨在了解一下几点:
- 对极约束是什么
- 基础矩阵F
- F的秩有什么意义
- 本质矩阵E
- E与F的区别与联系
对极约束
目的
在已知 2D像素坐标的前提下,根据两幅图像间多组2D像素点对来估计相机的运动。
概念
推导过程
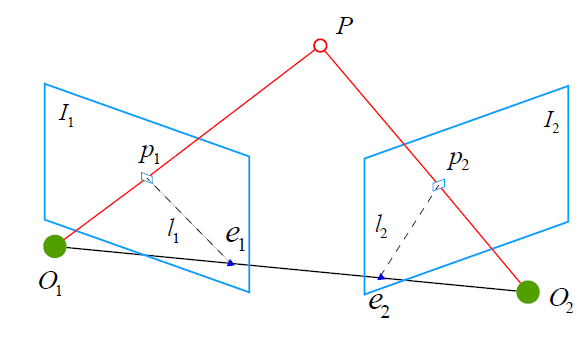
如上图所示,我们希望求取两帧图像 $I_1$,$ I_2$ 之间的运动,设第一帧到第二帧的运动为 $R$,$t$。两个相机中心分别为 $O_1$,$O_2$。现在,考虑 $I_1$ 中有一个特征点 $p_1$,它在 $I_2$ 中对应着特征点 $p_2$。我们知道两者是通过特征匹配得到的。首先,连线 $O_2P$与$O_1P$ 在三维空间中会相交于点 P。由$O_1$, $O_2$, $P$ 三点确定的平面为极平面(Epipolar plane)。$O_1O_2$ 连线与像平面 $I_1$, $I_2$ 的交点$e_1$, $e_2$ 称为极点(Epipoles),$O_1O_2$ 被称为基线(Baseline)。我们称极平面与两个像平面 $I_1$, $I_2$ 之间的相交线 $l_1$, $l_2$ 为极线(Epipolar line)。
设P的空间位置为 $P=[X,Y,Z]^T$。则根据针孔模型,两个像素点$p_1,p_2$的像素位置为:
$$
s_1p_1=KP,s_2p_2=K(RP+t)
$$
其中,K为相机内参矩阵,R,t为两个坐标系的相机运动。具体来说,计算的是$R_{21}$,$t_{21}$,因为他们把第一个坐标系下的坐标转换到了第二个坐标系下。其也可写作是李代数形式。
尺度意义下相等记作:$spsimeq p$,可表示投影关系。
因此有:
$$
x_1=K^{-1}p_1, x_2=K^{-1}p_2
$$
其中,$x_1$,$x_2$表示像素点在归一化平面上的坐标。代入上式,得:
$$
x_2simeq Rx_1+t
$$
两边同时左乘t^。因此得到:
$$
t^{.}x_2simeq t^{.}Rx_1
$$
然后同时左乘x2^,得到
重新带入$p_1,p_2$有:
上述两式称为对极约束。
几何意义: $O_1,P,O_2$三者共面。
把中间部分记作两个矩阵,基础矩阵F和本质矩阵E,可进一步检核对极约束:E=t^R,$F=K^{-T}EK^{-1}$,$x^T_2Ex^1=p^T_2Fp_1=0$。
可看出,对极约束简洁地给出了两个匹配点之间的中间位置关系。
于是位子估计变为以下两部:
- 根据配对点的像素为最初求出E或者F。
- 根据E或者F求出R,t。
由于E和F只相差了相机内参,而内参在SLAM通常是已知的,因此实践中往往使用形式更简单的E。