1、时间复杂度分析有哪些?
- 最好情况时间复杂度(best case time complexity)
- 最坏情况时间复杂度(worst case time complexity)
- 平均情况时间复杂度(average case time complexity)
- 均摊时间复杂度(amortized time complexity)
2、最好、最坏情况时间复杂度。
最好情况时间复杂度就是在最理想的情况下,执行这段代码的时间复杂度。
最坏情况时间复杂度就是在最糟糕的情况下,执行这段代码的时间复杂度。
// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
上面这段代码要实现的功能是:在一个数组中查找变量 x 出现的位置,如果找到了,就马上跳出循环,返回它的位置值;如果找不到,就返回 -1。
这里不能只是看到了 for 循环就判定其时间复杂度为 O(n),因为这个数组的顺序是不确定的,有可能数组中的第一个元素就是 x,那就可以马上结束循环了,其时间复杂度就是 O(1);如果数组中不存在变量 x 或者是数组中的最后一个元素才是 x,那就需要遍历整个数组,时间复杂度就是 O(n)。
在这里,O(1) 就是最好情况时间复杂度,O(n) 就是最坏情况时间复杂度。
3、平均情况时间复杂度
最好、最坏情况时间复杂度都是极端情况下的代码复杂度,发生的概率很小。因此,我们还需要知道平均情况时间复杂度。
还是以刚刚查找变量 x 的位置的例子为例,要查找的变量 x 在数组中的位置,总共有 n+1 种情况:在数组的 0~n-1 位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来再除以 n+1,就可以得到需要遍历的元素个数的平均值,即:

省略掉系数、低阶、常量,将以上公式进行简化之后,得到的平均时间复杂度就是 O(n)。
但是,以上的 n+1 种情况,没有将各种情况发生的概率考虑进去。这里可以引入概率论的相关知识,假设变量 x 在数组中与不在数组中的概率各为 1/2,出现在 0~n-1 这 n 个位置的概率都是 1/n。根据概率乘法法则,要查找的数据出现正在 0~n-1 中任意位置的概率就是 1/(2n)。
这样,就可以得到以下计算过程:
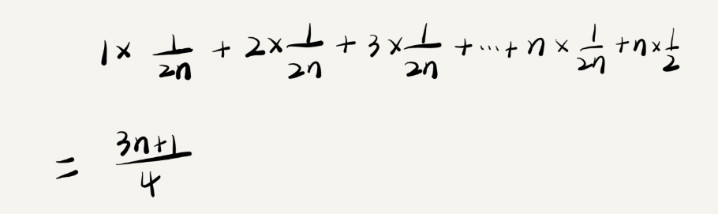
这个值就是概率论中的加权平均值,也叫做期望值。根据这个加权平均值,去掉系数和常量,我们得到的平均时间复杂度也是 O(n)。所以,平均时间复杂度就是:加权平均时间复杂度(亦称为期望时间复杂度)。
大部分情况下,我们并不需要区分最好、最坏、平均三种复杂度,平均复杂度只在某些特殊情况下才用到。
4、均摊时间复杂度
均摊时间复杂度:对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度较高。而且这些操作之间存在前后连贯的时序关系,在这个时候,我们可以将这一组操作放在一块儿分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度较低的操作上。
均摊时间复杂度的应用场景比平均时间复杂度更加特殊、更加有限。
// array表示一个长度为n的数组
// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;
void insert(int val) {
if (count == array.length) {
int sum = 0;
for (int i = 0; i < array.length; ++i) {
sum = sum + array[i];
}
array[0] = sum;
count = 1;
}
array[count] = val;
++count;
}
这段代码实现的是往一个数组中插入数据的功能,当数组满了以后,也就是 count == array.length 的时候,我们用 for 循环遍历数组求和,再将新的数据插入,其时间复杂度为 O(n)。但如果数组未满,则直接将数据插入数组,其时间复杂度为 O(1)。
个人体会: 平均和均摊基本算是一个概念,均摊是特殊的平均。出现O(1)的次数远大于出现O(n)出现的次数,那么平均和均摊时间复杂度就是O(1)。
我们来分析一下它的时间复杂度,数组的长度为 n,根据数据插入的不同位置,可以分为 n 种情况,每种情况的时间复杂度为 O(1)。还有一种最“糟糕”的情况,那就是数组已满,这个时候的时间复杂度为 O(n)。而且,这 n+1 种情况发生的概率是一样的,都是 1/(n+1)。所以,根据加权平均的计算方法,可知:
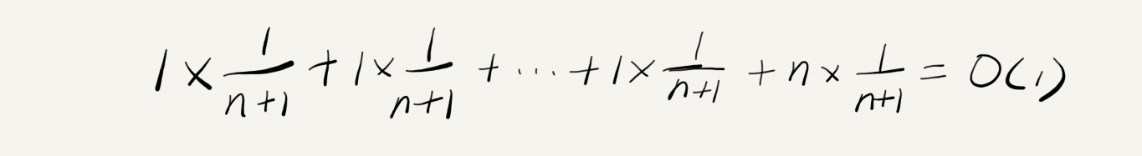
对比一下 insert() 的例子和前面 find() 的例子,这两个例子的最好、最坏情况时间复杂度都一样,为什么平均时间复杂度相差这么多呢?
这两个例子之间最大的区别在于:find() 的最好、最坏情况时间复杂度都是在极端情况下才会发生,而 insert() 在大部分情况下,时间复杂度都是 O(1),只有在极端情况下,时间复杂度才是 O(n)。其次,对于 insert() 函数来说,每当碰到一个时间复杂度为 O(n) 的情况,接下来就会有 n-1 个 O(1) 的插入操作,循环往复。
均摊下来,这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊时间复杂度分析的大致思路。