题目描述


有源汇上下界最小费用最大流
同上下界网络流,把u->v拆成S'->v、u->v和u->T'三条边,其中S'->v和u->v有代价
也可以求出每个点的出入情况D[i],表示(流入-流出)
如果D[i]>0则连S'->i,否则连i->T'
本质是强制必经边满流,然后再平衡流量
然后跑S'->T'求出可行流,再跑原S->T求出最大流
费用流消负环
可以用消圈算法,但是很慢,考虑用上面的"退流"思想
新建源汇点S''和T'',若一条边的代价<0则强制将其满流,计入答案的同时求出每个点的出入情况E[i]
如果E[i]>0则连S''->i,否则连i->T''
然后跑S''->T''的最小费用最大流即可消掉负环
一点思(kou)考(hu)
当一个费用流图无负环时,增广一次后为什么不会出现负环?
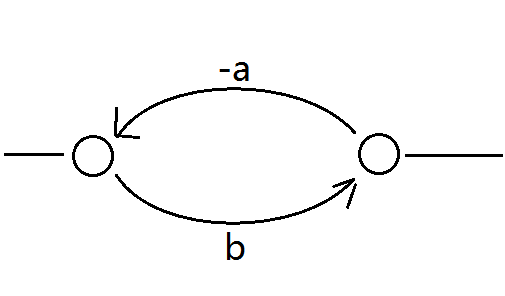
这是跑完之后的图,假设中间的是负环
若出现负环(跑完之后出现),则说明增广路径上存在uv两点,使得路径上u->v的距离a和不经过增广路径的距离b满足b-a<0
也就是b<a,那么必然会跑更短的路径,所以矛盾
更复杂的情况同理
code
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define max(a,b) (a>b?a:b)
#define min(a,b) (a<b?a:b)
#define ll long long
#define file
using namespace std;
struct tree{
int a[701][2],ls[161],s[161],S[161],len,i,j,k,l;
void New(int x,int y) {++len;a[len][0]=y;a[len][1]=ls[x];ls[x]=len;}
void dfs(int Fa,int t)
{
int i;
for (i=ls[t]; i; i=a[i][1])
if (a[i][0]!=Fa)
{
s[a[i][0]]=s[a[i][0]]+s[t];
dfs(t,a[i][0]);
S[t]+=S[a[i][0]];
}
}
} tr;
int a[3001][4],A[161],B[161],A2[161],B2[161],ls[161],fa[161],S[161],T[161],pa[161],pb[161],
f[161],g[161],G[161],d[1000001],D[161],E[161],n,m,i,j,k,l,len,st,ed,ans,h,t,sum,St,Ed;
bool bz[161];
void New(int x,int y,int f,int w)
{
++len;
a[len][0]=y;
a[len][1]=ls[x];
ls[x]=len;
a[len][2]=f;
a[len][3]=w;
}
void NEW(int x,int y,int f,int w)
{
if (!f) return;
if (w<0)
{
ans+=f*w,E[y]+=f,E[x]-=f;
New(x,y,0,w);
New(y,x,f,-w);
return;
}
New(x,y,f,w);
New(y,x,0,-w);
}
void add(int x,int y,int A,int B,int w)
{
if (A>B)
{
printf("-1
");
exit(0);
}
ans+=A*w;
D[y]+=A,D[x]-=A;
NEW(x,y,B-A,w);
}
void work(int st,int ed)
{
int i,j,k,l;
while (1)
{
h=0;t=1;
d[1]=st;
memset(f,127,sizeof(f));
f[st]=0;
bz[st]=1;
while (h<t)
{
for (i=ls[d[++h]]; i; i=a[i][1])
if (a[i][2] && f[d[h]]+a[i][3]<f[a[i][0]])
{
f[a[i][0]]=f[d[h]]+a[i][3];
g[a[i][0]]=d[h];
G[a[i][0]]=i;
if (!bz[a[i][0]] && a[i][0]!=ed)
d[++t]=a[i][0],bz[a[i][0]]=1;
}
bz[d[h]]=0;
}
if (f[ed]>2000000000) break;
sum=2000000000;
for (i=ed; i!=st; i=g[i])
sum=min(sum,a[G[i]][2]);
ans+=sum*f[ed];
for (i=ed; i!=st; i=g[i])
a[G[i]][2]-=sum,a[G[i]^1][2]+=sum;
}
}
int main()
{
freopen("C.in","r",stdin);
#ifdef file
freopen("C.out","w",stdout);
#endif
scanf("%d%d",&n,&m);len=1;st=n+3,ed=n+4;St=n+5,Ed=n+6;
fo(i,2,n) scanf("%d%d%d%d%d",&fa[i],&A[i],&B[i],&A2[i],&B2[i]),tr.New(fa[i],i),tr.s[i]=B2[i];
fo(i,1,m)
{
scanf("%d%d%d%d",&S[i],&T[i],&pa[i],&pb[i]);
++tr.S[T[i]];--tr.S[S[i]];
}
tr.dfs(0,1);
// ---
fo(i,2,n)
add(i,fa[i],max(0,tr.S[i]-B[i]),min(A[i],tr.S[i]),A2[i]);
fo(i,1,m)
ans+=pa[i],add(n+1,T[i],0,1,0),add(S[i],n+2,0,1,0),add(T[i],S[i],0,1,pb[i]-pa[i]+(tr.s[T[i]]-tr.s[S[i]]));
k=len;
add(n+2,n+1,0,2133333333,0);
fo(i,1,Ed) if (D[i]>0) NEW(st,i,D[i],0); else if (D[i]<0) NEW(i,ed,-D[i],0); //上下界
l=len;
fo(i,1,ed) if (E[i]>0) NEW(St,i,E[i],0); else if (E[i]<0) NEW(i,Ed,-E[i],0); //负环
// ---
work(St,Ed); //负环
fo(i,1,ed)
while (ls[i]>l)
ls[i]=a[ls[i]][1];
work(st,ed); //上下界
fo(i,1,n+2)
while (ls[i]>k)
ls[i]=a[ls[i]][1];
work(n+1,n+2); //最大流
// ---
for (i=ls[st]; i; i=a[i][1])
if (a[i][2])
{
printf("-1
");
return 0;
}
printf("%d
",ans);
fclose(stdin);
fclose(stdout);
return 0;
}
参考资料
https://www.cnblogs.com/leason-lyx/p/11144527.html
https://www.cnblogs.com/Miracevin/p/10028021.html
https://www.itdaan.com/blog/2012/11/20/e12975f2853632e9c471b1b375b5cac7.html