6409. 【NOIP2019模拟11.06】困难的图论（Tarjan求点双）

题目描述

Description

给定由 n 个点 m 条边组成的无向连通图，保证没有重边和自环。
你需要找出所有边，满足这些边恰好存在于一个简单环中。一个环被称为简单环，当且仅当它包含的所有点都只在这个环中被经过了一次。
注意到这些边可能有很多条，你只需要输出他们编号的异或和即可。

Input

第一行两个数 n, m。
接下来 m 行，每行两个数 ai , bi，表示第 i 条边连接了 ai , bi。

Output

输出一个数，表示所有满足条件的边的编号的异或和。

Sample Input

Sample Input1
4 4
1 2
2 4
4 3
3 2


Sample Input2
4 5
1 2
1 3
2 4
4 3
3 2 
 

Sample Output

Sample Output2
5

Sample Output2
0



对于第一个样例，2,3,4 满足要求。
对于第二个样例，所有边都不满足要求。 
 

Data Constraint

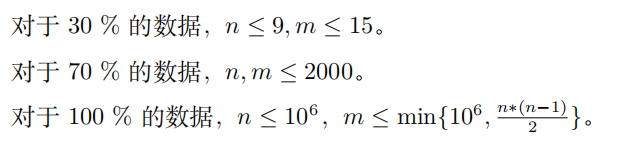
题解

复习求点双

先拓扑去掉树边，剩下的是若干个相连的点双，Tarjan即可

一些注意事项：

1、栈存的是边

2、求边双or点双时的low要做完之后再赋值（或者在返祖边时把dfn赋过去）

3、记录点双中的边：

只需要记录向下的边和向上的返祖边（不能直接指向父亲）即可，弹栈时一直弹到当前的t

如果相邻两点不在同一个点双中，那么显然栈顶的边是父亲-->儿子，可以直接弹

code

有重边所以打表

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;

int a[2000002][2];
int ls[2000002];
int d[2000002];
int D[2000002];
int d2[2000002][2];
int d3[2000002];
bool BZ[2000002];
bool bz[2000002];
bool Bz[2000002];
int dfn[2000002];
int low[2000002];
int n,m,root,i,j,k,l,len,h,t,ans,tot,sum,s1,s2,T;

void New(int x,int y)
{
	++len;
	a[len][0]=y;
	a[len][1]=ls[x];
	ls[x]=len;
}

void dfs2(int Fa,int t)
{
	int i;
	
	Bz[t]=1;
	
	for (i=ls[t]; i; i=a[i][1])
	if (!bz[i] && a[i][0]!=Fa && !Bz[a[i][0]])
	{
		dfs2(t,a[i][0]);
		tot+=t==root;
	}
}

void work()
{
	sum^=d2[l][1]/2;
	++s1;
	if (!BZ[d2[l][0]])
	{
		++s2;
		BZ[d2[l][0]]=1;
		d3[++T]=d2[l][0];
	}
	--l;
}

void pop(int t)
{
	int i;
	
	sum=0;s1=0;s2=0;T=0;
	while (d2[l][0]!=t)
	work();
	work();
	
	if (s1==s2) ans^=sum;
	fo(i,1,T) BZ[d3[i]]=0;
}

void dfs(int Fa,int t)
{
	int i,Low=++j;
	
	Bz[t]=1;
	dfn[t]=j;
	low[t]=j;
	
	for (i=ls[t]; i; i=a[i][1])
	if (!bz[i] && a[i][0]!=Fa)
	{
		if (!Bz[a[i][0]] || dfn[a[i][0]]<dfn[t])
		{
			++l;
			d2[l][0]=t;
			d2[l][1]=i;
		}
		
		if (!Bz[a[i][0]])
		{
			dfs(t,a[i][0]);
			
			if ((t!=root || tot>1) && dfn[t]<=low[a[i][0]])
			{
				if (d2[l][0]==t)
				{
					--D[d2[l][0]];
					--D[a[d2[l][1]][0]];
					--l;
				}
				else
				pop(t);
			}
		}
		Low=min(Low,low[a[i][0]]);
	}
	
	if (t==root && l)
	{
		if (d2[l][0]==t)
		{
			--D[d2[l][0]];
			--D[a[d2[l][1]][0]];
			--l;
		}
		else
		pop(t);
	}
	low[t]=Low;
}

int main()
{
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	
	scanf("%d%d",&n,&m);
	
	if (n==9 && m==12) //chongbian
	{
		printf("0
");
		return 0;
	}
	
	len=1;
	fo(i,1,m)
	{
		scanf("%d%d",&j,&k);
		
		New(j,k);
		New(k,j);
		
		++D[j];++D[k];
	}
	
	h=0;
	fo(i,1,n)
	if (D[i]==1)
	d[++t]=i;
	
	while (h<t)
	{
		for (i=ls[d[++h]]; i; i=a[i][1])
		if (!bz[i])
		{
			bz[i]=1;
			bz[i^1]=1;
			
			--D[d[h]];
			--D[a[i][0]];
			
			if (D[a[i][0]]==1)
			d[++t]=a[i][0];
		}
	}
	
	fo(i,1,n)
	if (D[i])
	{
		root=i;
		dfs2(0,root);
		
		j=0;
		l=0;
		memset(Bz,0,sizeof(Bz));
		dfs(0,root);
		break;
	}
	
	printf("%d
",ans);
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}