构建乘积数组

题目描述

给定一个数组A[0,1,...,n-1]，请构建一个数组B[0,1,...,n-1]，其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。

（注意：规定B[0] = A[1] * A[2] * ... * A[n-1]，B[n-1] = A[0] * A[1] * ... * A[n-2]）

对于A长度为1的情况，B无意义，故而无法构建，因此该情况不会存在。

示例1：

输入：[1,2,3,4,5]
输出：[120,60,40,30,24]

解题思路

借用一张图

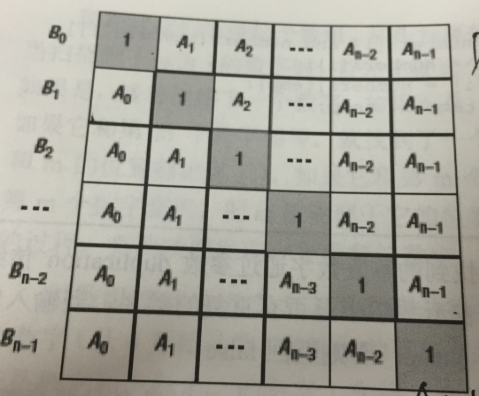
可以看出，每一个B[i]都是除了第i个A[i]之外，所有的A数组元素之积。

思路1：

最笨的思路，即每求一次B，都去遍历一次A数组，然后遇到第i个后，跳过继续执行下一步，直至遍历完A数组，代码如下：

public class Solution {
    public int[] multiply(int[] A) {
        int[] B = new int[A.length];
        if(A==null || A.length<=1){
            return B;
        }
        for(int i = 0; i<A.length; i++){
            B[i] = com(A,i);
        }
        return B;
    }
    public int com(int[] A,int k){
        int res = 1;
        for(int i = 0; i<A.length; i++){
            res = (i==k?res:A[i]*res);
        }
        return res;
    }
}

但是这样显然运算速度是比较慢的，因为你做了一些重复性的计算。

比如，在计算第i个B时，即B[i]，你需要可以先计算出A[0]*...*A[i-2]*A[i-1]，然后再计算A[i+1]*...*A[n-2]*A[n-1]。那么在你计算A[0]*...*A[i-2]*A[i-1]时，其实，在前一步求B[i-1]时，你已经计算过A[0]*...*A[i-2]了，故如果将该值存储起来，那么在这里就可以直接使用。这就是动态规划嘛，是不是？

好，看明白之后，代码如下：

public class Solution {
    public int[] multiply(int[] A) {
        int[] B = new int[A.length];
        int res=1;
　　　　　//求下三角
        B[0]=1;
        for(int i = 1; i<A.length; i++){
           B[i] = B[i-1]*A[i-1];
        }
　　　　 //求上三角
        int[] C = new int[A.length];
        C[A.length-1] = 1;
        for(int j=A.length-2; j>=0; j--){
            C[j] = C[j+1]*A[j+1];
        }
　　　　 //综合起来
        for(int k =0; k<A.length; k++){
            B[k] *= C[k];
        }
        
        return B;
    }
}

这里，其实还可以优化一下就是，可以不使用C这个数组，这样就节省了少许空间，代码如下：

public class Solution {
    public int[] multiply(int[] A) {
        int[] B = new int[A.length];
        int res=1;
        B[0]=1;
        for(int i = 1; i<A.length; i++){
           B[i] = B[i-1]*A[i-1];
        }
       int temp =1;
        for(int j=A.length-2; j>=0; j--){
            temp *= A[j+1];
            B[j] *= temp;
        }
        
        return B;
    }
}

Over......