神题!这个构造考试的时候想了好久www
假设我们现在要对n个点做这个操作,假设把n个点的度数都拉满。然后每次选择n个点以外的某一个点让某些点的度数都-1
那么很容易构想出一种办法,假设一开始每个点的度数都为n,那么我们选择一个点向n个点连边,然后选择这个点,这样下一次选择的最大只能是度数为n-1的点,我们继续这样的操作,假设第i轮最大的度数点为i,那么能在n个点外搞出n/i个点,这样题目中的程序的点个数为nlogn个,而我们只需要删除n个点即可。只要把n取大一点,使nlogn>3n即可。
唔,可以说是考试的时候不敢开,看了题解的题目解释感觉清楚多了。就是给你一个二分图,每次某些点可以选,然后问有多少种选点情况,使得被选的点存在完美匹配。
这状压hall定理裸题啊。答案就是ansleft*ansright-1,复杂度低得很,最劣情况也就是一组数据qn*2^n
找三元环,经典问题,暴力n^3枚举即可,但是实际上在n^2就会找到解了,但是证明比较玄学。
这里给出比较简单的解释
显然,当人数大于等于 6 时其结果一定是 Bad Team! 。(拉姆齐定理,等同于使用两种颜色给 Kn 的边染色,当 n >= 6 时图中一定存在同色三角形)
这题也比较妙。首先查看题目可以发现需求复杂度O(n)算法,考虑kmp或SAM。我们发现如果我们对第二个字符串反串建立KMP,然后在第一个字符串上面跑,那么每次跳fail的时候,比如i->fail[i],因为每个被匹配的字符的贡献是1,说明总贡献增加了i*(i+1)/2。那么直接KMP统计贡献即可
这题就比较有趣了,想法是队友想出来的,显然在%4==0的时候,是个斜正方形,那么我们考虑每次增加一条边应该怎么增加答案,如下图所示
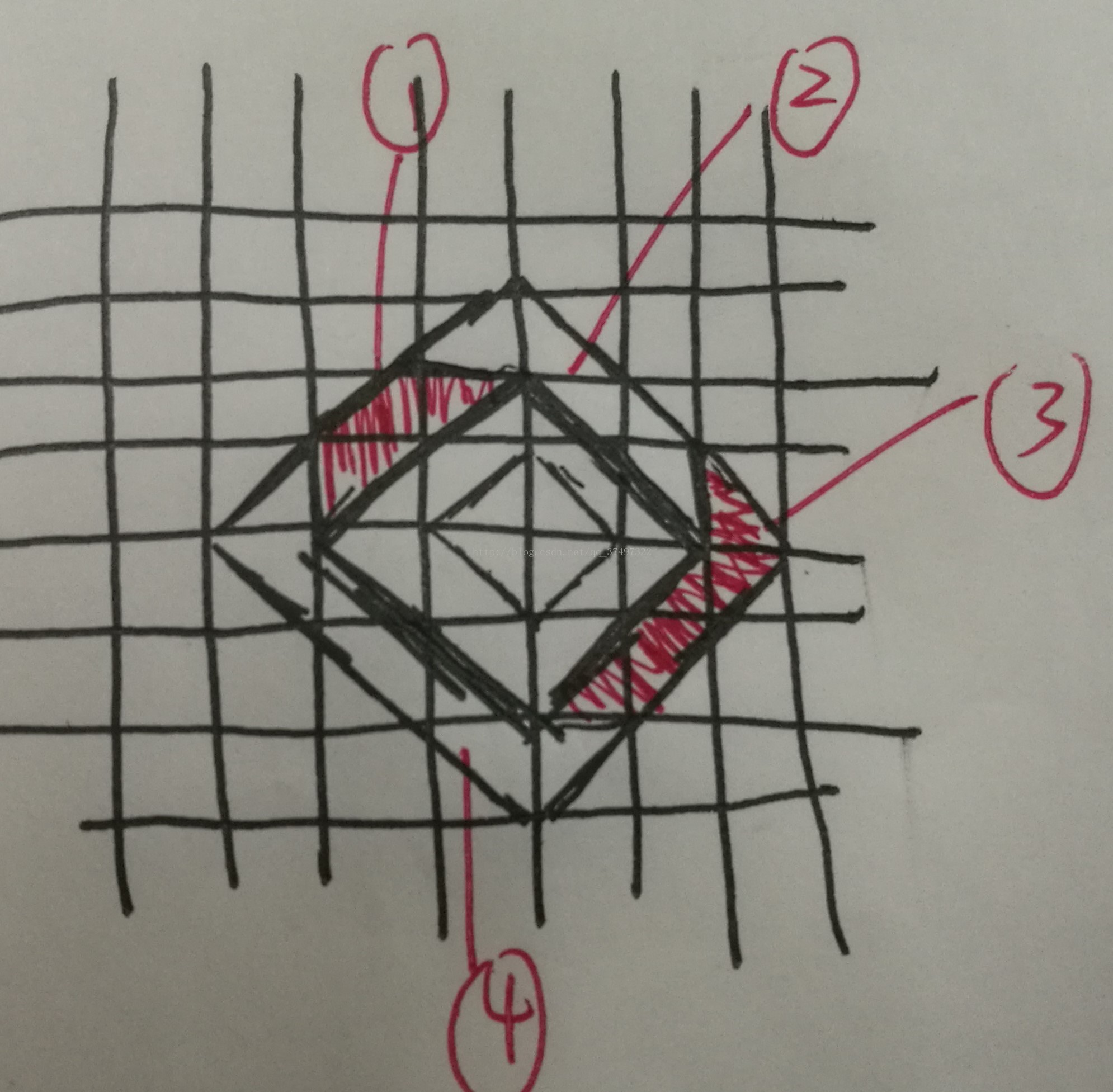
那么逐步添加即可
暂时空着(听队友说是神题,一看是DDP就很有挑战性(bushi))
数位DP裸题不会有人不会吧,不会吧不会吧.jpg(好吧,数位DP忘光的菜鸡就是我,这就回去写)
f[i][j][k]表示i进制下长度为j填到k的方案数,大力DP转移即可。
这也是道神题,如果直接没写过+2^i,-2^i考试的时候肯定做不出来。
我们发现拐弯分为两种,我们发现如果要回到1,那么拐弯的数量必须相同(因题目意思,不算最后一次拐弯),我们只需要统计被两次拐弯框住的路径长度,很容易想到f[i][j][k]表示前i个点选了j个点,左拐弯比右拐弯多了k个(相当于左括号)
那么DP过程中左括号个数必须>=右括号,我们容易发现几种转移
1、不插入任何括号:max(f[i-1][j-1][k],f[i-1][j][k])->f[i][j][k]
2、插入左括号:f[i-1][j-1][k-1]-2*sum[i]+d0->f[i][j][k]
3、插入右括号:f[i-1][j-1][k+1]+2*sum[i]+d0->f[i][j][k]
转就完事了.jpg
这是个圆的反演的裸题,我们发现在大圆小圆公切点反演后,其余的圆都会在两条平行直线内等距排布,这样只要算出第一个圆的圆心,然后往上推每个圆反演回去的反演半径,具体公式可以看这个blog