Code
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 300 Accepted Submission(s): 124
Problem Description
WLD likes playing with codes.One day he is writing a function.Howerver,his computer breaks down because the function is too powerful.He is very sad.Can you help him?
The function:
int calc { int res=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { res+=gcd(a[i],a[j])*(gcd(a[i],a[j])-1); res%=10007; } return res;
}
The function:
int calc { int res=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { res+=gcd(a[i],a[j])*(gcd(a[i],a[j])-1); res%=10007; } return res;
}
Input
There are Multiple Cases.(At MOST 10)
For each case:
The first line contains an integer N(1≤N≤10000).
The next line contains N integers a1,a2,...,aN(1≤ai≤10000).
For each case:
The first line contains an integer N(1≤N≤10000).
The next line contains N integers a1,a2,...,aN(1≤ai≤10000).
Output
For each case:
Print an integer,denoting what the function returns.
Print an integer,denoting what the function returns.
Sample Input
5
1 3 4 2 4
Sample Output
64
Hint
gcd(x,y) means the greatest common divisor of x and y.
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 int F[10000 + 10] , f[10000 + 10]; 5 int num[10000 + 10] ; 6 int prime[10000 + 10] ; 7 int a[10000 + 10] ; 8 int mui[10000 + 10] ; 9 bool vis[10000 + 10] ; 10 int b[10000 + 10] ; 11 int n ; 12 typedef long long ll ; 13 void work_miu () 14 { 15 memset (prime , 0 , sizeof(prime)) ; 16 memset (mui , 0 , sizeof(mui)) ; 17 memset (vis , 0 , sizeof(vis)) ; 18 for (int i = 1 ; i <= 10000 ; i ++) a[i] = i ; 19 for (int i = 2 ; i <= 10000 ; i ++) { 20 for (int j = i ; j <= 10000 ; j += i ) { 21 if (a[j] % i == 0 && ! vis[j] ) { 22 int cnt = 0 ; 23 while (a[j] % i == 0) { 24 a[j] /= i ; 25 cnt ++ ; 26 } 27 if (cnt > 1) { vis[j] = 1 ; mui[j] = 0 ;} 28 else mui[j] ++ ; 29 } 30 } 31 } 32 /* printf ("μ_source: ") ; 33 for (int i = 2 ; i <= 5 ; i ++) printf ("ID %d: %d " , i , mui[i]) ; puts (""); */ 34 mui[1] = 1 ; 35 for (int i = 2 ; i <= 10000 ; i++) { 36 if ( mui[i] ) mui[i] = (int) pow (-1 , mui[i]) ; 37 } 38 } 39 40 void init() { 41 mui[1] = 1; 42 for (int i = 2; i <= 10000; ++ i) { 43 int x = i; 44 int cnt = 0; 45 bool fuck = false; 46 for (int j = 2; j * j <= i; ++ j) { 47 if (x % j == 0) { 48 x /= j; 49 cnt ++; 50 if (x % j == 0) { 51 fuck = true; 52 break; 53 } 54 } 55 } 56 if (x != 1) cnt ++; 57 mui[i] = (cnt & 1) ? -1 : 1; 58 if (fuck) mui[i] = 0; 59 } 60 } 61 62 int main () 63 { 64 // freopen ("a.txt" , "r" , stdin ) ; 65 work_miu () ; 66 //init(); 67 while (~ scanf ("%d", &n) ) { 68 int x ; 69 memset (F , 0 , sizeof(F)) ; 70 memset (num , 0 , sizeof(num) ) ; 71 memset (f , 0 , sizeof(f)) ; 72 for (int i = 0 ; i < n ; i ++) { 73 scanf ("%d" , &b[i]) ; 74 num[ b[i] ] ++ ; 75 } 76 ll sum = 0 ; 77 for (int i = 10000 ; i >= 1 ; i --) { 78 int cnt = 0 ; 79 for (int j = i ; j <= 10000 ; j += i) { 80 cnt += num[j] ; 81 } 82 if (cnt > 0) { 83 F[i] = (cnt * cnt - cnt) / 2 ; 84 for (int j = i ; j <= 10000 ; j += i ) { 85 f[i] += mui[j / i] * F[j] ; 86 } 87 /* if (f[i] != 0) { 88 printf ("ID %d : %d " , i , f[i]) ; 89 }*/ 90 sum += 1ll * f[i] * (i * i - i ) ; 91 } 92 } //puts ("") ; 93 /* puts ("F(X) :") ; 94 for (int i = 1 ; i <= 5 ; i ++) printf ("ID %d: %d " , i , F[i]) ; puts ("") ; 95 printf ("μ: ") ; 96 for (int i = 1 ; i <= 5 ; i ++) printf ("ID %d: %d " , i , mui[i]) ; puts ("") ; 97 printf ("sum=%d " , sum ) ; */ 98 sum *= 2 ; 99 for (int i = 0 ; i < n ; i ++) { 100 sum += b[i] * b[i] - b[i] ; 101 } 102 printf ("%I64d " , sum % 10007) ; 103 } 104 return 0 ; 105 }
我从杰哥那里学到了一种和百度上不同的莫比乌斯反演写法(个人感觉不错):
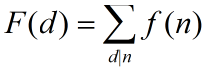
n为d的所有倍数。
则:
μ(1) = 1 ;
k = p1 * p2 * p3 ……*pr(k由r个不同的质数组成)则μ(k) = -1^k ;
其他情况,μ (k) = 0 ;
这道题F(x)指的是x的倍数的对数的个数有多少。
f(x) = 最大公约数为x的多数有多少。
比如:
F(1) = f(1) + f(2) + f(3) + f(4) = 7 + 2 + 0 + 1 = 10
得到F(x)是非常容易的可以统计x的倍数有多少个,比如说=cnt ;
那么此时的F(x) = (cnt * cnt - cnt) / 2 ;(稍微想想就能想通)
Then , it's the time for 。。。。。
