插入排序算法

插入排序算法分为直接插入、折半插入和希尔排序

1.直接插入排序

直接插入排序是一种最简单的排序方法，其基本操作是将一条记录插入到已排好序的有序表中，从而得到一个新的、记录数量增1的有序表。

算法步骤

（1）设待排序的记录存放在数组list[1....n]中，

（2）循环n-1次，每次使用顺序查找法，查找list [ i ] (i=2,...,n)在已排好序的序列list[ 1...i-1 ]中的插入位置，

         然后将list[ i ]插入表长为i-1的有序序列r[ 1...i-1 ],直到将list[ n ]插入表长为n-1的有序序列list[ 1...n-1 ],最后得到一个表长为n的有序序列。

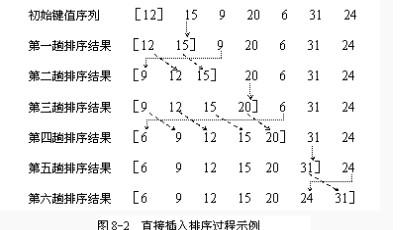
如图：8.2

代码如下

void insertSort(int list[]){
         for(int i=1;i<list.length;i++){
             int j=i;
             int temp=list[j];
             if(list[j]<list[j-1]){
                 while(j>0&&(temp<list[j-1])){
                 list[j]=list[j-1];
                 j--;
              }
                 list[j]=temp;
             }
                
               System.out.println(Arrays.toString(list));   
               
        }      
}         

时间复杂度O(n^2),空间复杂度O(1)

特点:稳定排序，算法简便，且容易实现，也适用于链式存储结构，此算法复杂度较高，不宜采用

2. 折半插入排序

折半插入排序利用查找折半实现，要优于直接插入排序

算法步骤

（1）设待排序的记录存放在数组list[1...n]中；

（2）循环n-1次，每次使用折半查找法，查找list[i]

代码

void BInsertSort(int list[]){
         for(int i=1;i<list.length;++i){
              int temp=list[i];
              int low=0;
              int high=i;
              while(low<=high){
                int mid=(low+high)/2;
                if(temp>list[mid]){
                     low=mid+1;
                 }else{
                       high=mid-1;
                 }
              }
                //将整体数组向后移
            for(int j=i;j>low;j--){
            list[j]=list[j-1];
            }
               list[low]=temp;        
        }  
}

 时间复杂度O(n^2),空间复杂度O(1)

算法特点

（1）稳定排序

（2）因为要进行折半查找，所以只能用于顺序结构，不能用于链式结构

（3）适合初始记录无序、n较大时的情况。

希尔排序

"缩小增量排序"，是插入排序的一种。

算法思想

希尔排序实质上是采用分组插入的方法。先将整个待排序记录列分割成几组，从而减少参与直接插入排序的数据量，对每组分别进行直接插入排序，然后增加每组的数据量，重新分组。这样当经过几次分组排序后，整个序列中的记录”基本有序“时，再对全体记录进行一次直接插入排序。

希尔对记录的分组，不是简单地”逐段分割“，而是将相隔某个”增量“的记录分成一组。

代码

public void sorts(int[] arr){
    int i,j,r,tmp;
    for(r=arr.length/2;r>=1;r=r/2){
        for (i = r; i < arr.length; i++) {
            tmp=arr[i];
            j=i-r;
            //一轮排序
            while(j>=0&&tmp<arr[j]){
                arr[j+r]=arr[j];
                j-=r;
            }
            arr[j+r]=tmp;
        }
        System.out.println(r+":"+Arrays.toString(arr));
    }
}

　时间复杂度O( n 3/2) 空间复杂度为O( 1 )

算法特点

（1）记录跳跃式地移动导致排序方法是不稳定的。

（2）只能用于顺序结构，不能用于链式结构

（3）增量序列可以有各种取法，但应该使增量序列中的值没有除1之外的公因子，并且最后一个增量值必须等于1

（4）记录总的比较次数和移动次数都比直接插入排序要少，n越大时，效果越明显。所以适合初始记录无序、n较大时的情况。