Leetcode OJ: Search in Rotated Sorted Array I/II

对于有序数组进行查找我们可以用二分查找，可以参考我之前写的 Search Insert Position

但如果把这个排序的数组当成一个环，然后做一个旋转操作后再截断，再进行查找又会是什么情况呢？且看下文分解。

Search in Rotated Sorted Array

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

分成了两部分，而且是分别排序的，我们是不是也可以用二分呢？怎么用？先看看以下分析：

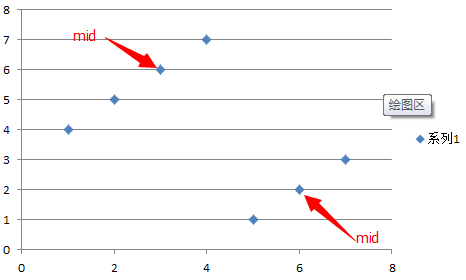
如果二分查找中的mid是落在左侧，则有A[mid] > A[begin] > A[end-1]，否则有A[mid] < A[end - 1] < A[begin]

在我们确定是在哪一侧之后，那问题就变得简单了。

在左侧时，只需要比较target与A[begin]；在右侧时，只需要比较target与A[end]。

具体代码吧：

class Solution {
public:
    int search(int A[], int n, int target) {
        int begin = 0, end = n;
        int mid;
        while (begin < end) {
            mid = begin + ((end - begin) >> 1);
            if (A[mid] == target)
                return mid;
            if (A[mid] > A[begin]) {
                if (A[mid] < target) {
                    begin = mid + 1;
                } else {
                    if (A[begin] < target)
                        end = mid;
                    else if (A[begin] > target)
                        begin = mid + 1;
                    else 
                        return begin;
                }
            } else {
                if (A[mid] > target) {
                    end = mid;
                } else {
                    if (A[end - 1] < target)
                        end = mid;
                    else if (A[end-1] > target)
                        begin = mid + 1;
                    else
                        return end - 1;
                }
            }
        }
        return -1;
    }
};

对于这道题算是完美解决了，细心的同学们可能会发现这题的说明里面特意提到no duplicate，那如果有duplicate又怎样了？于是有了这题的变型：

Search in Rotated Sorted Array II

Follow up for "Search in Rotated Sorted Array":
What if duplicates are allowed?

Would this affect the run-time complexity? How and why?

Write a function to determine if a given target is in the array.

有重复元素又会怎样？我们上面解法的关键在于我们能区分得出mid点是在左侧还是右侧，那如果存在重复的元素呢？且看下图

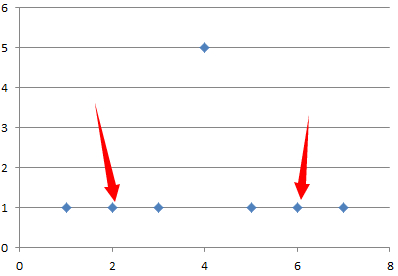
当mid上的点与begin与end-1上的点都相等时，你无法判断是左侧还是右侧！

那怎么解决这个问题呢？我们想想，合并重复元素不就回到之前的问题了？

不过这里我们不用遍历一遍数组然后把重复的元素合并，一方面这样会破坏数组，另一方面，我们还有更高明的办法。

利用好排序的特点，我们只需要begin重复的往后移，end重复的往前移即可。且看代码：

class Solution {
public:
    bool search(int A[], int n, int target) {
        int begin = 0, end = n, mid;
        while (begin < end) {
            // 检测首尾重复的并移动
 7             while (begin < end - 1 && A[begin] == A[begin + 1])
 8                 ++begin;
 9             while (end > begin + 1 && A[end - 1] == A[end - 2])
10                 --end;
            mid = begin + ((end - begin) >> 1);
            if (A[mid] == target)
                return true;
            if (A[mid] > A[begin]) {
                if (A[mid] < target) {
                    begin = mid + 1;
                } else {
                    if (A[begin] > target) {
                        begin = mid + 1;
                    } else if (A[begin] < target) {
                        end = mid;
                    } else {
                        return true;
                    }
                }
            } else {
                if (A[mid] > target) {
                    end = mid;
                } else {
                    if (A[end - 1] > target) {
                        begin = mid + 1;
                    } else if (A[end - 1] < target) {
                        end = mid;
                    } else {
                        return true;
                    }
                }
            }
        }
        return false;
    }
};