每天一套题打卡|河南省第九届ACM/ICPC

A 表达式求值

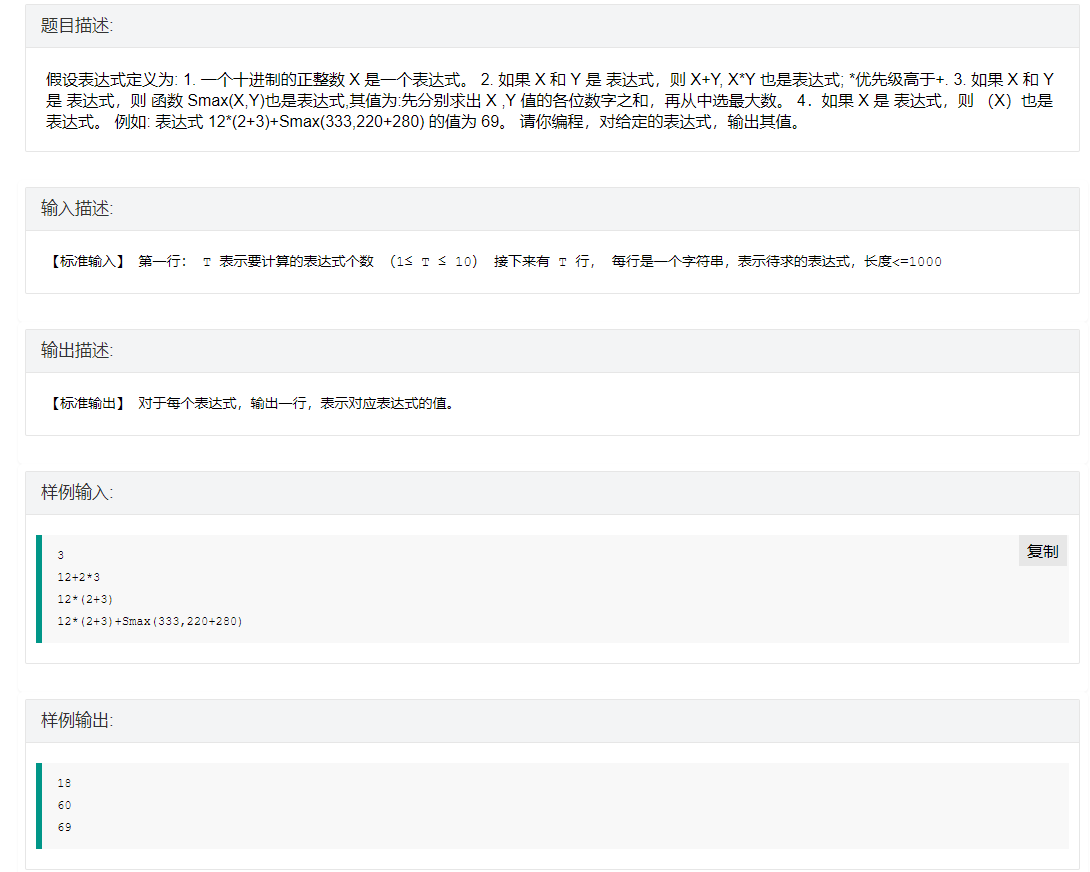
表达式求值：可以用递归求解，也可以用栈模拟，考过多次。

类似题目：NYOJ305，NYOJ35

用栈模拟做法：

#include <stdio.h>
#include <string.h>
#include <stack>
using namespace std;
stack<int> dsta;//数据栈 
stack<char> osta;//字符栈 
char s[1005];
int main()
{
	int T,i,j;
	scanf("%d",&T);
	while(T--)
	{
		scanf("
%s",&s[1]);
		int len=strlen(&s[1]);
		s[0]='('; s[++len]=')';//在给定的表达式两端添加上一对括号 
		for(i=0;i<=len;i++)
		{
			if(s[i]=='(')
				osta.push(s[i]);
			else if(s[i]=='S')
			{
				osta.push('(');//压入一个左括弧 
				i+=3;
			}
			else if(s[i]>='0' && s[i]<='9')
			{
				int v=0;
				while(s[i]>='0' && s[i]<='9')
					v=v*10+(s[i++]-'0');
				i--;
				dsta.push(v);
			}
			else if(s[i]=='+')
			{
				while(osta.top()!='(' && osta.top()!=',')
				{
					int a=dsta.top(); dsta.pop();
					int b=dsta.top(); dsta.pop();
					int c;
					switch(osta.top())
					{
						case '+':c=b+a;break;
						case '*':c=b*a;break;
					}
					dsta.push(c);
					osta.pop();
				}
				osta.push(s[i]);
			}
			else if(s[i]=='*')
			{
				if(osta.top()=='*')
				{
					int a=dsta.top(); dsta.pop();
					int b=dsta.top(); dsta.pop();
					dsta.push(b*a);
					osta.pop();
				}
				osta.push(s[i]);
			}
			else if(s[i]==')' || s[i]==',')//遇到逗号及时求值 
			{ //当遇到 ','时，就把Smax的前半部分表达式的值求出来  
				
				//运算符号 都在这里计算 + - * / smax自定义 
				while(osta.top()!='(')
				{
					int a=dsta.top(); dsta.pop();
					int b=dsta.top(); dsta.pop();
					int c,suma=0,sumb=0;
					switch(osta.top())
					{
						case '+':c=b+a;break;
						case '*':c=b*a;break;
						case ',':{
						//逐位分割求和 
							while(b!=0)
							{
								sumb+=b%10; b/=10;
							}
							while(a!=0)
							{
								suma+=a%10; a/=10;
							}
							c=max(suma,sumb);
							break;
						}
					}
					dsta.push(c);
					osta.pop();
				}
				osta.pop();
				if(s[i]==',')//求完值之后，把逗号压入栈内，以便后半部分Smax表达式的求值 
					osta.push(s[i]);
			}
		}
		printf("%d
",dsta.top());
		dsta.pop();
	}
	return 0;
}

B 宣传墙

状压dp 推状态转移
或者用矩阵快速幂优化

网上代码看不懂。。。

C 信道安全

单源点的最短路修改版，用dijkstra做，初始化dist数组和松弛改一下就可以了。

D 导弹发射

LIS的二分写法，数据量1e5 O(N^2)的会超时。
另外题目中说的 导弹一直在前进，不能以原来的X/Y轴作为坐标轴了，需要坐标变换以两条射线为坐标轴

E 机器设备

我用bfs搜索做的，从原点(0,0)开始搜，每次将与当前点相切的圆心齿轮加入到队列，这里的相切意思是:两个圆心距离等于两个圆半径和

F Decimal integer conversion

题意：给一个十进制数 的二进制数 和一个 三进制数，其中各有一位是错的，求正确的十进制数
枚举一下就可以了，二进制和三进制 转成10进制后出现相同的数就是答案

G Prototypes analyze

一个二叉搜索树，问形状有多少个。
明天看题解，学会建树吧......

jBST二叉搜索树的创建 参考博客：https://blog.csdn.net/stpeace/article/details/9067029
nyoj1278 题解参考博客：https://blog.csdn.net/baidu_35643793/article/details/70792326

这道题 题意就是 判断二叉排序树的形状有多少个不一样。
首先 建树 就用上面的板子。
然后就是 判断形状：只需要各个位置是否对应一致有值就行了（如果一颗树在这个地方是空的，那么另一颗树要想与它形状相同，这个地方也必须是空的）

//BST二叉搜索树；
#include<cstdio>
#include<iostream>
using namespace std;
 
int flag;
 
typedef struct Node
{
    int key;
    struct Node *lChild,*rChild;
} Node,*BST;
 
bool BSTInsert(Node * &p,int element)
{
    if(p==NULL)
    {
        p=new Node;
        p->key=element;
        p->lChild=p->rChild=NULL;
        return true;
    }
    if(element==p->key)
        return false;
    if(element<p->key)
        return BSTInsert(p->lChild,element);
    return BSTInsert(p->rChild,element);
}
 
void judge(BST T1,BST T2)  //判断形状；
{
    if(T1==NULL&&T2==NULL)
        return;
    else if(T1&&T2)
    {
        judge(T1->lChild,T2->lChild);
        judge(T1->rChild,T2->rChild);
    }
    else
        flag=0;
}
 
int main()
{
    int t,n,k,x;
    BST tree[55];
 
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&k);
        for(int i=0; i<n; i++)  
        {
            BST T=NULL; 
            for(int j=0; j<k; j++)  //建树；
            {
                scanf("%d",&x);
                BSTInsert(T,x);
            }
            tree[i]=T;
        }
 
        //找形状种类数；
        int ans=0;
        for(int i=0; i<n; i++)
        {
            int flog=1;
            for(int j=i+1; j<n; j++)
            {
                flag=1;
                judge(tree[i],tree[j]);
                if(flag)
                {
                    flog=0;
                    break;
                }
            }
            if(flog)
                ++ans;
        }
        printf("%d
",ans);
    }
    return 0;
}