Description
给你两个整数N和K,要求你输出N!的K进制的位数。
Input
有多组输入数据,每组输入数据各一行,每行两个数——N,K
Output
每行一个数为输出结果
Sample Input
2 5
2 10
10 10
100 200
Sample Output
1
1
7
69
对于100%的数据,有2≤N≤2^31, 2≤K≤200,数据组数T≤200。
题解
用Stirling公式求近似值
位数=logk(n!)+1
≈ logk(sqrt(2πn)*(n/e)^n)+1
= logk( sqrt(2πn))+log[(n/e)^n]+1
=1/2*logk( 2πn)+nlog(n/e)+1
=0.5*logk ( 2πn)+nlog(n/e)+1
=0.5*logk ( 2πn)+nlog(n)-nlog(e)+1
PS:pi=acos(-1.0),e=exp(1)
PS2:eps的存在是为了防止n=2,k=2这样刚好的情况出现,这个时候向上取整要多取1位
斯特林公式是求解n!的近似解,对于较大的n数值是十分准确的。
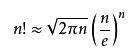
所以可以通过数学方法解决。
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<cstdio> 5 #include<algorithm> 6 7 #define ll long long 8 using namespace std; 9 const double eps=0.00000000001; 10 const double pai=3.14159265359; 11 const double e=exp(1); 12 13 int n,k; 14 15 int main() 16 { 17 freopen("fzy.in","r",stdin); 18 freopen("fzy.out","w",stdout); 19 while(~scanf("%d%d",&n,&k)) 20 { 21 if (n<=1000) 22 { 23 double ans=0; 24 for (int i=1;i<=n;i++) 25 ans+=log(i); 26 ans/=log(k); 27 int res=ceil(ans+eps); 28 printf("%d ",res); 29 } 30 else 31 { 32 double res=(log(sqrt(2*pai*n))+n*log(n/e))/log(k); 33 ll ans=ceil(res-eps); 34 printf("%lld ",ans); 35 } 36 } 37 }
对了,c++小数处理的时候会有精度损失的问题,所以需要适当加上一个小数