动态规划 Dynamic Programming
- 理查德·贝尔曼(Richard Bellman)在1957年提出了动态规划(Dynamic Programming, 即 DP)一词
- 通过将解决方案与包含一般子问题的子问题组合来解决问题
- DP 与 分治之间的不同点:
- 使用分而治之解决这些问题的效率很低, 因为相同的子问题必须多次解决(暂时缺乏具体的例子, 需要多做题目)
- DP 将解决每个问题一次, 并将其答案存储在表格中以备将来参考
硬币找零问题
- 目标: 给定硬币的面值, 例如, 1, 5, 10, 25, 100, 设计一种使用最少数量的硬币向客户付款的方法
- 收银员算法(Cashier's algorithm): 在每次迭代中, 添加不会使我们超过要支付的金额的最大值的硬币
- 例子: 33 美分(33 cents) --> 一个 25 美分 + 一个 5 美分 + 三个 1 美分
收银员算法
将 n 个硬币按照面值进行排序, 使得:
[c_1 < c_2 < ... < c_n
]
(S leftarrow empty)
WHILE x > 0
k (leftarrow) largest coin denomination (c_k) such that (c_k leq x)(最大硬币面值 (c_k) 使得 (c_k leq x))
IF no such k, RETURN "no solution"
ELSE
(x leftarrow x - c_k)
(S leftarrow S cup { k })
RETURN S
找零(Coin Changing)
这个贪婪算法 -- 收银员算法是最优的吗?
定理
收银员算法对于美国硬币来说是最佳的算法, 即这个贪婪算法可以求出最优解(U.S. coins -- 1, 5, 10, 25, 100).
可以根据 x 进行归纳证明(存疑, 待补充, 算法本身肯定是正确的).
其他的情况
- 收银员算法在其他的情况下可能并不奏效
- 考虑美国的邮费: 1, 10, 21, 34, 70, 100, 350, 1225, 1500(这些都是美国邮费的面值, 并且可能每年都会变)
- 使用收银员算法: 140 美分 = 100 + 34 + 1 + 1 + 1 + 1 + 1 + 1
- 而最佳的做法: 140c(即 140 美分) = 70 + 70
- 在某些情况下, 甚至可能无法找到可行的解决方案
动态规划
- 为了对 n 美分进行找零, 我们将首先弄清楚如何对每个值 (x < n) 进行找零
- 我们可以从解决方案中构建出更小的值
- 令 (C[n]) 为给 n 美分找零所需的最少的硬币数量
- 令 (x) 为最优解中使用的第一个硬币的值
- 然后 (C[n] = 1 + C[n - x])
- 问题的关键是: 我们不知道 x 的值
动态规划算法
我们将尝试所有可能的 (x) 值, 并取最小值
[C[n] = left{egin{matrix}
min_{i:d_i leq n}left{ C[n - d_i] + 1
ight} qquad if n > 0 & \
0 qquad qquad qquad qquad qquad qquad if n = 0& \
end{matrix}
ight.
]
Change 代码
伪码描述
int Change(int n)
{
if (n < 0>)
return INFTY;
else if (n == 0)
return 0;
return 1 + min(Change(n - d1), Change(n - d2), Change(n - d3));
}
图解
(n = 12, d_1 = 1, d_2 = 3, d_3 = 7)
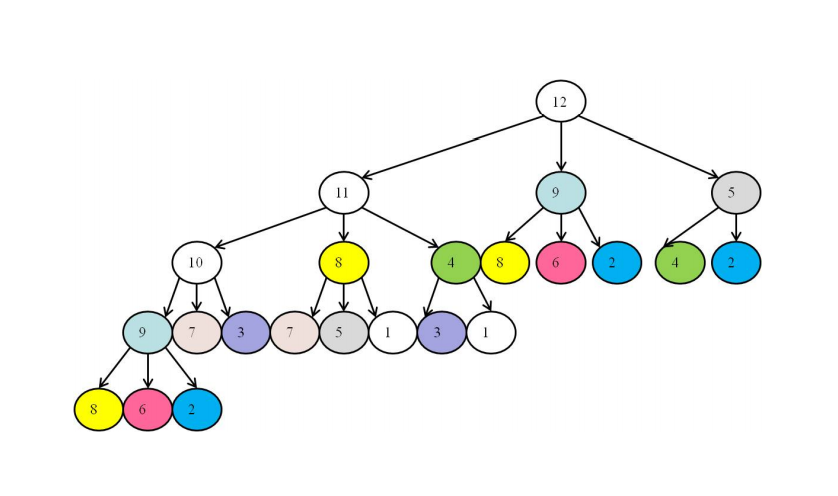
这棵树的根节点是我们要求解的 n, 然后 n 分别减去 (d_1, d_2, d_3) 得到其三个子节点, 然后从左到右依次递归分解这 3 个子节点, 然后以此类推.
最后求解出来的找零所需的最少的硬币的数目是 4, 根据上面的树可以发现, 具体的分法不是唯一的.
动态规划的要素
DP 用于解决具有以下特征的问题:
- 最优子结构(最优原理): 问题的最优解决方案中包括子问题的最优解决方案
- 子问题重叠: 在某些地方, 我们多次解决同一子问题
动态规划的步骤
- 表征最佳子结构
- 递归定义最佳解决方案的值
- 自下而上计算值
- (如果需要)构建最佳解决方案
记忆化(Memoization)
- 记忆化是处理重叠子问题的一种方法
- 计算出子问题的解决方案后, 将其存储在表中
- 后续调用
- 可以修改递归算法以使用记忆化
Change()有许多重复的工作, 使用一个表来使得算法的时间复杂度变为 (O(nk))
DP_Change(n)
伪码描述
int DP_Change(int n)
{
int tmp, i, j;
for(i = 1, C[0] = 0; i<= n; i++)
{
tmp = INFTY;
for(j = 0; j < ; j++)
if (d[j] <= i && C[i - d[j]] + 1 < tmp)
tmp = C[i - d[j]] + 1; // 更新最小值
C[i] = tmp;
}
return tmp; // 最后返回的即 C[n]
}
这个算法和上面的递归相反, 是从底向上进行构建的.
从底向上构建
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (C[n]) | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | 2 | 3 | 2 | 3 | 4 |
| (d_1) | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 0 | 1 | 2 | 0 | 1 | 2 |
| (d_2) | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 0 | 1 | 1 | 1 |
| (d_3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
动态规划 VS 贪婪算法
- DP 适合具有以下特征的问题:
- 最优子结构: 问题的最优解决方案包括子问题的最优解决方案
- 子问题重叠: 子问题总数很少, 每个子问题都有许多重复出现的实例
- 自下而上, 建立一张已解决的子问题表, 用于解决较大的子问题
- 贪婪算法是自上而下的, 动态规划可能是过大的(overkill); 贪婪算法往往更容易编码.