题面
Description:
一棵(n)个点的树,每个点的初始权值为(1)。对于这棵树有(q)个操作,每个操作为以下四种操作之一:
+ u v c:将(u)到(v)的路径上的点的权值都加上自然数(c);- u1 v1 u2 v2:将树中原有的边(u1-v1)删除,加入一条新边(u2-v2),保证操作完之后仍然是一棵树;* u v c:将(u)到(v)的路径上的点的权值都乘上自然数(c);/ u v:询问(u)到(v)的路径上的点的权值和,求出答案对于(51061)的余数。
Input
第一行两个整数(n,q)
接下来(n-1)行每行两个正整数(u,v),描述这棵树
接下来(q)行,每行描述一个操作
Output
对于每个/对应的答案输出一行
Sample Input
3 2
1 2
2 3
* 1 3 4
/ 1 1
Sample Output
4
HINT
100%的数据保证,$$1le n,qle 100000,1le u,v,u1,v1,u2,v2le n,0le cle 100001$$
Link-cut Tree 的作用&思想
-
作用:类似于动态树链剖分(可以修改点、边)
-
思想:用链的思想,把树剖为多个伸展树
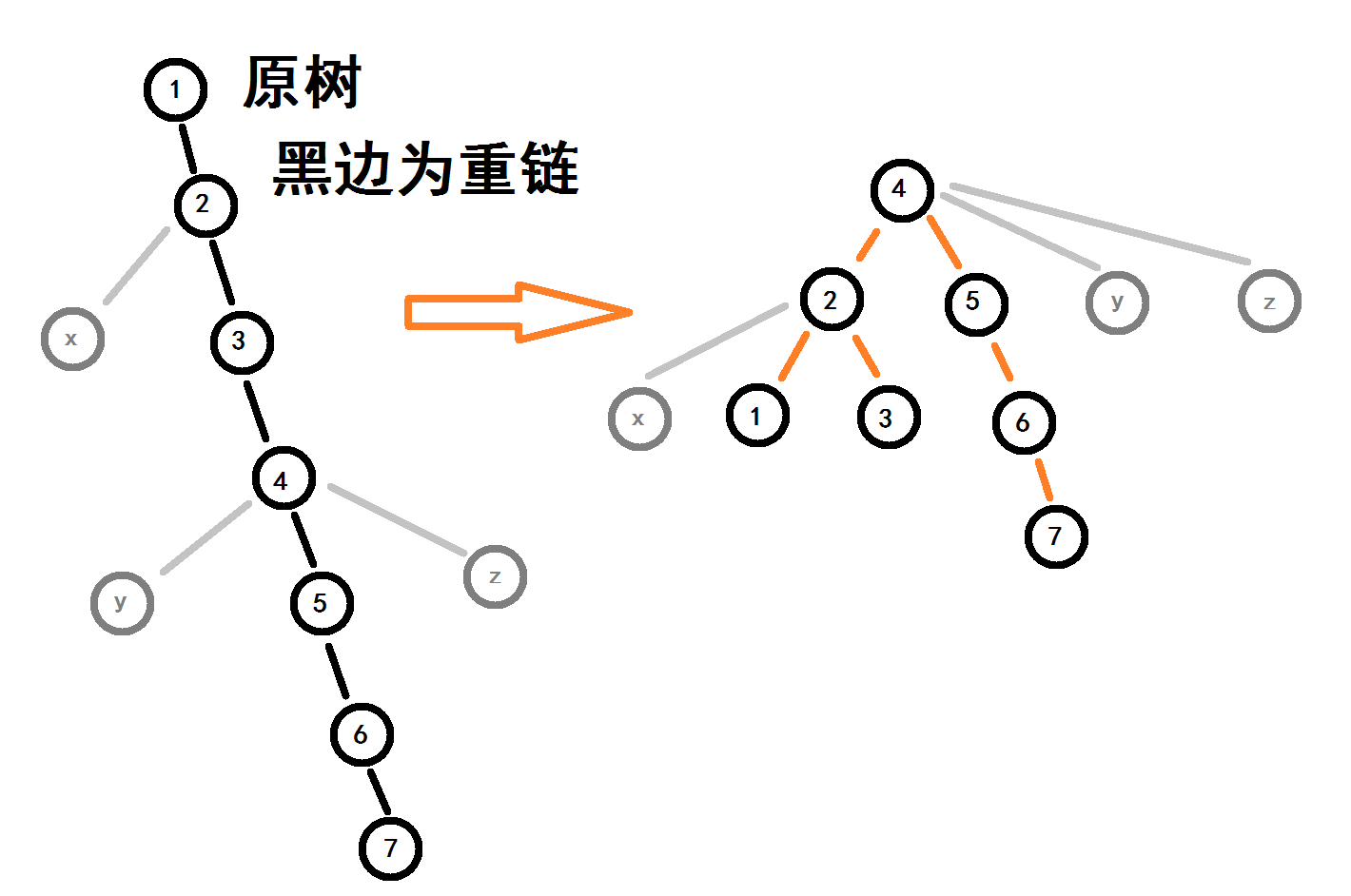
树与树之间只保存父关系,不保存子关系。
树链剖分把树分成若干条重链,对于每条重链,用线段树来维护信息。利用各线段树的信息来得到答案。
Link-cut Tree 的基本操作
1.access(u):把u到根节点变成一条链
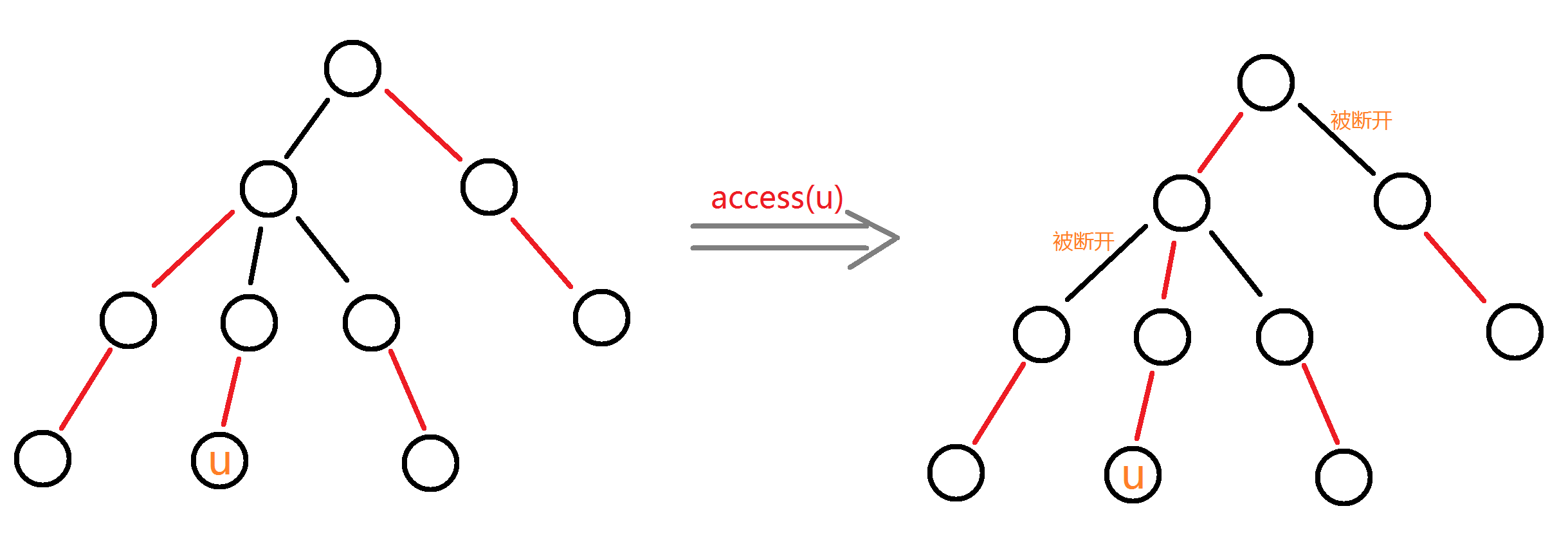
u是当前点,v是前驱
其实就是一层一层往上爬,每次顺带修改链上的儿子
void access(int u){
for(int v=0;u;v=u,u=fa[u]){
splay(u);
ch[u][1]=v;
pushup(u);
}
}
2.makeroot(u):把u变成根
access+splay后,u已经是根,可splay的路径上需要进行父子反向,其他的没有影响,因此要进行翻转
void makeroot(int u){
access(u);
splay(u);
reverse(u);
}
3.cut(u,v):切断u,v之间的连接
我们先makeroot(u)+access(v)+splay(v)
由于u和v同在一棵Splay中且u一定是v的父亲,所以Splay中v的左儿子一定是u,断开即可。
void cut(int a,int b){
makeroot(a);
access(b);
splay(b);
ch[b][0]=0;
fa[a]=0;
pushup(b);
}
4.link(u,v):连接u,v
把u变成根,这时u没有父亲,就可以安心连接了。再把其父亲设为v,就实现了连接。
void link(int a,int b){
makeroot(a);
fa[a]=b;
}
5.isconnect(u,v):检测u,v是否连接
我们先makeroot(u)+access(v)+splay(v)
如果u和v不在同一棵LCT中,执行makeroot(u)后,u的父亲应该为空(他是根)
除非a和b在同一棵树中,在access(v)+splay(v)后,u与v应该在同一棵Splay中,既然v是根,那么u就不是根,即u一定有一个父亲存在。
bool isconnect(int a,int b){
if(a==b) return true;
makeroot(a);
access(b);
splay(b);
return fa[a];
}
代码
注意有多个修改中懒标的特殊处理方式。
#include<iostream>
#include<cstdio>
using namespace std;
int ch[100001][2],fa[100001],siz[100001],lazr[100001],cnt,n,q;
unsigned num[100001],tot[100001],lazp[100001],lazc[100001],mod=51061;
inline unsigned rd(){
unsigned re=0;
char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
re=re*10+ch-'0';
ch=getchar();
}
return re;
}
inline bool isroot(int bt){return ch[fa[bt]][0]!=bt&&ch[fa[bt]][1]!=bt;}
inline int drct(int bt){return ch[fa[bt]][1]==bt;}
inline void pushup(int bt){siz[bt]=siz[ch[bt][0]]+siz[ch[bt][1]]+1;tot[bt]=((tot[ch[bt][0]]+num[bt])%mod+tot[ch[bt][1]])%mod;}
inline void reverse(int bt){swap(ch[bt][0],ch[bt][1]);lazr[bt]^=1;}
inline void add(int bt,unsigned c){num[bt]=(num[bt]+c)%mod;tot[bt]=(tot[bt]+siz[bt]*c)%mod;lazp[bt]=(lazp[bt]+c)%mod;}
inline void times(int bt,unsigned c){num[bt]=(num[bt]*c)%mod;tot[bt]=(tot[bt]*c)%mod;lazc[bt]=(lazc[bt]*c)%mod;lazp[bt]=(lazp[bt]*c)%mod;}
inline void pd(int bt){
if(lazr[bt]){
if(ch[bt][0])reverse(ch[bt][0]);
if(ch[bt][1])reverse(ch[bt][1]);
lazr[bt]=0;
}
if(lazp[bt]){
if(ch[bt][0])add(ch[bt][0],lazp[bt]);
if(ch[bt][1])add(ch[bt][1],lazp[bt]);
lazp[bt]=0;
}
if(lazc[bt]!=1){
if(ch[bt][0])times(ch[bt][0],lazc[bt]);
if(ch[bt][1])times(ch[bt][1],lazc[bt]);
lazc[bt]=1;
}
}
inline void pushdown(int u){
if(!isroot(u))pushdown(fa[u]);
pd(u);
}
inline void rotate(int u){
int f=fa[u],g=fa[f],c=drct(u);
if(!isroot(f))ch[g][drct(f)]=u;
fa[u]=g;
ch[f][c]=ch[u][c^1];
if(ch[f][c])fa[ch[f][c]]=f;
ch[u][c^1]=f;
fa[f]=u;
pushup(f);
pushup(u);
}
void splay(int u){
pushdown(u);
while(!isroot(u)){
if(!isroot(fa[u]))rotate(drct(fa[u])==drct(u)?fa[u]:u);
rotate(u);
}
}
void access(int u){
for(int v=0;u;v=u,u=fa[u]){
splay(u);
ch[u][1]=v;
pushup(u);
}
}
void makeroot(int u){
access(u);
splay(u);
reverse(u);
}
void link(int a,int b){
makeroot(a);
fa[a]=b;
}
void cut(int a,int b){
makeroot(a);
access(b);
splay(b);
ch[b][0]=0;
fa[a]=0;
pushup(b);
}
void makeline(int u,int v){
makeroot(u);
access(v);
splay(v);
}
int main(){
n=rd();
q=rd();
for(int i=1;i<=n;i++)lazc[i]=num[i]=tot[i]=siz[i]=1;
for(int i=1;i<n;i++){
int u=rd(),v=rd();
link(u,v);
}
makeroot(1);
for(int i=1;i<=q;i++){
char cha[5];
scanf("%s",cha);
int u=rd(),v=rd();
if(cha[0]=='+'){
unsigned c=rd();
makeline(u,v);
add(v,c);
}else if(cha[0]=='-'){
int u2=rd(),v2=rd();
cut(u,v);
link(u2,v2);
}else if(cha[0]=='*'){
unsigned c=rd();
makeline(u,v);
times(v,c);
}else if(cha[0]=='/'){
makeline(u,v);
printf("%u
",tot[v]);
}
}
}




