三维绘图函数

三维绘制工具

函数view



实例:三维螺旋线
>> t=0:pi/50:10*pi; plot3(sin(t),cos(t),t) grid %添加网格
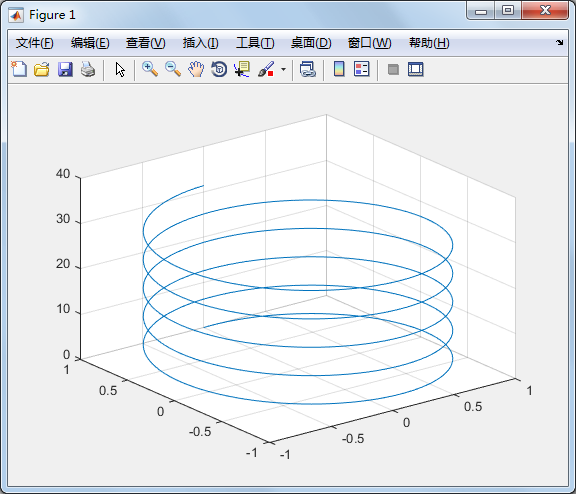
plot3可以画出空间中的曲线
>> t=linspace(0,20*pi, 501); plot3(t.*sin(t), t.*cos(t), t); %注意用点乘 .*
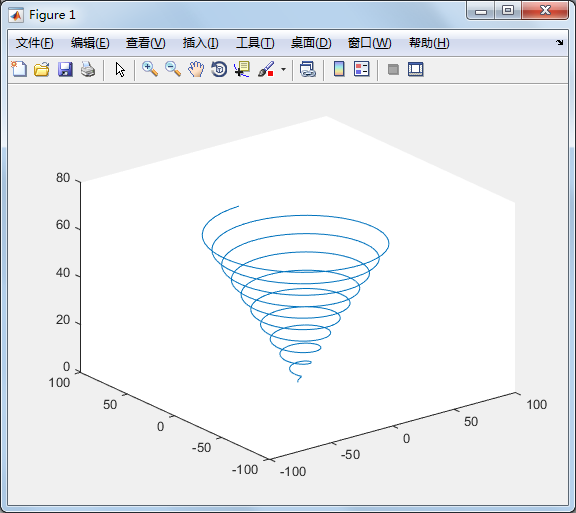
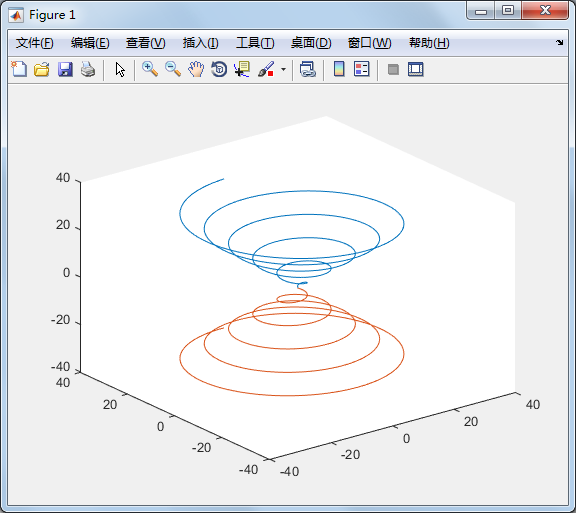
也可以同时画出两条空间中的曲线
>> t=linspace(0,10*pi,501); >> plot3(t.*sin(t),t.*cos(t),t,t.*sin(t),t.*cos(t),-t);
正弦曲线图
x=linspace(0,3*pi); % 0 到 3pi 间100 个数据点 z1=sin(x); z2=sin(2*x); z3=sin(3*x); y1=zeros(100); % 含有100 个数据的 0 数组 y3=zeros(100); y2=y3/2; plot3(x,y1,z1,x,y2,z2,x,y3,z3);

立体网状图

实例:
>> x=linspace(-2, 2, 25); %在x轴上取25点 y=linspace(-2, 2, 25); %在y轴上取25点 [xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵 zz=xx.*exp(-xx.^2-yy.^2); %计算函数值,zz也是21x21的矩阵 mesh(xx, yy, zz); %画出立体网状图
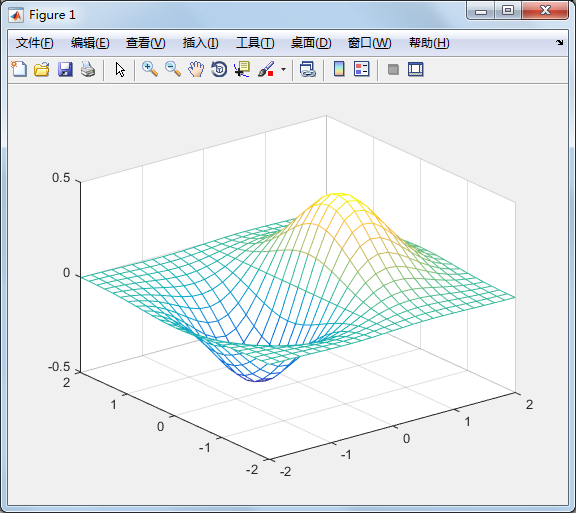
曲面图

>> x=linspace(-2, 2, 25); %在x轴上取25点 y=linspace(-2, 2, 25); %在y轴上取25点 [xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵 zz=xx.*exp(-xx.^2-yy.^2); %计算函数值,zz也是21x21的矩阵 surf(xx, yy, zz);%画出立体曲面图

peaks函数

>> z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ... - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ... - 1/3*exp(-(x+1).^2 - y.^2); >> peaks z
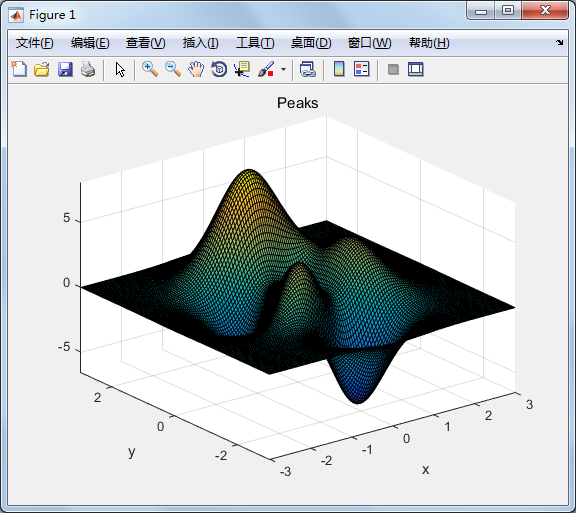
也可以对peaks函数取点,再以各种不同的方法进行绘图
meshz 可将曲面加上围裙
[x,y,z]=peaks;
meshz(x,y,z);
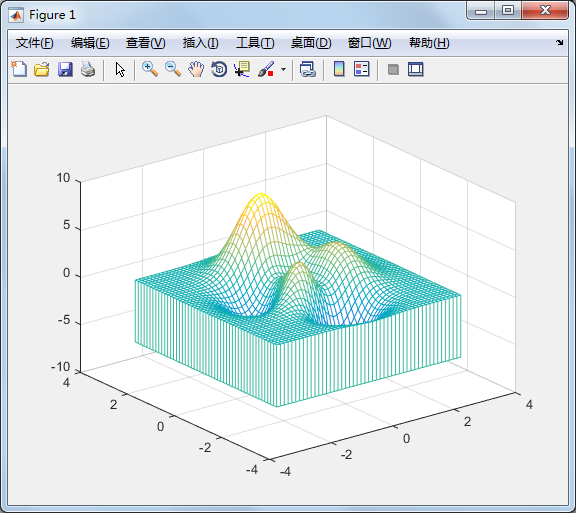
waterfall 可在x 方向或y 方向产生水流效果:
[x,y,z]=peaks;
waterfall(x,y,z);
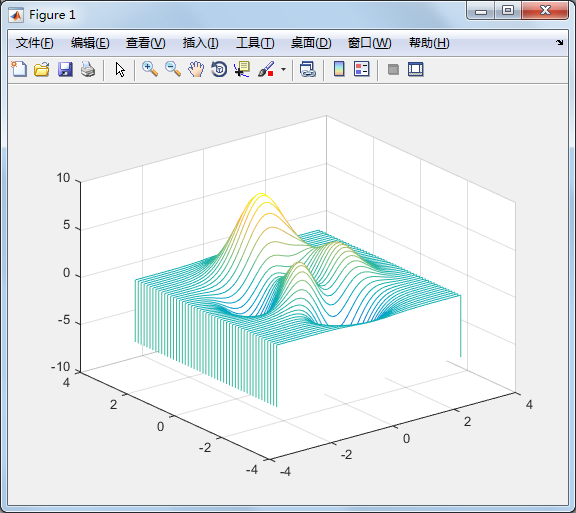
产生在y方向的水流效果:
[x,y,z]=peaks; waterfall(x',y',z');
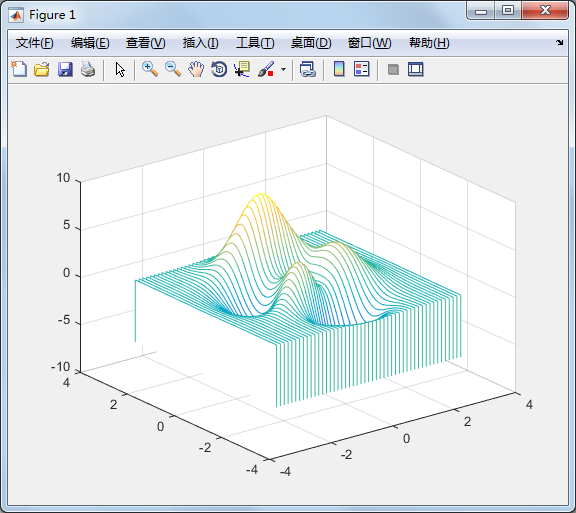
meshc 同时画出网状图与等高线:
[x,y,z]=peaks;
meshc(x,y,z);
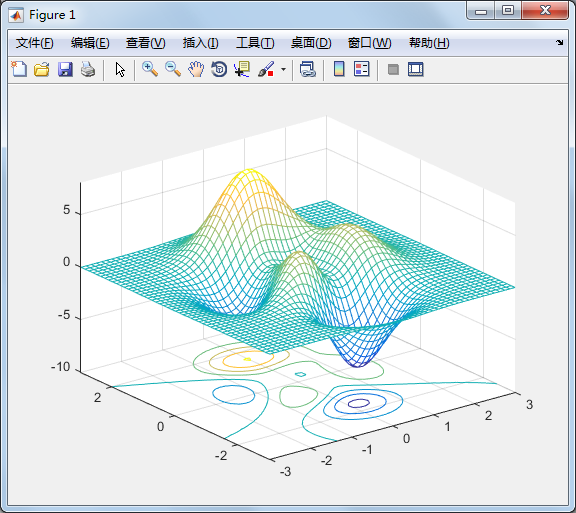
surfc 同时画出曲面图与等高线:
[x,y,z]=peaks;
surfc(x,y,z);

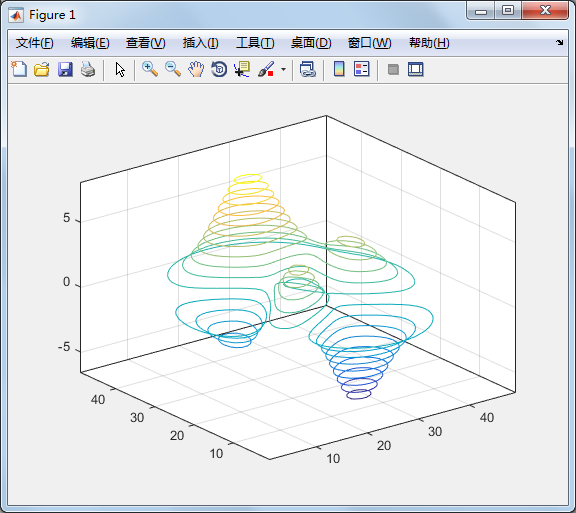
contour3 画出曲面在三度空间中的等高线
contour3(peaks, 20);
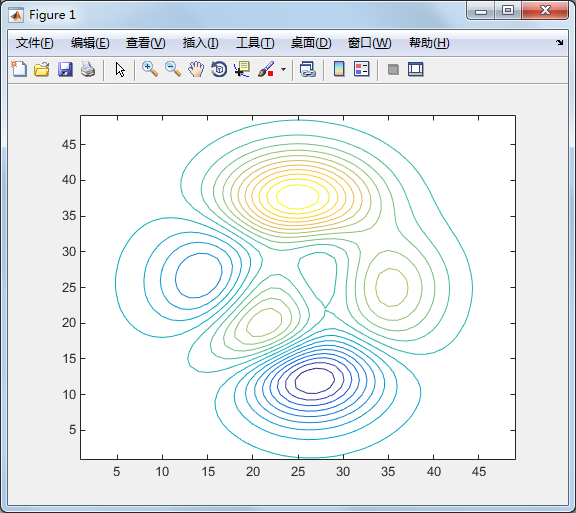
contour 画出曲面等高线在XY 平面的投影
contour(peaks, 20);
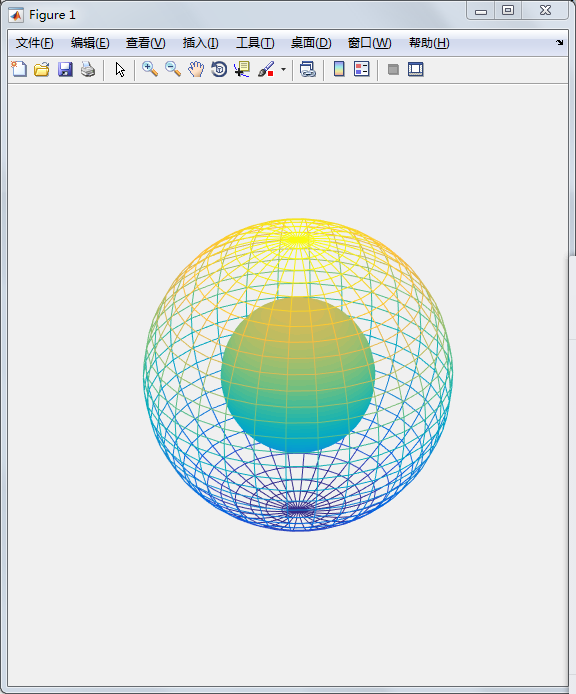
剔透玲珑球
[X0,Y0,Z0]=sphere(30); %产生单位球面的三维坐标 X=2*X0;Y=2*Y0;Z=2*Z0; %产生半径为2 的球面的三维坐标 surf(X0,Y0,Z0); %画单位球面 shading interp %采用插补明暗处理 hold on; mesh(X,Y,Z);hold off %画外球面 hidden off %产生透视效果 axis off %不显示坐标轴
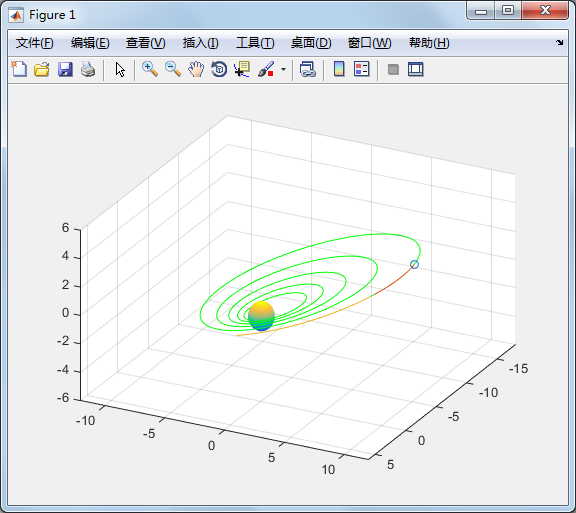
动态图形动画效果——彗星状轨迹图
R0=1; %以地球半径为一个单位 a=12*R0;b=9*R0;T0=2*pi; %T0是轨道周期 T=5*T0;dt=pi/100;t=[0:dt:T]'; f=sqrt(a^2-b^2); %地球与另一焦点的距离 th=12.5*pi/180; %卫星轨道与x-y平面的倾角 E=exp(-t/20); %轨道收缩率 x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t)); plot3(x,y,z,'g') %画全程轨线 [X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z; %获得单位球坐标 grid on,hold on,surf(X,Y,Z),shading interp %画地球 x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0; axis([x1 x2 y1 y2 z1 z2]) %确定坐标范围 view([117 37]),comet3(x,y,z,0.02),hold off %设视角、画运动轨线