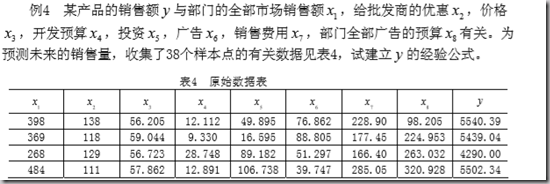
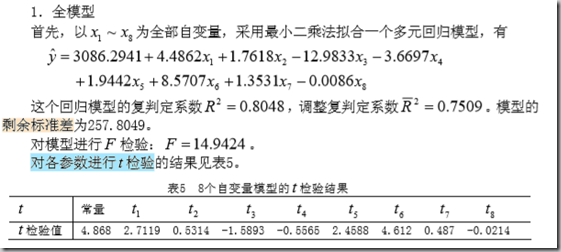
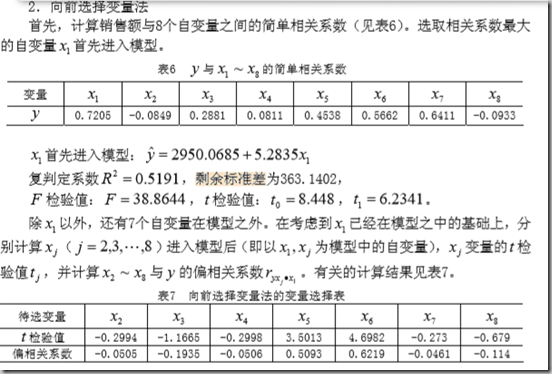
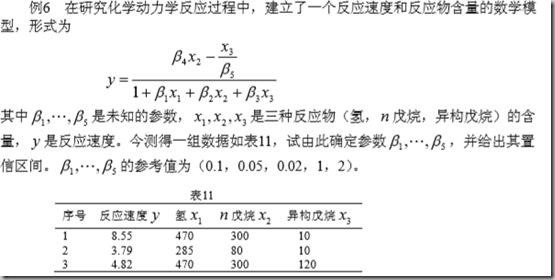
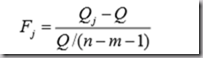2. 回归分析
回归分析与曲线拟合区分。
曲线拟合是,根据得到的若干有关变量的一组数据,寻找因变量与(一个或几个)自变量之间的一个函数,使这个函数对那组数据拟合得好。通常,函数的形式可以由经验、先验知识或对数据的直观观察决定,要 作的工作是由数据用小二乘法计算函数中的待定系数。
但是,从数理统计的观点看,这里涉及的都是随机变量,我们根据一个样本计算出的那些系数,只是它们的一个(点)估计,应该对它们作区间估计或假设检验,如果置信区间太大,甚至包含了零点,那么系数的估计值是没有多大意义的。可以用方差分析 方法对模型的误差进行分析,对拟合的优劣给出评价。
简而言之:回归分析就是对拟合问题作的统计分析。
1)必备的知识(重点)
数理统计样本方差,样本均值、期望、方差、k阶矩、k阶中心距的概念。
数据的标准化处理:
2)一元线性回归
1. 用最小二乘法求出回归系数(即回归方程的待定系数)。
2. 拟合效果分析
看以下几个标度:
a. 残差的样本方差(标准差)
拟合方程求出的y与真实的y之差叫残差。求这个残差的方差。越小越精确。
b. 判定系数(拟合优度)
建立一元线性回归模型的目的, 就是试图以x 的线性函数来解释 y 的变异。
->求样本的y的方差,记做SST:
->求回归方程求出的y估的方差,记做SSR:
->SSE = SST - SSR,即为残差平方和:
->可以看到: SSE = SST - SSR; dfT = dfR + dfE;
从上式可以看出,y 的变异是由两方面的原因引起的;一是由于x 的取值不同,而 给 y 带来的系统性变异;另一个是由除 x以外的其它因素的影响。
也就是说:
从而,可以指定判定如下:
定义一个测量标准来说明回归方程对原始数据的拟合程度,这就是所谓 的判定系数,有些文献上也称之为拟合优度。
3. 显著性检验:回归方程的假设检验
一元线性回归,我们假设的是y和x是线性关系,但这个线性关系的假定是否靠谱,还要进行显著性检验。
换句话说,β1系数就是线性程度,若β1趋向0,则线性关系不显著。
假设检验:
H0:β1 = 0;
H1:β1 ≠ 0;
传统检验,若接受H0,则线性关系不显著。
一般地,回归方程的假设检验包括两个方面:一个是对模型的检验,即检验自变量 与因变量之间的关系能否用一个线性模型来表示,这是由F 检验来完成的;另一个检 验是关于回归参数的检验,即当模型检验通过后,还要具体检验每一个自变量对因变量 的影响程度是否显著。这就是下面要讨论的t检验。在一元线性分析中,由于自变量的 个数只有一个,这两种检验是统一的,它们的效果完全是等价的。但是,在多元线性回 归分析中,这两个检验的意义是不同的。从逻辑上说,一般常在F 检验通过后,再进 一步进行t检验
4. 回归系数的显著性检验
回归参数的检验是考察每一个自变量对因变量的影响是否显著。换句话说,就是要 检验每一个总体参数是否显著不为零。
也就是说,若某一个回归系数接近0,那么这个对应的变量对y的影响就是不显著的。我们对每一个回归系数进行是否等于0的假设检验,得到显著性分析。
对于每一个βi,检验:
H0:βi = 0;
H1:βi ≠ 0;
决策为:
5. 利用回归方程进行预测
这里有点估计、区间估计。
点预测代数即可。
区间预测比较复杂,用到需要查阅。
===
总结回归分析的步骤:
step1:
给定回归形式(这由经验、先验等得到),以最小二乘拟合等方法得到回归方程的系数
step2:拟合效果分析:这一步检验拟合的效果如何,即回归方程能否比较好的解释y随x的变化。有两个指标需要计算和检验。
a. 检验残差的样本方差。
求残差样本均值,对每一对数据得到的残差(ei = yi - yi估)进而求样本方差MSE。MSE应当小,这样残差变化不大,反应我们的映射是可以的。
b. 检验判定系数:拟合优度检验
仅仅得到残差变化不大,是说明在拟合点处做的可以。但我们还要直到拟合的精度怎么样?也就是说,仅仅知道残差变化不大是不够的,还要具体的知道拟合的精度。
求SST 是原始数据yi的总变异平方和。
求SSR 是拟合数据yi估的总变异平方和。
SSE = SST –SSR 是残差平方和。
这说明。SST = SSE + SSR。原始数据的变异由两部分解释:一个是我们的拟合,即来自x的影响,另一个是残差,即来自随机误差。
判定系数R^2 = SSR /SST。即来自x对y的变异影响占y总变异影响的比重。
R^2应接近于1.
STEP3:显著性检验:上面的假设是给定了回归方程形式,但这个形式靠谱不靠谱还是需要检验的。分两步,F检验和t检验。
a. F检验
检验回归模型的方程形式是否靠谱。
求SSR,SSE。F = (SSR/1)/ (SSE/(n-2)) 服从F(1,n-2)分布。
记:yi关于xi的总体回归系数是βi。
检验H0 :βi= 0;
根据F检验。若拒绝H0,则通过了F检验,也就是说拥有给定回归关系是显著的。
b. t检验
给定回归方程形式中有许多的回归系数,这些系数反映了各自对应的变量x对y的影响如何。但这个影响是否是显著的 呢?就是说若回归系数近似为0,则该变量其实对目标y没有什么影响。这里需要t检验,检验每一个回归系数。
对系数构造统计量(查阅)服从t(n-2),检验:
H0: βi = 0
检验若落在拒绝域,则拒绝H0,通过了t检验。
综上,检验结束。
MATLAB中提供的几种回归形式:
(多元线性、高次(多元二次、一元多项式))
MATLAB中的多元线性回归:
形式:
函数:b = regress(Y,X)
param:
Y,X按照下列排列:
return:
返回相应形式的系数β。
函数:[b,bint,r,rint,stats]=regress(Y,X,alpha)
param:
这里指定检验的显著性水平alpha。
return:
b和bint是系数的估计值以及1-alpha置信区间。
r和rint是残差(向量)以及其置信区间。
stats:是四个量,用于检验的统计量都给计算出了。
第一个值是R^2,第二个值是F,第三个值是与F对应的概率p(p小于alpha则拒绝H0),第四个是残差的方差S^2.(S称作剩余标准差)
【判定标准:先看S^2要小,再看判定系数R^2是y估的变异占y的变异比重,接近于1;再看F和p,F要大于对应F分布的上α分位点,p要大于显著性阿尔法,则通过了回归形式的检验;有必要还要再看每一个参数的t检验,即拒接t检验H0,这里t参数要自己算(下面举例子)】
残差及其置信区间可以用rcoplot(r,rint)画图。
MATLAB中的多元二项式回归:
函数:rstool(x,y,model,alpha):
param:
x:是n*m的矩阵,每一行是一条数据,行数是样例数
y: n维向量
alpha:显著性水平
model:取下列值
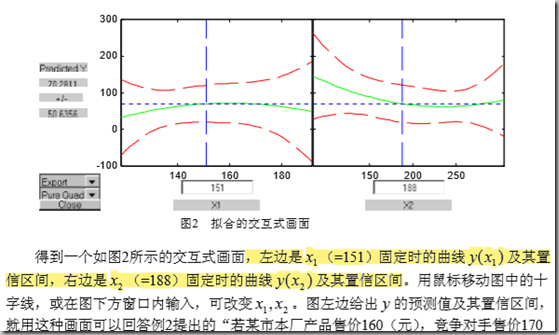
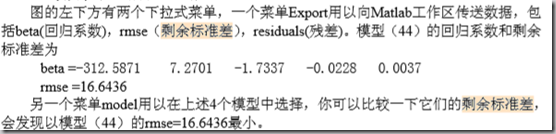
这个函数会得到拟合的交互式画面。会显示其他变量固定时,另一个变量的的置信区间。另外可以手动改变固定值。
并且,可以保存系数、残差向量、剩余标准差(残差的方差开根号)
MATLAB中的一元多项式回归:
就是拟合的ployfit命令
[p,s]=polyfit(x0,y0,n); p
param:
x0,y0即拟合的点
n:要拟合的多项式次数
return:
p:系数矩阵,按次数从高到低排列
s:数据结构,用来计算函数值以及置信区间
[y,delta] = polyconf(p,x0,s)
param:
p是系数矩阵
x0是要计算的点
s:polyfit的返回参数s
return:
y:拟合值
delta:置信区间半径
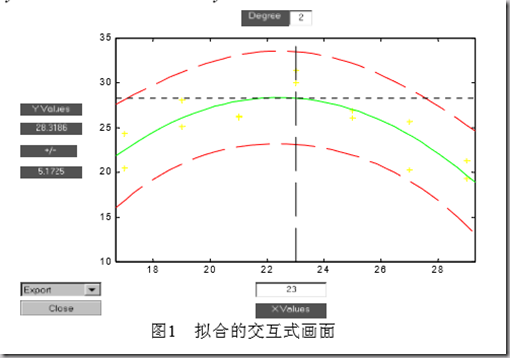
图形画面工具箱命令:polytool(x0,y0,n):
得到交互式画面,显示拟合曲线以及两条红线,表示置信上限和下限,如:
偏相关系数:又称作净相关系数,不考虑其他,只考虑一个xi与y的相关程度。(偏相关系数的检验)
->重点:变量筛选
变量筛选是建立简单回归分析模型所最常使用的方法,这个在简单回归模型中最重要,之后可以再采取高级的偏最小二乘回归分析等方法。
直接指定一个回归形式并使用所有变量进行多元回归,是过于武断的,这样的效果往往不好。
选择自变量时,一方面希望不遗漏重要的解释变量;另一方面希望参数尽量少,以降低模型复杂度。假设有m组数据,选定自变量数m。有效的方差有向前选择(逐渐增加变量)、向后选择(逐渐减少变量)和逐步回归法(结合上述)。
首先必须学习偏F检验的基本知识。
在决定一个新的变量是否有必要进入模型,或者判断某个变量是否可以从模型中删 除时,我们首先要问的问题是:这个变量能否对 y 提供显著的附加解释信息?回答这 个问题的方法是采用偏F 检验。
偏F检验规则:
为此进行△Rj方的假设检验:
检验统计量为:
式中, Qj 是减模型的残差平方和,Q为全模型的残差平方和。
Fj服从F分布。
决策为:
若拒绝H0,则引入该变量。否则不引入。
方法1:向前选择变量法
方法2:向后选择变量法
方法3:逐步回归
写作时需要说明为什么要用逐步回归:
边退边进的逐步回归方法:
调整复判定系数:
MATLAB逐步回归命令:
stepwise(x,y,inmodel,alpha):只能进行多元线性模型
param:
x,y:n*m和n*1,n条数据
inmodel:矩阵x列数的指标,给出初始模型中包括的子集(模型开始时已经选中的变量)。(缺省为空)
alpha:显著性水平
return:
逐步回归界面。在界面上进行一系列分析和工作。
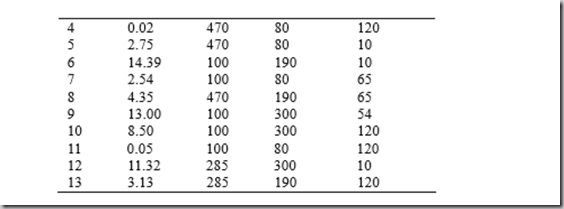
一个向前选择变量、向后选择变量分析的例子(注意函数的套用,以及分析的语言说明):
最后,在说一个非线性回归。
非线性回归并不是目标y对变量x的非线性,而是对回归系数而言的非线性。
Matlab统计工具箱中的nlinfit,nlparci,nlpredci,nlintool,不仅给出拟合的回归系数, 而且可以给出它的置信区间,及预测值和置信区间等。给一个例子,具体用到要查阅函数手册以及套用相关函数。
这些函数都是产生交互式界面,export可以传出相关指标如剩余标准差。
其他没有阅读的:
§7 复共线性与有偏估计方法前面我们详细讨论了回归系数的小二乘估计,并且证明了它的许多优良性质。 随着电子计算机技术的飞速发展,人们愈来愈多地有能力去处理含较多回归自变量的大 型回归问题。许多应用实践表明,在这些大型线性回归问题中,小二乘估计不是总令 人满意。例如,有时某些回归系数的估计值的绝对值差异较大,有时回归系数的估计值 的符号与问题的实际意义相违背等。研究结果表明,产生这些问题的原因之一是回归自 变量之间存在着近似线性关系,称为复共线性(Multicollinearity)。
§8 岭回归以及检验
用到查阅吧。









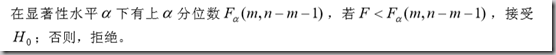
![image_thumb[2] image_thumb[2]](https://images2018.cnblogs.com/blog/1044022/201807/1044022-20180725113624924-30273370.png)
![image_thumb[1] image_thumb[1]](https://images2018.cnblogs.com/blog/1044022/201807/1044022-20180725113625818-569169018.png)