定义
Prufer序列用以解决一类树计数问题。
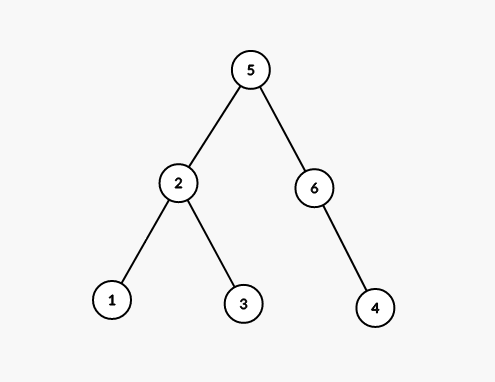
其的生成方式为:每次在所有叶子中选取编号最小的,将其的父亲编号推入序列,并删除这个叶节点,只到只剩两个
如上图这颗树的\(Prufer\)序列为\([2,2,6,5]\)。
考虑如何从\(Prufer\)序列反向生成树。
依次确定父亲。
首先选择未出现在序列中的编号最小未使用的节点,其父亲就是队首元素,将其退队。
若队首元素是最后一次出现,把其也加入未出现在序列的集合里。
有标号无根树的计数
考虑\(Prufer\)序列和原树一一对应,所以我们直接计序列计数即可,发现其为\(n^{n - 2}\)。
有标号有根树的计数
考虑对无根树确定根,其为\(n ^ {n - 2} * n = n^{n - 1}\)
若干强制条件如\(d_i = x\)的树计数
考虑对每个条件先确定其位置,再确定其他位置。
\(\prod_{i = 1} \binom{n - \sum_{j = 1}^{i - 1} {d_j - 1}}{d_i - 1} \times (n - \sum_{j = 1}d_j - 1) ^ {n - 2 - \sum_{j = 1}d_j - }\)