摘要
本文是面向开发者的进程代数基本入门级文章,很多技术人员对纯粹理论性的东西望而却步,但是对这些东西有所了解有助于大家的计算机理论思维,我希望尽量以最直观而简单的方式让大家快速充电,本文介绍进程代数的定义,历史,基本概念。由于作者水平有限,请读者在留言板提出修改意见!
阅读基础
读者应该拥有离散数学、计算理论和计算机软件和系统相关的知识基础!本文不适合理论研究专业人士阅读!
关键词: 进程代数,通信科学,并发理论,分布式理论
引言
计算机科学是个非常年轻的科学,非常多的研究至今可能都不超过50年,很多研究的都可以追溯到20世纪50年代,而那个时候从事计算机事业的大师们很多今天仍健在。所以相对而言,我们对与一些事情的历史可以更加细致地但不会过于冗长地进行介绍。通过本文,我希望读者了解到进程代数是什么,并可以在脑中形成一条简单的时间线,清楚地看到进程代数发生的历史。
什么是进程代数
首先声明一点,通过中文学习这些理论知识有的时候比较困难的一个主要原因是:翻译问题,上下文语义和语境环境,在中文中不成体系,所以我们阅读英文原文反而会得到更快速的理解和认识,而阅读中文教程反而是一头雾水,那是必须的。
进程代数英文为:process algebra,在英文中,这个词组中的process代表一个system(系统的)behavior(行为);一个系统就是一个能表现出各种行为的事物,在计算机世界,process主要指一个软件系统的行为;这句话很抽象,说白了就是,一个软件系统可以表现为一个动作(action),比如转换一个文件的格式,也可以发生一个个事件(event),比如格式转换完毕,另外,一个软件系统也可以在一定的序列下完成一系列动作(action);我们可以从各个角度(aspect)去观察一个系统的行为。研究者往往会关注一个角度的系统行为,这是他们会把系统进行抽象,称这种抽象为对系统行为的一种观察(observation)
有一些研究人员,以这样的一个角度观察系统的行为:
- 系统由一大堆动作(action)组成
- 动作之间都是离散的(discrete),独立的
- 离散的意思是action发生在某一时间,各个action发生的时间是独立的,不相关的
离散数学中,群(Group)是一个代数结构,它的运算符特性满足该群的约束要求,比如群(G,*)是一个代数系统,其中运算符*要满足结合律的要求,从群论的角度来看,进程代数是一个以进程为基本元素,并且进程上的运算符满足特定的约束的代数结构。
进程代数理论中提出了许多种模型,其中最早的(大约是20世纪中期)、最简单的模型是:将行为看做是一个带有输入/输出的函数,在进程开始时,给予一个输入值,在进程的执行过程中的某个时刻会给予外界它的某个输出值。这个模型是基于有穷自动机理论的,即每个process被看做一个自动机(automaton)【注:今天仍然有人将一个process看作自动机,进行研究】,一个自动机有很多状态(state)和迁移(transition),状态通过迁移进行状态之间之间的转换,这样,用自动机代表一个进程时,状态之间的迁移就代表进程执行了一个动作,所以迁移描述了进程的最基本行为,另外,一个自动机还可以有一个初始状态和多个终止状态。一次行为(behiour)就是一个自动机迁移的实例,即从初始态到达某一个终止态的具体路径过程。
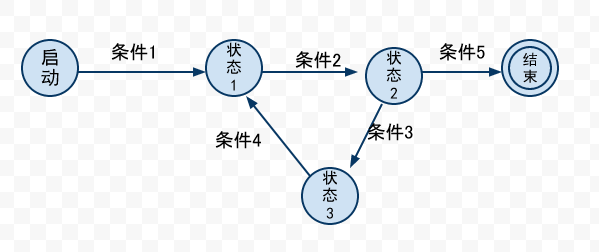
那么进程代数可以说是并行理论中的一个研究方向,所以我们在后面会看到,一种进程代数通常都会有一个基本的运算符——并行组合(parallel composition),这里组合(compostion)是指多个离散的动作的组合。除了并行的组合,还有带有选择分支的组合(alternative composition--choice)和按顺序组合(sequential composition--sequencing),这样,我们就可以对系统使用进程代数建模,然后通过代数的运算,方程推导进行分析和验证以判断系统是否满足我们所希望的特性。
进程代数的定义
我们使用加号“ +” 作为 alternative composition, 分号“;” 作为sequential composition,而双竖线“||” 表示 parallel composition.那么我们定义以下法则:
- – x + y = y + x (commutativity of alternative composition)
- – x + (y + z) = (x + y) + z (associativity of alternative composition)
- – x + x = x (idempotency of alternative composition)
- – (x + y); z = x; z + y; z (right distributivity of + over ;)
- – (x; y); z = x; (y; z) (associativity of sequential composition)
- – x k y = y k x (commutativity of parallel composition)
- – (x k y) k z = x k (y k z) (associativity of parallel composition)
如果任何带有三个运算符的代数结构满足以上七条法则,那么就称这个代数为进程代数,这就是一个简单的进程代数的概念定义。
文献[2]中这样说道:
历史
谈到进程代数,很多人会想到Petri-net,在进程代数之前,这个1962年由Petri发明的形式化方法是并行理论的唯一工具,用来研究并行和分布式系统。
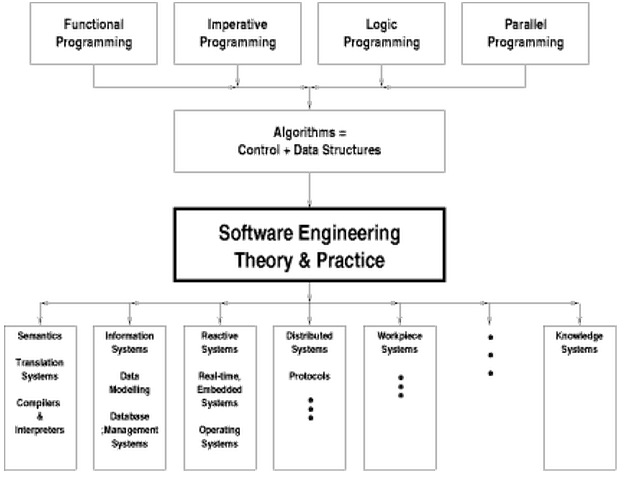
1970年的时候,世界上关于计算(computation)的形式化推理方法,基本分为三种:
- 操作语义学(Operational semantics)——通过语言的实现方式定义语言的语义,也就是将语言成分所对应的计算机的操作作为语言成分的语义。因为语言的语义应该是标准的,不应依赖于特定的计算机系统,或一种具体的实现方式,因此,操作语义学使用抽象机和抽象解释程序来定义语言的语义。
- 指称语义学(Denotational semantics)——通过执行语言成分所要得到的最终效果来定义该语言成分的语义。指称语义学方法认为语言成分的含义是语言成分本身固有的,不依赖于具体实现该语言成分的计算机。对同一种语言成分,不同的计算机的执行实现过程可以不同,但所产生的最终效果应该是相同的。这种最终效果被看作是语言成分所指称的外在物体,称作语言成分的指称物。指称物多为数学对象,如整数、集合、函数等。指称语义学方法在定义语言的语义时,先确定指称物,然后给出语言成分到指称物的语义映射,这种映射必须满足两个条件:每个语言成分都对应有指称;复合成分的指称只依赖于它的子成分的指称。论域理论是指称语义学方法的数学基础。
- 公理化语义(Axiomatic semantics)——通过使用数学中的公理化方法,用公理系统定义程序设计语言的语义。另外,公理语义学还研究和寻求适用于描述程序语义、便于语义推导的逻辑语言。例如,用时态逻辑定义的语言的公理语义又称为时态语义。典型的公理语义方法是Hoare公理系统。
但是上面三种方法并不能给出带有并行运算符的程序的语义,即不能通过形式化方法进行建模,也无法进行推理、验证等工作,为了解决这个问题进程代数应运而生,下面我们介绍三个重要的进程代数方法。
Bekič
奥地利维也纳的IBM实验室在整个60年代和70年代都以其程序语言的定义和语义方面的研究而著称,这个期间Hans Bekič就工作在这里,他主要从事ALGOL和PL/I(相信学过计算机的同志对这些名词都有点眼熟)的指称语义方面的研究,但是针对PL/I的parallel composition运算符如何指定指称语义遇到了困难,他提出了一个类并行组合运算符(quasi-parallel composition operator),后来更正为并行组合运算符,并提出了一些其他的基本运算和概念,使得进程代数的一些基本概念开始浮现,但是还不成熟,下图是相关论文中出现的运算示例:
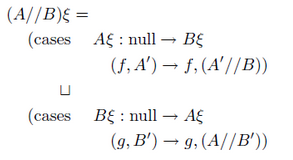
CCS
进程代数历史上最重要的人物是Robin Milner,1973至1980年间发明了CCS(Calculus of Communicating Systems,通信系统演算),是用于描述通信并发系统的代数理论。
假定一个标号集L,其补集Act=L∪L∪{τ}称为动作集,其中τ是特殊的不可见动作。CCS的进程构造算子如下: 算子 直观意义 0 空进程 a.P 动作前缀(a∈Act) P+Q 非确定选择 P|Q 并行复合 P\S 限制(S L) P[f) 换标号(f是从L到L的部分函数)此外还允许递归算子。 CCS的语义由结构化操作语义方法给出,下面列出几条典型的语义规则。P→Q表示进程P可执行动作a而演变为Q。 从关于并行算子|的规则可以看出,由两个进程并行复合而成的进程可以做每个分进程所能做的动作(PAR1)和(PAR2),但当两个分进程同时执行一对互补的动作时,则发生通信,产生τ动作(COM)。这种通信方式称为握手式通信。CCS的基本思想是用τ和+来模拟|,将并发归结为非确定性,即所谓交错语义。这一思想体现在下面的展开律中: CCS采用互模拟作为基本的进程等价关系。强互模拟等价满足下面的Monoid公理: P+0=P,P+P=P,P+Q=Q+P, (P+Q)+R=P+(Q+R) 对观察等价(将τ忽略不计)还成立三条,—公理: a.τ.P=a.P, P+τ.P=τ.P, a.(P+τ.Q)+a.Q=a.(P+τ.Q) 上面介绍的CCS称为基本CCS,或纯CCS,进程之间只能通过执行互补动作实现同步,而不能直接进行通信。全CCS引入输出动作c<-e和输入动作c->x, c<-e表示沿通道c发送数据表达式e的值,c->x表示从通道c接收一个值赋给x,此外还有条件表达式if- then-else。用全CCS可以直接描述进程间的通信。
CSP
Tony Hoare是另一位重要的人物。关于CSP的详细可以在此下载到:http://www.usingcsp.com/cspbook.pdf,1978年C. A.R.Hoare提出的通信顺序进程 CSP,是面向分布式系统的程序设计语言。在该语言中,一个并发系统由若干并行运行的顺序进程组成,每个进程不能对其他进程的变量赋值。进程之间只能通过一对通信原语实现协作:Q->x表示从进程Q输入一个值到变量x中;P<-e表示把表达式e的值发送给进程P。当P进程执行Q->x,同时Q进程执行P<-e时,发生通信,e的值从Q进程传送给P进程的变量x。后来出现的实用编程语言OCCAM即以CSP为基础发展而成。 1984年S.Brooks,C.A.R.Hoare和W.Roscoe提出CSP理论(TCSP)。这是一个代数演算系统,其基本成分是事件(或动作)。进程由事件和一组算子构造而成。典型的算子有:→(前缀),|(外部非确定性选择), (内部非确定性选择) (交错并行), (同步并行),\e(事件隐蔽),以及递归等。 例:(自动售货机) VM=coin→(choc→VM|coffee→VM), CUST:coin→(choc→CUST coffee→CUST) 这里定义了两个进程:VM(售货机)和CUST (顾客)。售货机在接受了硬币coin后,可按顾客的要求支付choc或coffee。顾客在付了硬币后,或者想要choc,或者想要coffee,其选择不受外界影响。 与CCS不同(也与作为程序设计语言的CSP不同),TCSP采用的是广播式通信,而不是握手式通信,即只有当并行运行的各进程都执行同一动作时,才发生同步。 TCSP采用失败等价作为确定进程等价的准则,这也称为失败语义。一个失败是一二元组(s,X),其中s是事件的有限序列,X是事件集(称为拒绝集)。若进程P可以执行事件序列s,且到达一个无法执行X中任一事件的状态,则称(s,X)是P的一个失败。例如,设有进程P=a→(b→c→STOP|b→d→STOP),则(ab,{c})是P的一个失败,因为P可执行ab,变成d→STOP而无法做c。类似地,(ab, {d})也是P的一个失败,但(ab,{c})不是。两个进程失败等价当且仅当它们具有相同的失败集。例如对自动售货机的例子,可以证明进程VM|CUST与CUST失败等价。 利用失败可以构造TCSP的指称模型,在此模型中,失败等价的进程被解释为同一个元素。关于失败等价建立了一些公理系统,可以对语义上的等价关系进行形式推导。
结语
关于进程代数更详细的知识,读者可以参考文献,或搜索相关英文关键词可以看到大量的英文资料,中文资料目前较少,不得不赞国外在知识分享方面的优秀之处。
参考文献
- [1]http://theory.stanford.edu/~rvg/process.html
- [2]http://www.spatial.maine.edu/~worboys/processes/baeten%20history%20PA.pdf
- [3]http://www.suanshu.net/list/2009/05/09/13687.htm
- [4]http://qzone.qq.com/blog/55959211-1220073445
- [5]http://old.blog.edu.cn/user1/2746/archives/2007/1628822.shtml
- [6]北大SEForge上的WIKI