You have unweighted tree of nn vertices. You have to assign a positive weight to each edge so that the following condition would hold:
- For every two different leaves v1v1 and v2v2 of this tree, bitwise XOR of weights of all edges on the simple path between v1v1 and v2v2 has to be equal to 00.
Note that you can put very large positive integers (like 10(1010)10(1010)).
It's guaranteed that such assignment always exists under given constraints. Now let's define ff as the number of distinct weights in assignment.
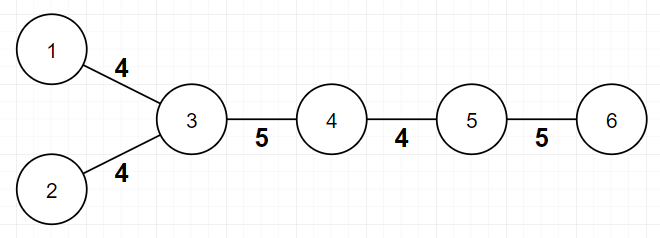 In this example, assignment is valid, because bitwise XOR of all edge weights between every pair of leaves is 00. ff value is 22 here, because there are 22 distinct edge weights(44 and 55).
In this example, assignment is valid, because bitwise XOR of all edge weights between every pair of leaves is 00. ff value is 22 here, because there are 22 distinct edge weights(44 and 55).
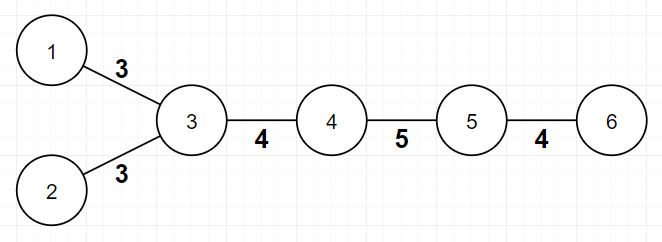 In this example, assignment is invalid, because bitwise XOR of all edge weights between vertex 11 and vertex 66 (3,4,5,43,4,5,4) is not 00.
In this example, assignment is invalid, because bitwise XOR of all edge weights between vertex 11 and vertex 66 (3,4,5,43,4,5,4) is not 00.
What are the minimum and the maximum possible values of ff for the given tree? Find and print both.
The first line contains integer nn (3≤n≤1053≤n≤105) — the number of vertices in given tree.
The ii-th of the next n−1n−1 lines contains two integers aiai and bibi (1≤ai<bi≤n1≤ai<bi≤n) — it means there is an edge between aiai and bibi. It is guaranteed that given graph forms tree of nn vertices.
Print two integers — the minimum and maximum possible value of ff can be made from valid assignment of given tree. Note that it's always possible to make an assignment under given constraints.
6 1 3 2 3 3 4 4 5 5 6
1 4
6 1 3 2 3 3 4 4 5 4 6
3 3
7 1 2 2 7 3 4 4 7 5 6 6 7
1 6
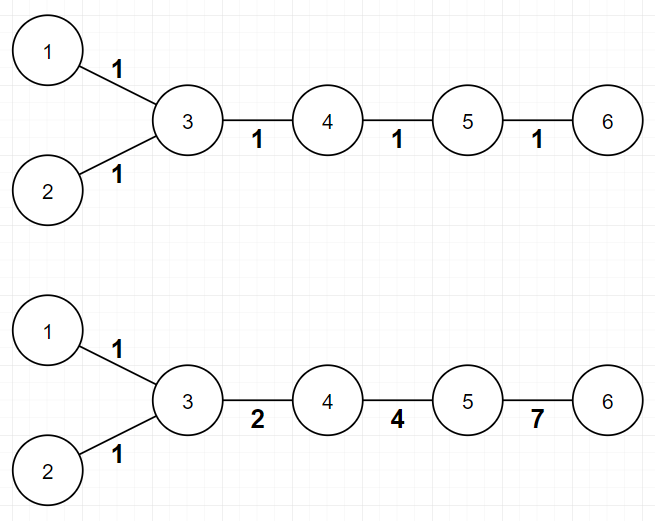
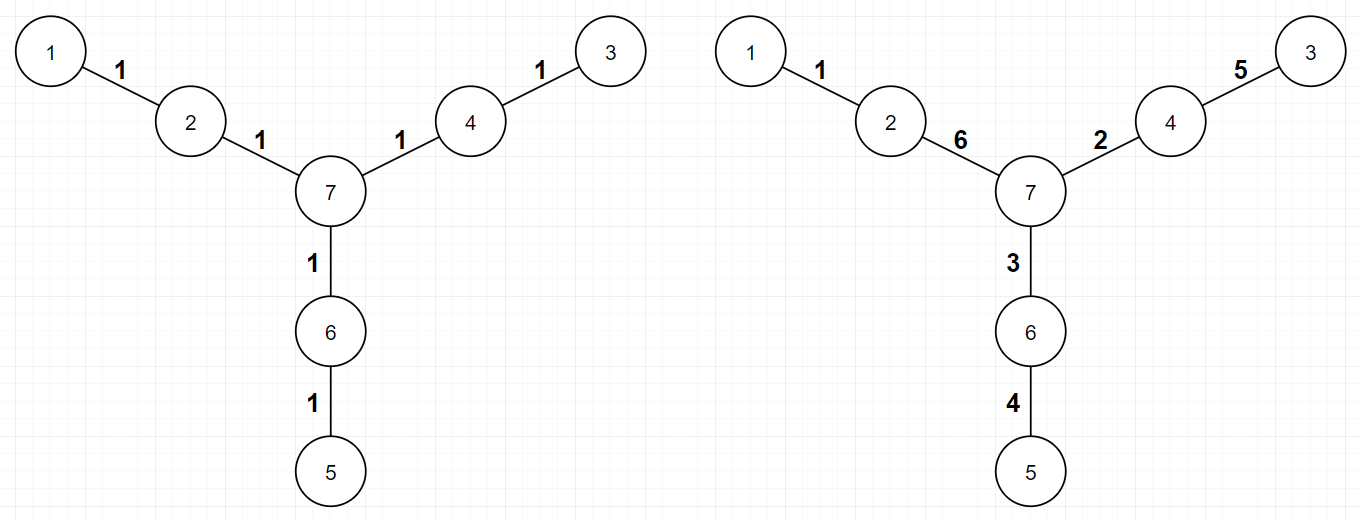
In the first example, possible assignments for each minimum and maximum are described in picture below. Of course, there are multiple possible assignments for each minimum and maximum.
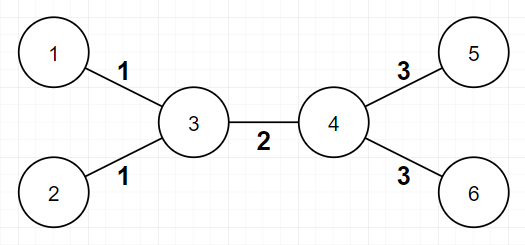
In the second example, possible assignments for each minimum and maximum are described in picture below. The ff value of valid assignment of this tree is always 33.
In the third example, possible assignments for each minimum and maximum are described in picture below. Of course, there are multiple possible assignments for each minimum and maximum.
#include <iostream> #include <vector> #include <algorithm> #include <string> #include <set> #include <queue> #include <map> #include <sstream> #include <cstdio> #include <cstring> #include <numeric> #include <cmath> #include <iomanip> #include <deque> #include <bitset> //#include <unordered_set> //#include <unordered_map> #define ll long long #define pii pair<int, int> #define rep(i,a,b) for(int i=a;i<=b;i++) #define dec(i,a,b) for(int i=a;i>=b;i--) #define forn(i, n) for(int i = 0; i < int(n); i++) using namespace std; int dir[4][2] = { { 1,0 },{ 0,1 } ,{ 0,-1 },{ -1,0 } }; const long long INF = 0x7f7f7f7f7f7f7f7f; const int inf = 0x3f3f3f3f; const double pi = 3.14159265358979323846; const double eps = 1e-6; const int mod = 1e9 + 7; const int N = 1e5 + 5; //if(x<0 || x>=r || y<0 || y>=c) inline ll read() { ll x = 0; bool f = true; char c = getchar(); while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); } while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar(); return f ? x : -x; } ll gcd(ll m, ll n) { return n == 0 ? m : gcd(n, m % n); } ll lcm(ll m, ll n) { return m * n / gcd(m, n); } bool prime(int x) { if (x < 2) return false; for (int i = 2; i * i <= x; ++i) { if (x % i == 0) return false; } return true; } ll qpow(ll m, ll k, ll mod) { ll res = 1, t = m; while (k) { if (k & 1) res = res * t % mod; t = t * t % mod; k >>= 1; } return res; } vector<vector<int>> g(N); int d[N],fg,res1=0; void dfs(int u,int fa, int dep) { d[u] = dep; if (g[u].size() == 1 && (d[u] & 1)) fg = 1; for (auto v : g[u]) { if (v == fa) continue; dfs(v, u, dep + 1); } } int main() { int n; cin >> n; rep(i, 1, n - 1) { int u, v; cin >> u >> v; g[u].push_back(v); g[v].push_back(u); } int root; rep(i, 1, n) { if (g[i].size() == 1) { root = i; break; } } dfs(root, -1, 0); int minn = fg ? 3 : 1; int maxn = n - 1; rep(u, 1, n) { int cnt = 0; for (auto v : g[u]) if (g[v].size() == 1) cnt++; maxn -= max(0, cnt - 1); } cout << minn <<" "<< maxn << endl; return 0; }