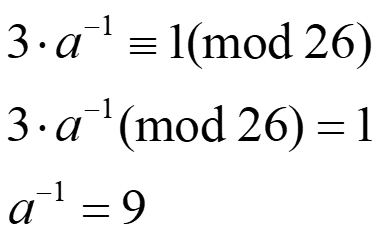数论倒数,又称逆元
取模
对于取模,有一下一些性质:
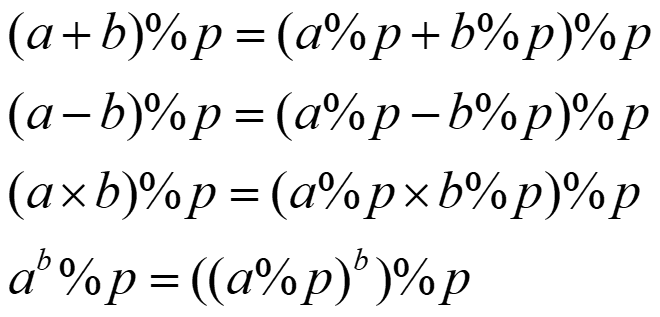
但是唯独除法是不满足的:
![]()
为什么除法错的呢?很好证明:
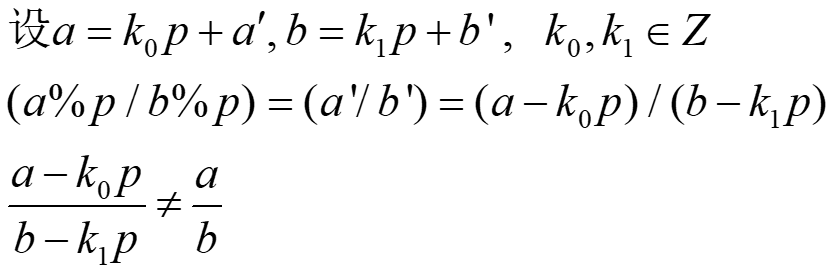
而对于一些题目,我们必须在中间过程中进行求余,否则数字太大,电脑存不下,那如果这个算式中出现除法,我们就需要逆元了。
逆元
定义:

我们知道,如果a*x = 1,那么x是a的倒数,x = 1/a
而在数论问题中,大部分情况都有取模,所以问题就变成了:
![]()
这时x在数值上就不一定等于我们常规意义上的1/a了,我们可以理解为要求在0,1,2……p-1之间找一个数,是的这个数和a相乘后再取模p,得到的结果为1。
现在就要在回到刚才的问题了,除以一个数等于乘上这个数的倒数,在除法取余的情况下,就是乘上这个数的逆元,即:
![]()
这样就把除法,完全转换为乘法了。
逆元的求解
对于逆元的求解,如果n较小的话,是容易算出来的,例如,求3在模26下的逆元:
但是当n非常大的时候,就需要引入一个算法来计算
(1)扩展欧几里得算法(extend_gcd)
![]()
对于逆元的表达式可以做一些变换:
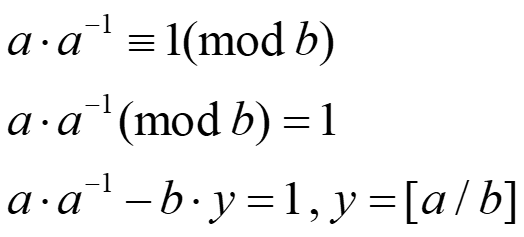
当gcd(a,n)=1时,代入extend_gcd(a,n,x,y),得到的非负的x值,就是a对模n的逆元。
算法实现与证明
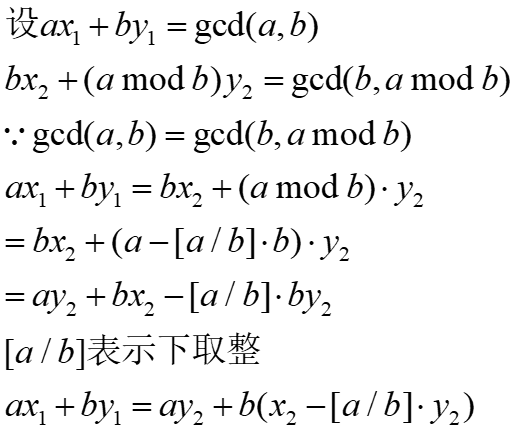
也就是说,我们得到了一个和gcd算法中,gcd(m,n)=gcd(n,m%n)相似的恒等式
![]()
什么意思呢?举个例子,就是

如果想要x为正值,根据
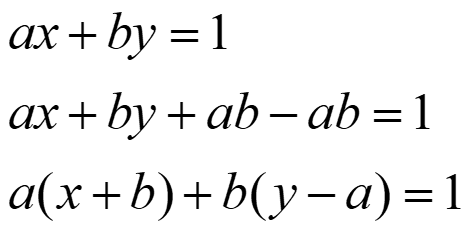
只再做一步:
if (x < 0) { x += b; y -= a; }
扩展:

完整算法:
int extend_gcd(int a, int b, int& x, int& y) { if (b == 0) { x = 1, y = 0; return a; } int q = extend_gcd(b, a % b, x, y); int temp = x; x = y; y = temp - a / b * y; return q; }
(2)费马小定理
如果p是一个质数,并且gcd(a,p)=1
![]()
两边同除以 a
![]()
所以
![]()
用快速幂求一下,复杂度O(logn)
(3)不知道叫啥
当p为质数时有![]()
证明:
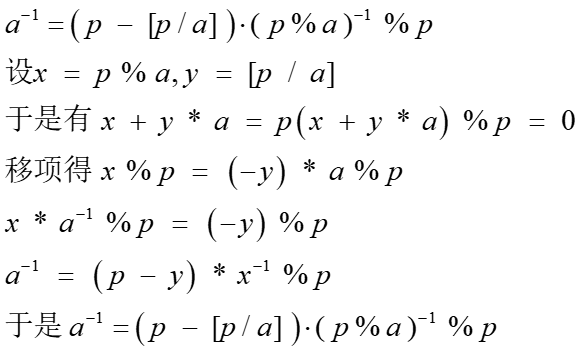
写成算法就是一个递归,到1为止,因为1的逆元就是1
int inv(int t, int p) { return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p; }
这个方法复杂度是O(n),但并不是说比前两个差,它可以在O(n)的复杂度内算出n个数的逆元,上面的算法加一个记忆性搜索就行了
int inv(int t, int p) { return INV[t] = t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p; }