目录:
- Dictionary Data Structure 词典数据结构
- Wild-Card Query 通配符查询
- Spelling Correction 拼写纠正
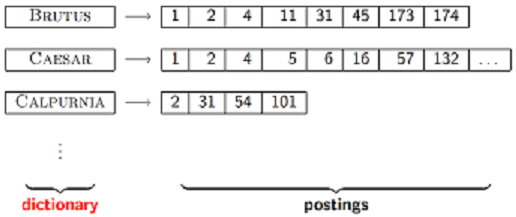
- 索引词(term vocabulary)。
- 文档频率(document frequency,即这个词在多少个文档里出现)。
- 指向倒排表的指针(pointers to each postings list )。


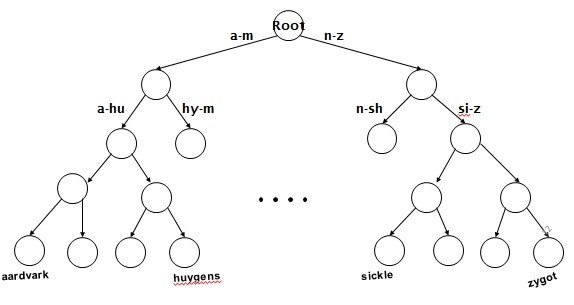
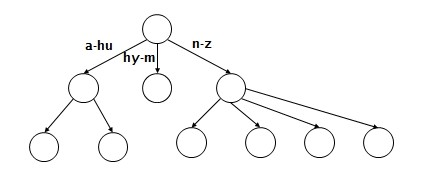
一棵m 阶的B-树满足下列特性的m 叉树:
- 树中每个结点至多有m 棵子树;
- 若根结点不是叶子结点,则至少有两棵子树;
- 除根结点之外的所有非终端结点至少有[m/2] 棵子树;
- 所有的非终端结点中包含以下信息数据:(n,A0,K1,A1,K2,…,Kn,An)。其中:Ki(i=1,2,…,n)为关键码,且Ki<Ki+1,Ai 为指向子树根结点的指针(i=0,1,…,n),且指针Ai-1 所指子树中所有结点的关键码均小于Ki (i=1,2,…,n),An 所指子树中所有结点的关键码均大于Kn。n为关键码的个数。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
这样讲起来或许比较枯燥难懂,看这张图就好了:
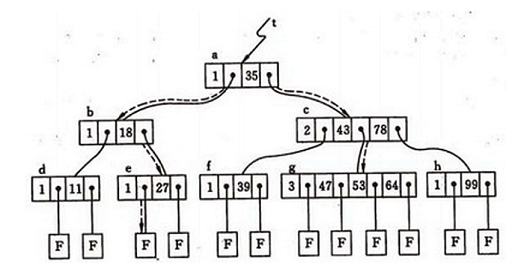
树的优点就是可以解决前缀查找的问题了。
缺点是速度比哈希慢点,是O(logM)并且要求是平衡的,重新平衡一棵树的代价大。(虽然B-树减轻了这种代价)
Wildcard queries,通配符查询。
比如查询语句 mon*:找出所有以mon开头的单词。如果采用树(或者B-树)结构词典,我们可以很容易的解决,只需要查询范围在mon ≤ w < moo的所有单词就ok了。
但是查询语句 *mon:找出所有以mon结尾的单词就比较困难了。其中一种办法就是我们增加一个额外的B-树来存储所有单词,以从后向前的顺序,然后在这个树上查询范围在nom ≤ w < non的所有单词。
可是如何处理通配符在单词中间的查询呢?
比如query是co*tion的话。我们当然可以分别在B-树查询到co*和*tion的所有单词然后合并这些单词,但是这样开销太大了。
解决办法就是:轮排索引(Permuterm Index),我们把query的通配符转换到结尾处。
设置一个标志$表示单词的结尾。
以hello举例,hello可以被转换成hello$, ello$h, llo$he, lo$hel, o$hell。$代表中hello的结束。现在,查询X等于查询X$,查询X*等于查询X*$,查询*X等于查询X$*,查询X*Y等于查询Y$X*。对于hel*o来说,X等于hel,Y等于o。
既然我们已经把通配符都弄到了单词尾部,现在我们又可以通过B-树像以前那样查询拉。
以上,我们已经完成了对query的转换,那么那些存储的索引的词要怎么处理才能配合这种query查询呢?
我们对索引来建立索引!!
Bigram indexes。就是两两个字母来索引。
举例来说,一个文本是“April is the cruelest month”,分别成Bigram indexes就是“$a,ap,pr,ri,il,l$,$i,is,s$,$t,th,he,e$,$c,cr,ru,ue,el,le,es,st,t$, $m,mo,on,nt,h$”,其中$ 代表着单词边界的符号。
那么如何对索引建立索引??
维护第二个倒排表,倒排表的索引词是Bigram indexes,posting list的值就是与之匹配的dictionary terms。
像这样:
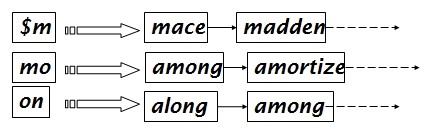
好了!目前为止,我们既对query进行了处理,也对terms进行了处理。
所以现在如果我们要查询 mon*,query会被分解成 $m AND mo AND on ,然后从上图中的倒排表做两个AND可以得到匹配的terms了!!
但是,我们会发现 $m AND mo AND on 也会匹配到单词moon,而moon不符合mon*的格式,这是他的一个缺点。我们必须要过滤掉这些词。
另外,一条查询语句往往相当多的布尔查询,这个开销也挺大的。
Spelling correction,拼写校正。
我们google一下 Alanis Morisett ,得到结果如图:
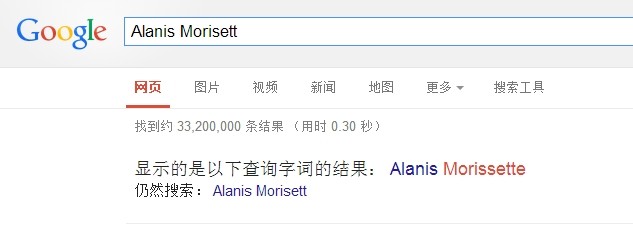
对了,就是这个提示,您找的是不是:xxxxxx。
在搜索引擎中,需要有一个可以查询到所有正确单词的词典。
给定一个词典和一个query,返回一个和query最接近的words。
怎么用才算是最接近??
- 编辑距离算法。
- 带权编辑距离算法。
编辑距离(Edit distance):
给定两个字符串S1和S2,从S1转换到S2的最小步骤就是他们的编辑距离。这些步骤包括,Insert(1步), Delete(1步), Replace(1步),copy(0步)。
比如说:
dof到dog的编辑距离是1,cat到act的编辑距离是2,cat到dog的编辑距离是3.
算法导论里关于编辑距离的伪代码如下:

举例子:算cats到fast的编辑距离~
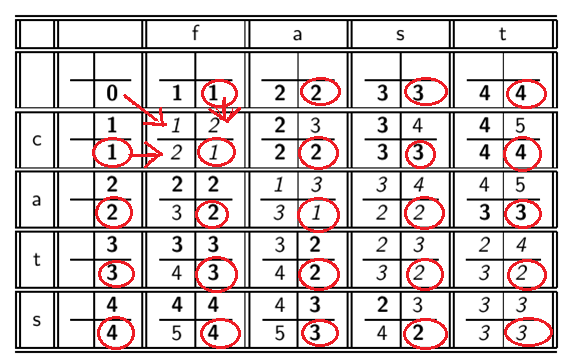
括号里圈出来的表示实际应该填的值,其他的只是用来进行对比,取其中最小的数。
具体到表中的每一格中四个数字的含义就是:

从左边的格子过来代表增加,上边的格子过来代表删除,斜上角的格子过来代表替换(此时两个字符不相等)或复制(此时两个字符不相等)。
编辑距离就是这样子。那么什么是带权编辑距离呢?
比如说,我们打字的时候,m被错打成n的几率会比m错打成p的几率更大,所以我们应该认为m和n的编辑距离小于m到p的编辑距离。因此将m替换为n时计算编辑距离应该比将m替换为p时的编辑距离小。
实现带权编辑距离,我们需要一个额外的权值矩阵。
那么,给定一个查询词,我们是不是得计算这个查询词和所有的索引词之间编辑距离呢?
答案是否定的,因为这样开销很大而且慢。
怎么用减少计算呢??
比如说,如果query是lord:
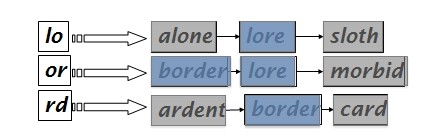
我们只取lo,or,rd中有重叠两次或以上的term,然后合并这些term,以这个为范围进行编辑距离的计算。
索引
其实在计算机中我们早已接触过跟索引有关的东西,比如数据库里的索引(index),还有硬盘文件系统中其实也有类似的东西,简而言之,索引是一种为了方便找到自己需要的东西而设计出来的条目,你可以通过找索引找到自己想要内容的位置。索引过程是: 关键字->索引->文档。在图书馆内的书分门别类,就是一种按类别来分的索引。当然索引还有很多其他的实现。
仅仅有索引的概念是不够的。虽然分门别类是一种方法,但是我们在拥有一堆文档的时候必须要有从文档到索引的规范过程,并且索引的结构要满足能够让人(或者计算机)快速找到的方法。面对一条长长的没有处理的索引列表,甚至还没有排好序,你可能要用O(N)的时间去看,头都大了。
为了满足这个要求,B+树,哈希表可以是比较好的选择,它们的复杂度分别是O(log N) 和 O(1)。
但是事实上为了满足特殊的要求,有些时候还要设计更加特殊的数据结构,比如后缀树组和trie树用来处理非文本的序列子串搜索。
在主要的搜索引擎中,还是靠文本搜索,而索引的设计其实并不固定,还要跟搜索策略结合,这些都是搜索引擎的部分。
倒排索引
倒排索引是索引的子集。在搜索引擎之中,正排索引跟倒排索引其实都有应用。
正排索引:知道文档d,得到d的关键字的位置序列,实现方式是 文档编号+关键字数组
倒排索引:知道关键字w,找到包含关键字的文档d1,d2,d3.... 实现方式是:关键字key做键的字典,值是文档编号数组
无论是哪一种索引,都要用一种能够快速检索的数据结构的来实现,否则它们都会面临大规模甚至超大规模的数据下无法工作的问题。
哈希表
哈希表,根据键找到值,复杂度为O(1)。它的实现是一组桶,每个桶=头部键+尾部链表。数据结构课程中对哈希表已经讲得很清楚了。它的问题在于空间消耗太大,而且可能会有哈希分配不平衡的问题。
跳表
参考一下 https://juejin.im/post/587c6cec61ff4b006501e006
跳表是一种特殊的链表,又称跳跃表,可以达到O(log N)的查询速度。这里的图说明了跳表的元素其实都在底层,但是可以有一些重复的层级为了方便检索。它的问题在于怎样平衡空间和时间效率上。
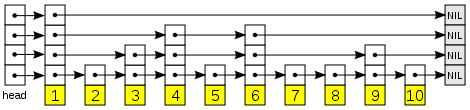
跳表中用到了概率,它设定某个跳表元素的i副本出现在i+1层的概率为p,根据概率对每个值求和得到元素k的期望出现次数 (∑p^k=1/(1-p), k = 1,2,...)。现实中并不会完全按照概率来进行设计,而是用一个固定的步长来设计多级的并联链表。
结论
倒排索引和跳表是为了方便检索和加快速度而设计的结构,并且在搜索引擎中为后续的其他操作提供了基础。现实中经常讲到的是倒排索引,以及跟它关联的tfidf。为了实现数据的快速搜索,还需要跟具体的数据结构相结合。
转载自:http://www.cnblogs.com/4everlove/p/3678414.html