回溯法之n皇后问题

1.问题描述

以八皇后为例进行问题描述：

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

---

图解回溯法解八皇后问题：

下面用N皇后问题来具体解释：

N皇后问题

从空棋盘开始，把皇后1放在第一行第一列。然后放皇后2，1、2列尝试失败，把它放在第三个位置，即格子(2,3)，但是这被证明是一个死胡同，因为皇后三将无位置可以放，因此皇后2回溯到(2,4)，这样皇后3可以放到(3,2)，但是这又是另一个死胡同。就这样不断的向下试探，不行就回溯到上层，直到找到最终的完整解。以下给出4皇后的状态空间树：

由以上分析不难得出若两个皇后位置分别是（i,j）和（k,l），且i-j=k-l或i+k=j+l,则说明这两个皇后处于同一斜线上。以上2个方程分别等价于i-k=j-l和i-k=l-j.由此可知只要｜i-k|=| j-l|成立，就表明2个皇后位于同一斜线上。

2.算法设计

1、使用一个一维数组表示皇后的位置，
   其中数组的下标表示皇后所在的行，
   数组元素的值表示皇后所在的列。

2、假设前n-1行的皇后已经按照规则排列好，
   那么可以使用回溯法逐个试出第n行皇后的合法位置，
   所有皇后的初始位置都是第0列，
   那么逐个尝试就是从0试到N-1，
   如果达到N，仍未找到合法位置，
   那么就置当前行的皇后的位置为初始位置0，
   然后回退一行，且该行的皇后的位置加1，继续尝试，
   如果目前处于第0行，还要再回退，说明此问题已再无解。

3、如果当前行的皇后的位置还是在0到N-1的合法范围内，
   那么首先要判断该行的皇后是否与前几行的皇后互相冲突，
   如果冲突，该行的皇后的位置加1，继续尝试，
   如果不冲突，判断下一行的皇后，
   如果已经是最后一行，说明已经找到一个解，输出这个解，
   然后最后一行的皇后的位置加1，继续尝试下一个解。

3.代码实现

#include <stdio.h>
int Queenes[8]={0},Counts=0;
int Check(int line,int list){
    //遍历该行之前的所有行
    for (int index=0; index<line; index++) {
        //挨个取出前面行中皇后所在位置的列坐标
        int data=Queenes[index];
        //如果在同一列，该位置不能放
        if (list==data) {
            return 0;
        }
        //如果当前位置的斜上方有皇后，在一条斜线上，也不行
        if ((index+data)==(line+list)) {
            return 0;
        }
        //如果当前位置的斜下方有皇后，在一条斜线上，也不行
        if ((index-data)==(line-list)) {
            return 0;
        }
    }
    //如果以上情况都不是，当前位置就可以放皇后
    return 1;
}
//输出语句
void print()
{
    for (int line = 0; line < 8; line++)
    {
        int list;
        for (list = 0; list < Queenes[line]; list++)
            printf("0");
        printf("#");
        for (list = Queenes[line] + 1; list < 8; list++){
            printf("0");
        }
        printf("
");
    }
    printf("================
");
}
void eight_queen(int line){
    //在数组中为0-7列
    for (int list=0; list<8; list++) {
        //对于固定的行列，检查是否和之前的皇后位置冲突
        if (Check(line, list)) {
            //不冲突，以行为下标的数组位置记录列数
            Queenes[line]=list;
            //如果最后一样也不冲突，证明为一个正确的摆法
            if (line==7) {
                //统计摆法的Counts加1
                Counts++;
                //输出这个摆法
                print();
                //每次成功，都要将数组重归为0
                Queenes[line]=0;
                return;
            }
            //继续判断下一样皇后的摆法，递归
            eight_queen(line+1);
            //不管成功失败，该位置都要重新归0，以便重复使用。
            Queenes[line]=0;
        }
    }
}
int main() {
    //调用回溯函数，参数0表示从棋盘的第一行开始判断
    eight_queen(0);
    printf("摆放的方式有%d种",Counts);
    return 0;
}

4.实现结果

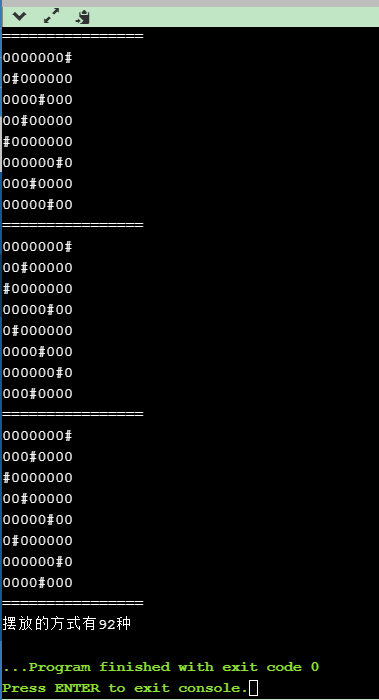
 参考：王晓东《算法设计与分析》第二版

            https://blog.csdn.net/sinat_33052719/article/details/51447531

            https://blog.csdn.net/yuer_xiao/article/details/82714734?depth_1-