导包
1 import numpy as np 2 import h5py 3 import matplotlib.pyplot as plt 4 5 plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots 6 plt.rcParams['image.interpolation'] = 'nearest' 7 plt.rcParams['image.cmap'] = 'gray' 8 9 np.random.seed(1)
Padding

函数解释:np.pad(array, pad_width, mode, **kwargs)
- array——表示需要填充的数组;
- pad_width——表示每个轴(axis)边缘需要填充的数值数目;
- 参数输入方式为:((before_1, after_1), … (before_N, after_N)),其中(before_1, after_1)表示第1轴两边缘分别填充before_1个和after_1个数值。取值为:{sequence, array_like, int}
- mode——表示填充的方式(取值:str字符串或用户提供的函数),总共有11种填充模式;
1 def zero_pad(X, pad): 2 """ 3 Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 4 as illustrated in Figure 1. 5 6 Argument: 7 X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images 8 pad -- integer, amount of padding around each image on vertical and horizontal dimensions 9 10 Returns: 11 X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C) 12 """ 13 14 ### START CODE HERE ### (≈ 1 line) 15 X_pad=np.pad(X,( 16 (0,0), #样本数,不填充 17 (pad,pad), #图像高度,你可以视为上面填充x个,下面填充y个(x,y) 18 (pad,pad), #图像宽度,你可以视为左边填充x个,右边填充y个(x,y) 19 (0,0)), #通道数,不填充 20 'constant', constant_values=0) #连续一样的值填充 21 ### END CODE HERE ### 22 23 return X_pad
单步卷积

图中蓝色方框与滤波器进行作用,计算获得值-5的过程就是一次单步卷积。
1 def conv_single_step(a_slice_prev, W, b): 2 """ 3 Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 4 of the previous layer. 5 6 Arguments: 7 a_slice_prev -- slice of input data of shape (f, f, n_C_prev) 8 W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev) 9 b -- Bias parameters contained in a window - matrix of shape (1, 1, 1) 10 11 Returns: 12 Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data 13 """ 14 15 ### START CODE HERE ### (≈ 2 lines of code) 16 # Element-wise product between a_slice and W. Do not add the bias yet. 17 s = np.multiply(a_slice_prev,W) 18 # Sum over all entries of the volume s. 19 Z=np.sum(s) 20 # Add bias b to Z. Cast b to a float() so that Z results in a scalar value. 21 Z=Z+float(b) 22 ### END CODE HERE ### 23 24 return Z
卷积神经网络-前向传播
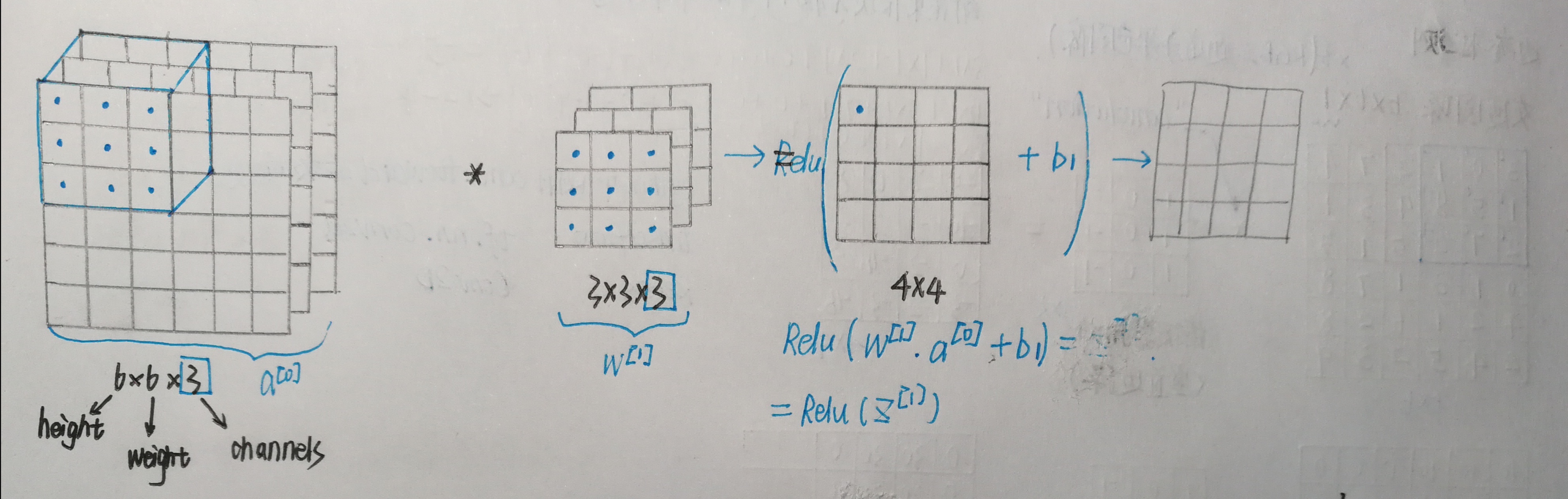

A_prev(shape = (5,5,3))的左上角选择一个2x2的矩阵进行切片操作:a_slice_prev = a_prev[0:2,0:2,:]
1 def conv_forward(A_prev, W, b, hparameters): 2 """ 3 Implements the forward propagation for a convolution function 4 5 Arguments: 6 A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) 7 W -- Weights, numpy array of shape (f, f, n_C_prev, n_C) 8 b -- Biases, numpy array of shape (1, 1, 1, n_C) 9 hparameters -- python dictionary containing "stride" and "pad" 10 11 Returns: 12 Z -- conv output, numpy array of shape (m, n_H, n_W, n_C) 13 cache -- cache of values needed for the conv_backward() function 14 """ 15 ### START CODE HERE ### 16 # Retrieve dimensions from A_prev's shape (≈1 line) 17 (m, n_H_prev, n_W_prev, n_C_prev)=A_prev.shape 18 # Retrieve dimensions from W's shape (≈1 line) 19 (f, f, n_C_prev, n_C)=W.shape 20 # Retrieve information from "hparameters" (≈2 lines) 21 stride=hparameters['stride'] 22 pad=hparameters['pad'] 23 24 # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines) 25 n_H=int((n_H_prev+2*pad-f)/stride+1) 26 n_W=int((n_W_prev+2*pad-f)/stride+1) 27 28 # Initialize the output volume Z with zeros. (≈1 line) 29 Z=np.zeros((m,n_H,n_W,n_C)) 30 31 # Create A_prev_pad by padding A_prev 32 A_prev_pad=zero_pad(A_prev, pad) 33 34 for i in range(m): # loop over the batch of training examples 35 a_prev_pad = A_prev_pad[i] # Select ith training example's padded activation 36 for h in range(n_H): # loop over vertical axis of the output volume 37 for w in range(n_W): # loop over horizontal axis of the output volume 38 for c in range(n_C): # loop over channels (= #filters) of the output volume 39 40 # Find the corners of the current "slice" (≈4 lines) 41 vert_start=h*stride #竖向,开始的位置 42 vert_end=vert_start+f #竖向,结束的位置 43 horiz_start=w*stride #横向,开始的位置 44 horiz_end=horiz_start+f #横向,结束的位置 45 # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line) 46 a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:] 47 # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line) 48 Z[i,h,w,c]=conv_single_step(a_slice_prev, W[:,:,:,c], b[0,0,0,c]) 49 ### END CODE HERE ### 50 51 # Making sure your output shape is correct 52 assert(Z.shape == (m, n_H, n_W, n_C)) 53 # Save information in "cache" for the backprop 54 cache = (A_prev, W, b, hparameters) 55 return Z, cache
池化层

1 def pool_forward(A_prev, hparameters, mode = "max"): 2 """ 3 Implements the forward pass of the pooling layer 4 5 Arguments: 6 A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) 7 hparameters -- python dictionary containing "f" and "stride" 8 mode -- the pooling mode you would like to use, defined as a string ("max" or "average") 9 10 Returns: 11 A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C) 12 cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters 13 """ 14 15 # Retrieve dimensions from the input shape 16 (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape 17 18 # Retrieve hyperparameters from "hparameters" 19 f = hparameters["f"] 20 stride = hparameters["stride"] 21 22 # Define the dimensions of the output 23 n_H = int(1 + (n_H_prev - f) / stride) 24 n_W = int(1 + (n_W_prev - f) / stride) 25 n_C = n_C_prev 26 27 # Initialize output matrix A 28 A = np.zeros((m, n_H, n_W, n_C)) 29 30 ### START CODE HERE ### 31 for i in range(m): # loop over the training examples 32 for h in range(n_H): # loop on the vertical axis of the output volume 33 for w in range(n_W): # loop on the horizontal axis of the output volume 34 for c in range (n_C): # loop over the channels of the output volume 35 36 # Find the corners of the current "slice" (≈4 lines) 37 vert_start = h * stride 38 vert_end = vert_start + f 39 horiz_start = w * stride 40 horiz_end = horiz_start + f 41 42 # Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line) 43 a_prev_slice = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] 44 45 # Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean. 46 if mode == "max": 47 A[i, h, w, c] = np.max(a_prev_slice) 48 elif mode == "average": 49 A[i, h, w, c] = np.mean(a_prev_slice) 50 ### END CODE HERE ### 51 52 # Store the input and hparameters in "cache" for pool_backward() 53 cache = (A_prev, hparameters) 54 # Making sure your output shape is correct 55 assert(A.shape == (m, n_H, n_W, n_C)) 56 return A, cache
卷积层的反向传播(选学)
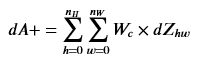
Wc是过滤器,dZhw是卷积层第h行第w列的使用点乘计算后的输出Z的梯度。
da_perv_pad[vert_start:vert_end,horiz_start:horiz_end,:] += W[:,:,:,c] * dZ[i,h,w,c]

dWc是一个过滤器的梯度,aslice是Zij的激活值
dW[:,:,:, c] += a_slice * dZ[i , h , w , c]
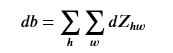
db[:,:,:,c] += dZ[ i, h, w, c]
1 def conv_backward(dZ, cache): 2 """ 3 Implement the backward propagation for a convolution function 4 5 Arguments: 6 dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C) 7 cache -- cache of values needed for the conv_backward(), output of conv_forward() 8 9 Returns: 10 dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev), 11 numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) 12 dW -- gradient of the cost with respect to the weights of the conv layer (W) 13 numpy array of shape (f, f, n_C_prev, n_C) 14 db -- gradient of the cost with respect to the biases of the conv layer (b) 15 numpy array of shape (1, 1, 1, n_C) 16 """ 17 ### START CODE HERE ### 18 # Retrieve information from "cache" 19 (A_prev, W, b, hparameters)=cache 20 # Retrieve dimensions from A_prev's shape 21 (m, n_H_prev, n_W_prev, n_C_prev)=A_prev.shape 22 # Retrieve dimensions from W's shape 23 (f, f, n_C_prev, n_C)=W.shape 24 # Retrieve information from "hparameters" 25 stride=hparameters['stride'] 26 pad=hparameters['pad'] 27 # Retrieve dimensions from dZ's shape 28 (m, n_H, n_W, n_C)=dZ.shape 29 30 # Initialize dA_prev, dW, db with the correct shapes 31 dA_prev=np.zeros((m, n_H_prev, n_W_prev, n_C_prev)) 32 dW=np.zeros((f, f, n_C_prev, n_C)) 33 db=np.zeros((1, 1, 1, n_C)) 34 35 # Pad A_prev and dA_prev 36 A_prev_pad=zero_pad(A_prev,pad) 37 dA_prev_pad=zero_pad(dA_prev, pad) 38 39 for i in range(m): # loop over the training examples 40 41 # select ith training example from A_prev_pad and dA_prev_pad 42 a_prev_pad = A_prev_pad[i] 43 da_prev_pad = dA_prev_pad[i] 44 45 for h in range(n_H): # loop over vertical axis of the output volume 46 for w in range(n_W): # loop over horizontal axis of the output volume 47 for c in range(n_C): # loop over the channels of the output volume 48 49 # Find the corners of the current "slice" 50 vert_start = h 51 vert_end = vert_start + f 52 horiz_start = w 53 horiz_end = horiz_start + f 54 55 # Use the corners to define the slice from a_prev_pad 56 a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] 57 # Update gradients for the window and the filter's parameters using the code formulas given above 58 da_prev_pad[vert_start:vert_end, horiz_start:horiz_end,:] += W[:,:,:,c] * dZ[i, h, w, c] 59 dW[:,:,:,c] += a_slice * dZ[i,h,w,c] 60 db[:,:,:,c] += dZ[i,h,w,c] 61 62 # Set the ith training example's dA_prev to the unpaded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :]) 63 dA_prev[i,:,:,:] = da_prev_pad[pad:-pad, pad:-pad, :] 64 ### END CODE HERE ### 65 66 # Making sure your output shape is correct 67 assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev)) 68 return dA_prev, dW, db
池化层的反向传播(选学)
创建掩码矩阵(保存最大值位置)
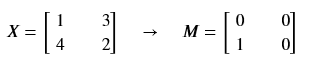
def create_mask_from_window(x): """ Creates a mask from an input matrix x, to identify the max entry of x. Arguments: x -- Array of shape (f, f) Returns: mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x. """ ### START CODE HERE ### (≈1 line) mask = x == np.max(x) ### END CODE HERE ### return mask
均值池化层的反向传播
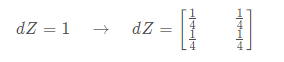
1 def distribute_value(dz, shape): 2 """ 3 Distributes the input value in the matrix of dimension shape 4 5 Arguments: 6 dz -- input scalar 7 shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz 8 9 Returns: 10 a -- Array of size (n_H, n_W) for which we distributed the value of dz 11 """ 12 13 ### START CODE HERE ### 14 # Retrieve dimensions from shape (≈1 line) 15 (n_H, n_W) = shape 16 17 # Compute the value to distribute on the matrix (≈1 line) 18 average = dz / (n_H * n_W) 19 20 # Create a matrix where every entry is the "average" value (≈1 line) 21 a = np.ones(shape) * average 22 ### END CODE HERE ### 23 24 return a
池化层的反向传播
1 def pool_backward(dA, cache, mode = "max"): 2 """ 3 Implements the backward pass of the pooling layer 4 5 Arguments: 6 dA -- gradient of cost with respect to the output of the pooling layer, same shape as A 7 cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters 8 mode -- the pooling mode you would like to use, defined as a string ("max" or "average") 9 10 Returns: 11 dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev 12 """ 13 ### START CODE HERE ### 14 # Retrieve information from cache (≈1 line) 15 (A_prev, hparameters) = cache 16 # Retrieve hyperparameters from "hparameters" (≈2 lines) 17 stride = hparameters["stride"] 18 f = hparameters["f"] 19 # Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines) 20 m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape 21 m, n_H, n_W, n_C = dA.shape 22 23 # Initialize dA_prev with zeros (≈1 line) 24 dA_prev = np.zeros(A_prev.shape) 25 26 for i in range(m): # loop over the training examples 27 # select training example from A_prev (≈1 line) 28 a_prev = A_prev[i] 29 for h in range(n_H): # loop on the vertical axis 30 for w in range(n_W): # loop on the horizontal axis 31 for c in range(n_C): # loop over the channels (depth) 32 # Find the corners of the current "slice" (≈4 lines) 33 vert_start = h 34 vert_end = vert_start + f 35 horiz_start = w 36 horiz_end = horiz_start + f 37 38 # Compute the backward propagation in both modes. 39 if mode == "max": 40 # Use the corners and "c" to define the current slice from a_prev (≈1 line) 41 a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c] 42 # Create the mask from a_prev_slice (≈1 line) 43 mask = create_mask_from_window(a_prev_slice) 44 # Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line) 45 dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += np.multiply(mask, dA[i, h, w, c]) 46 47 elif mode == "average": 48 # Get the value a from dA (≈1 line) 49 da = dA[i, h, w, c] 50 # Define the shape of the filter as fxf (≈1 line) 51 shape = (f, f) 52 # Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line) 53 dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += distribute_value(da, shape) 54 55 ### END CODE ### 56 57 # Making sure your output shape is correct 58 assert(dA_prev.shape == A_prev.shape) 59 return dA_prev