Kalman滤波在金融时间序列中的应用

清华大学交叉信息院博士在读

对于金融时间序列（如股票价格曲线等）的处理一直是人们关注的热点问题，为了更好地理解价格行为，一部分研究者引入了一些物理概念来对其进行描述，比如将价格走势与经典力学中的惯性、谐振、速度和加速度等概念联系起来，而接下来介绍的这篇文章就提出了一种结合物理概念后，利用Kalman滤波来分析价格时间序列的方法，利用该方法我们可以对价格序列进行去噪和预测。

论文中介绍的方法叫做Kinetic Component Analysis (KCA)，用一句话来说，这个方法就是把价格序列看作是一个随机过程，对其做泰勒展开后，再用Kalman滤波，从噪声中提取出我们想要的信号。接下来就详细介绍KCA方法。

Kalman滤波

首先介绍一下什么是Kalman滤波，它其实就是一个加权融合的方法，将不同方法得到的结果做加权平均，从而得到一个更精确的结果。这个描述可能比较抽象，接下来看一个具体的例子：

一枚导弹在空中飞行，在时刻t，其位置为 $x_t$ 、速度为 $v_t$ ，通过人为控制而产生加速度为 $a_t$ ，现在想要得到导弹在下一时刻t+1位置 $x_{t+1}$ 的估计。

首先要明确一点，无论采用什么方法，我们得到都只是导弹的估计位置，而真实位置是永远未知的。

1. 预测

在这里我们有两种方法来估计位置，第一种就是利用时刻t的位置、速度和加速度进行预测，根据物理知识，可知公式为：

${s}_{t+1}=As_t+Bu_t+w \$

其这个方程就是Kalman滤波中的预测方程，其中 ${s}_{t}=left[egin{array} {x}_{t} \ {v}_{t} end{array} ight]$ 是导弹在当前t时刻的真实状态， $u_t=a_t$ ；矩阵 ${A}_{}=left[egin{array}{ll} {1} & {Delta t} \ {0} & {1} end{array} ight]$ ，矩阵 ${B}=left[egin{array}{l} frac{Delta t^{2}}{2} \ {Delta t} end{array} ight]$ ； $w_{} sim N(0, Q)$ ，加上这一项是考虑到导弹在飞行过程中可能会受到如气流等外界因素的影响，因此真实状态 $s_{t+1}$ 应该还要加一点随机噪声，可以看出 $s_{t+1}$ 也是服从高斯分布的。

由于我们并不知道真实状态 $s_t$ ，所以我们只能用估计状态 $hat{s}_{t}=left[egin{array} hat{x}_{t} \ hat{v}_{t} end{array} ight]$ 来进行预测，有

$hat{s}_{t+1|t}=A hat{s}_t+Bu_t \$

其中 $hat{s}_{t+1|t}=left[egin{array} hat{x}_{t+1|t} \ hat{v}_{t+1|t} end{array} ight]$ 是方程的预测状态。可以看出，如果估计状态 $hat{s}_t$ 服从高斯分布的话，那么 $hat{s}_{t+1|t}$ 也同样服从高斯分布。

现在我们就要完全描述预测状态 $hat{s}_{t+1|t}$ 。我们知道，一个高斯分布用均值向量和协方差矩阵就可以完全描述。

均值向量比较简单，有 $E[hat{s}_{t+1|t}]=AE[ hat{s}_t]+Bu_t$

对于协方差矩阵，Kalman滤波一个很好的特点就是可以递推计算估计状态与真实状态之间的协方差，具体如下：

由前面的式子可知

$s_{t+1}-hat{s}_{t+1|t}=A(s_{t}-hat{s}_{t})+w \$

假设t时刻的估计状态与真实状态的协方差为 $P_{t}$ ，那么预测状态 $hat{s}_{t+1|t}$ 与真实状态 $s_{t+1}$ 之间的协方差 $P_{t+1|t}$ 为：

$egin{aligned} {P}_{t+1 | t} &=Eleft[left({s}_{t+1}-hat{{s}}_{t+1 | t} ight)left({s}_{t+1}-hat{{s}}_{t+1 | t} ight)^{T} ight] \ &=Eleft[left({A}left({s}_{t}-hat{{s}}_{t} ight)+omega_{} ight) cdotleft({A}left({s}_{t}-hat{{s}}_{t} ight)+omega_{} ight)^{T} ight] \ end{aligned}\$

考虑到状态向量与噪声 $w$ 是不相关的，那么原式就有

$egin{aligned} {P}_{t+1 | t} &=AEleft[left({s}_{t}-hat{{s}}_{t} ight)left({s}_{t}-hat{{s}}_{t} ight)^{T} ight]A^T+Eleft[ww^T ight] \ &=AP_{t}A^T+Q end{aligned}\$

综上所述，第一种方法预测出的结果 $hat{s}_{t+1|t}=left[egin{array} hat{x}_{t+1|t} \ hat{v}_{t+1|t} end{array} ight]$ ，其协方差矩阵 ${P}_{t+1 | t} =AP_{t}A^T+Q$ ，这样我们就完全描述了预测结果的概率分布。

2. 测量

第二种方法就是利用导弹上面自带的测距装置，该装置通过测量激光的传播时间来间接计算位置，测得传播时间为 $z_t$ ，乘以光速c就可以得到位置。不过考虑到仪器的精度问题，测量结果上应该是有噪声的，假设噪声为 $varepsilon_{} sim N(0, R)$ ，那么就有等式

$z_{t+1}=Hs_{t+1}+varepsilon \$

其中 $H=left[egin{array}{l} frac{1}{c} & {0} end{array} ight]$ 被叫做转换矩阵，该方程就是Kalman滤波中的测量方程，考虑到在t+1时刻进行测量时，导弹的真实状态已经确定，即真实状态 $s_{t+1}$ 是一固定向量，那么测量结果 $z_{t+1}$ 就是一个高斯分布，均值向量为 $E[z_{t+1}]=HE[s_{t+1}]$ ，协方差矩阵就是噪声的协方差 $R$ 。

3. 加权融合

对于预测和测量得到的两个结果 $hat{x}_{t+1|t}$ 和 $z_{t+1}$ ，更确切的说是两个分布，我们应该怎样得出一个最终的估计结果呢？

为了讨论简便，先考虑一维的情况。首先，由于 $hat{x}_{t+1|t}$ 和 $z_{t+1}$ 的度量分别是长度和时间，我们在这里先把度量都统一成时间，那么两结果的分布为：

预测分布： $y_{1}left(x ; mu_{1}, sigma_{1} ight)=frac{1}{sqrt{2 pileft(frac{sigma_{1}}{c} ight)^{2}}} e^{-frac{left(x-frac{mu_{1}}{c} ight)^{2}}{2left(frac{sigma_{1}}{c} ight)^{2}}} \$ 其中 $mu_1$ 和 $sigma_1^2$ 就是上面预测结果的均值向量和协方差矩阵 ${P}_{t+1 | t}$ 。
测量分布： $y_{2}left(x ; mu_{2}, sigma_{2} ight)=frac{1}{sqrt{2 pi sigma_{2}^{2}}} e^{-frac{left(x-u_{2} ight)^{2}}{2 sigma_{2}^{2}}} \$ 其中 $mu_2$ 和 $sigma_2^2$ 就是上面测量结果的均值向量和协方差矩阵 $R$ 。

为了得到一个综合结果，一个非常直观的方法就是把这两结果加权平均一下，我们可以把这两个分布相乘，由高斯分布的性质可知，两个高斯分布的乘积仍是一个高斯分布，这个新高斯分布的均值就可以看作是原来两个分布的均值按照各自方差的加权平均，而这个新高斯分布就是我们想要的加权平均结果，如下图所示。

经过计算，新分布 $Hhat{x}_{t+1}$ 的均值为：

$mu_{ ext{new}}=mu_1+K(mu_2-Hmu_1) \$

其中 $H=frac{1}{c}$ , $K=frac{H sigma_{1}^{2}}{H^{2} sigma_{1}^{2}+sigma_{2}^{2}}$

方差为：

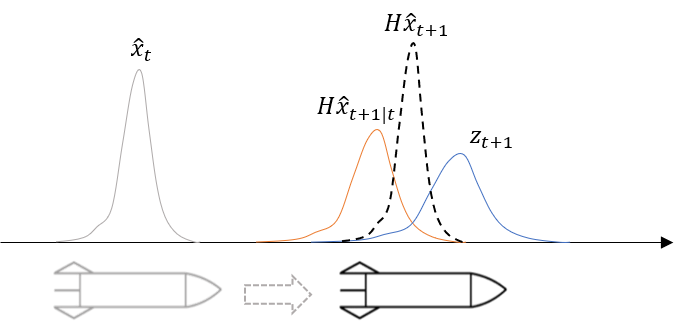
$sigma_{ ext {new}}^{2}=sigma_{1}^{2}-frac{frac{sigma_{1}^{2}}{c}}{left(frac{sigma_{1}}{c} ight)^{2}+sigma_{2}^{2}} cdot frac{sigma_{1}^{2}}{c}=sigma_{1}^{2}-K H sigma_{1} \$

这样我们就用Kalman滤波求出了对于t+1时刻状态的估计，得到了 $hat{s}_{t+1}$ 之后，就可以继续对之后状态进行估计，这就是Kalman滤波的完整过程。

4. 普遍形式

上面是一维情况下的Kalman滤波，高维情况也比较类似，只不过要写成矩阵形式，具体如下：

$hat{s}_{t+1|t}=A hat{s}_t+Bu_t \ hat{s}_{t+1}=hat{s}_{t+1|t}+K_{t+1}(z_{t+1}-H_{t+1}hat{s}_{t+1|t})\ egin{aligned} {P}_{t+1 | t} &= AP_{t}A^T+Qend{aligned}\P_{t+1}=P_{t+1|t}-K_{t+1}H_{t+1}P_{t+1|t}$

其中 $K_{t+1}=H_{t+1}P_{t+1|t}cdot(H_{t+1}P_{t+1|t}H_{t+1}^T+R)^{-1}$ ，被叫做Kalman增益。

上述省略了部分推导，感兴趣的同学可以参看这篇文章或者其它相关材料。

将Kalman滤波用于金融时间序列

介绍完背景知识之后，接下来进入正题。在这里我们以股票价格为例。我们知道股票价格具有一定的随机性，但它也并不完全是布朗运动，在一些因素的影响下，股票价格有时也会呈现出一些整体的趋势，论文中把这样的趋势叫做“金融惯性”。

考虑到股票的这两个特性，设价格序列为 $P(t)$ ，我们可以将其分解成：

$P(t) = p(t)+b(t) \$

其中 $p(t)$ 是连续且二阶可微的，它代表了股票价格中的“基本成分”，实际反映了价格的走势；而 $b(t)$ 则是噪声，它导致了股票价格具有随机性，对于价格走势没有意义。

通过这样的角度来看股票价格问题，我们发现每次观察到的价格 $P(t)$ 其实是价格走势 $p(t)$ 加上一个噪声 $b(t)$ 得到的。这样就可将它对应到上面介绍的Kalman滤波问题，股票价格 $P(t)$ 其实就是测量值 $z_t$ ， $p(t)$ 其实就是真实状态 $s_t$ 。现在我们就利用Kalman滤波来得到一个关于价格走势 $p(t)$ 的估计，即实现对于价格序列 $P(t)$ 的去噪。

对于 $p(t)$ ，做二阶泰勒展开有

$egin{aligned} p(t) &=pleft(t_{0} ight)+left.frac{partial p(t)}{partial t} ight|_{t=t_{0}}left(t-t_{0} ight)+left.frac{1}{2} frac{partial^{2} p(t)}{partial t^{2}} ight|_{t=t_{0}}left(t-t_{0} ight)^{2} \ &+left.sum_{n=3}^{infty} frac{1}{n !} frac{partial^{n} p(t)}{partial t^{n}} ight|_{t=t_{0}}left(t-t_{0} ight)^{n} end{aligned} \$

忽略掉后面的高阶小量，并把时间离散化，有

$p_{t} approx p_{t-1}+v_{t-1} h+frac{1}{2} a_{t-1} h^{2} \$

其中 $vleft(t_{0} ight)=left.frac{partial p(t)}{partial t} ight|_{t=t_{0}}$ 可以看做速度， $aleft(t_{0} ight)=left.frac{partial^{2} p(t)}{partial t^{2}} ight|_{t=t_{0}}=left.frac{partial v(t)}{partial t} ight|_{t=t_{0}}$ 可以看做加速度， $h$ 是时间步。

类似于上面的导弹问题，Kalman滤波的预测和测量方程可以分别写为：

$egin{aligned} s_{t}=& A s_{t-1}+B u_{t-1}+w_{} \ & z_{t}=H s_{t}+varepsilon_{} end{aligned} \$

其中状态 $s_{t}=left[egin{array} {p}_{t} \ {v}_{t} \ a_{t}end{array} ight]$ ， $A=left[egin{array}{ccc} {1} & {h} & {frac{1}{2} h^{2}} \ {0} & {1} & {h} \ {0} & {0} & {1} end{array} ight]$ ， $w_{} sim N(0, Q)$ ， $H=left[egin{array}{l} {1} & {0} & {0}end{array} ight]$ ， $varepsilon_{} sim N(0, R)$ 也就是上面价格序列的 $b(t)$ 。

这里需要注意一下， $B u_{t-1}$ 这一项在导弹问题中代表了外界对于导弹的影响，放在股票中也类似，代表了外界对于股票的影响。在一般情况下，作为股票的观察者，我们基本无法影响股票走势，这时该项可以省去；不过对于一些特殊情况（如大型交易商、大型股东等），外界影响存在，这一项就有存在的必要。

按照Kalman滤波的方法，运用上面的那些公式，我们就可以根据测量值 $z_t$ ，得到估计状态 $s_t$ ，即去除噪生后的价格走势 $p(t)$ 。

EM算法估计最优参数

问题到这里好像就已经解决了，然而其实还有一个非常关键的问题，别的参数都知道了，可是两个正态噪声 $w$ 和 $varepsilon_{}$ 的协方差矩阵Q和R（R是1×1协方差矩阵，也就是方差）却并不知道，而这两个参数是至关重要的，因为它们决定了加权平均的结果，只有找到合适的值，最终估计结果的去噪效果才会好。在这里，我们采用了EM算法来估计Q和R。

EM算法又名期望最大化算法（Expectation Maximization Algorithm），是一个在概率模型中寻找参数最大似然估计的算法，其中概率模型依赖于无法直接观测的隐变量。该算法是一个迭代算法，一次迭代分为两步：求期望和最大化，即E步和M步：

E步：根据参数计算隐变量的估计值，并利用它计算关于测量值的似然估计。
M步：将参数值最大化为在E步上求得的最大似然值，更新参数值。

M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行，直到收敛。

放在这个问题中，价格趋势 $p(t)$ 就是上面提到的隐变量，而E步就是先通过现有的Q和R计算出 $p(t)$ 的估计值，然后再得到关于测量值 $z$ 的似然估计值；M步就是将原参数Q和R更新为最大化似然估计值的参数。这样不断地迭代就可以得到极大似然估计的参数，也就是最优的参数。

现在来看具体流程：

E步：

对于参数 $Q$ 和 $R$ ，照搬之前的Kalman滤波公式： $hat{s}_{t+1|t}=A hat{s}_t+Bu_t \ hat{s}_{t+1}=hat{s}_{t+1|t}+K_{t+1}(z_{t+1}-H_{t+1}hat{s}_{t+1|t})\ {P}_{t+1 | t} = AP_{t}A^T+Q \ P_{t+1}=P_{t+1|t}-K_{t+1}H_{t+1}P_{t+1|t}$

其中 $K_{t+1}=H_{t+1}P_{t+1|t}cdot(H_{t+1}P_{t+1|t}H_{t+1}^T+R_{})^{-1}$

其中 $hat{s}_{t}=left[egin{array} {hat{p}}_{t} \ {hat{v}}_{t} \ hat{a}_{t}end{array} ight]$ 就可以计算得到隐变量的估计值 $hat{p}_t$ ，然后就可以进行根据测量值 $z_t$ 进行似然估计：

$egin{aligned} L(Q,R) &=P(hat{s}_0)cdotprod_{t=1}^{n} P(hat{s}_t|hat{s}_{t-1}) cdot P(z_t|hat{s}_{t})\ &=Sigma^{-frac{1}{2}}e^{frac{1}{2}(hat{s}_0-mu)^TSigma^{-1}(hat{s}_0-mu)} \ &quadcdotprod_{t=1}^{n}Q^{-frac{n}{2}}e^{frac{1}{2}(hat{s}_t-Ahat{s}_{t-1}-Bhat{u}_{t-1})^TQ^{-1}(hat{s}_t-Ahat{s}_{t-1}-Bhat{u}_{t-1})} \ &quadcdot R^{-frac{n}{2}}e^{frac{1}{2}(hat{z}_t-Hhat{s}_{t})^T R^{-1} (hat{z}_t-Hhat{s}_{t})} end{aligned} \$

简单解释一下这个式子，n为时间长度，在一个时刻t，我们知道估计值 $hat{s}_t$ 的分布是正态分布，而且 $hat{s}_t$ 是由 $hat{s}_{t-1}$ 得到的，那么只看t时刻的似然估计就为：

$Q^{-frac{1}{2}}e^{frac{1}{2}(hat{s}_t-Ahat{s}_{t-1}-Bhat{u}_{t-1})^TQ^{-1}(hat{s}_t-Ahat{s}_{t-1}-Bhat{u}_{t-1})} cdot R^{-frac{1}{2}}e^{frac{1}{2}(hat{z}_t-Hhat{s}_{t})^T R^{-1} (hat{z}_t-Hhat{s}_{t})} \$

在这里忽略了一些常数，其实就是两个正态分布概率密度的乘积，也就是 $P(hat{s}_t|hat{s}_{t-1}) cdot P(z_t|hat{s}_{t})$ ，这是一个给定 $hat{s}_{t-1}$ 的条件概率，那么我们令t从1到n做一个连乘，再乘一个初始0时刻的概率分布 $P(hat{s}_0)$ （这个概率分布是我们提前给定的，服从 $N(mu,Sigma)$ ），就得到了对于整个测量序列 ${z_t ,t=1...n}$ 的似然估计，也就是上面那个式子。

M步：

接下来就是常规操作，最大化对数似然估计值，得到新的参数 $Q'$ 和 $R'$ ，即

$(Q',R'):=argmaxlimits_{Q,R}(log L(Q,R))\$

我们可以通过求解方程 $frac{partial log L}{partial Q}=frac{partial log L}{partial R}=0$ 来得到满足要求的参数。

这样就完成了一次迭代，将M步得到的参数 $Q'$ 和 $R'$ 作为E步的输入，不断迭代，就可以得到最优的参数，这样我们就通过EM算法估计到了最优的协方差矩阵Q和R。

其实，我们并不是一定要用EM算法，由于估计值 $hat{s}_t$ 是参数Q和R的函数，所以可以直接一步到位，直接用极大似然估计去得到参数Q和R，这在理论上是可行的，但是求解的方程是非线性的，实际情况中得到方程的解并不容易。而EM算法的优点就是通过分成E步和M步的方式，使得在M步求解的方程是线性的，这是因为已经在E步中算出了 $hat{s}_t$ 的值，它在M步中是一个定值，这就使得方程 $frac{partial log L}{partial Q}=frac{partial log L}{partial R}=0$ 变为线性的，从而大大减小了求解难度。

实验对比

最后看一下该方法和一些常见去噪方法的对比实验

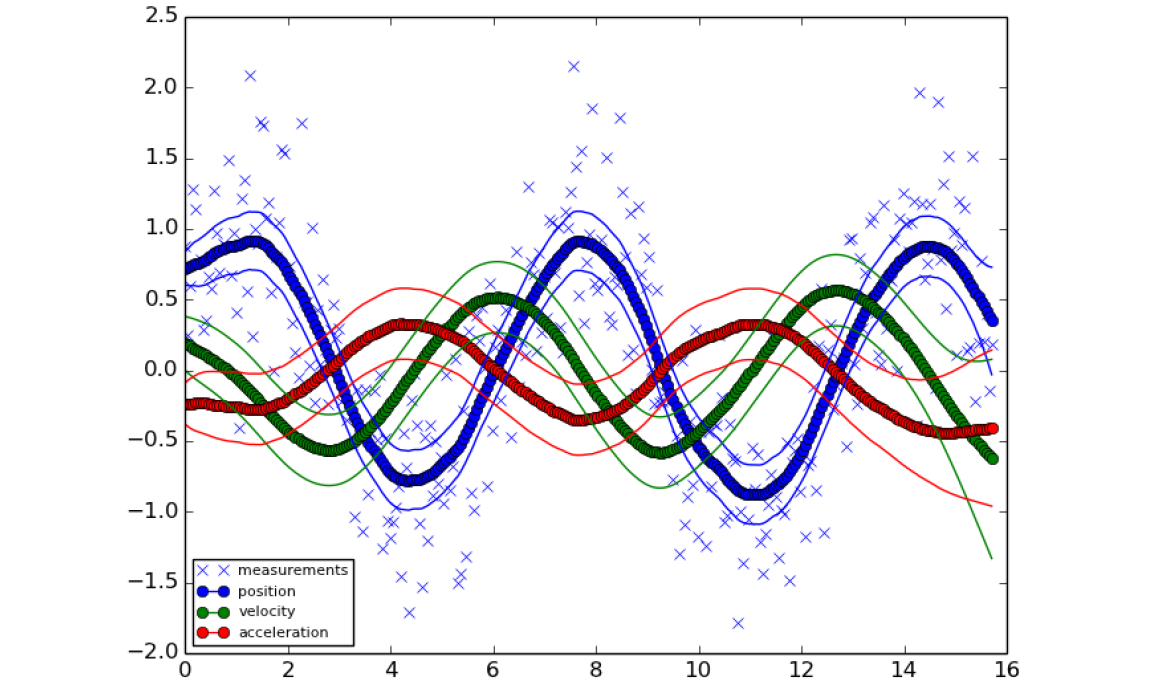
实验中的信号是通过在一个正弦信号上加噪声得到的，论文中的KCA方法在这个信号上面的效果如下图所示

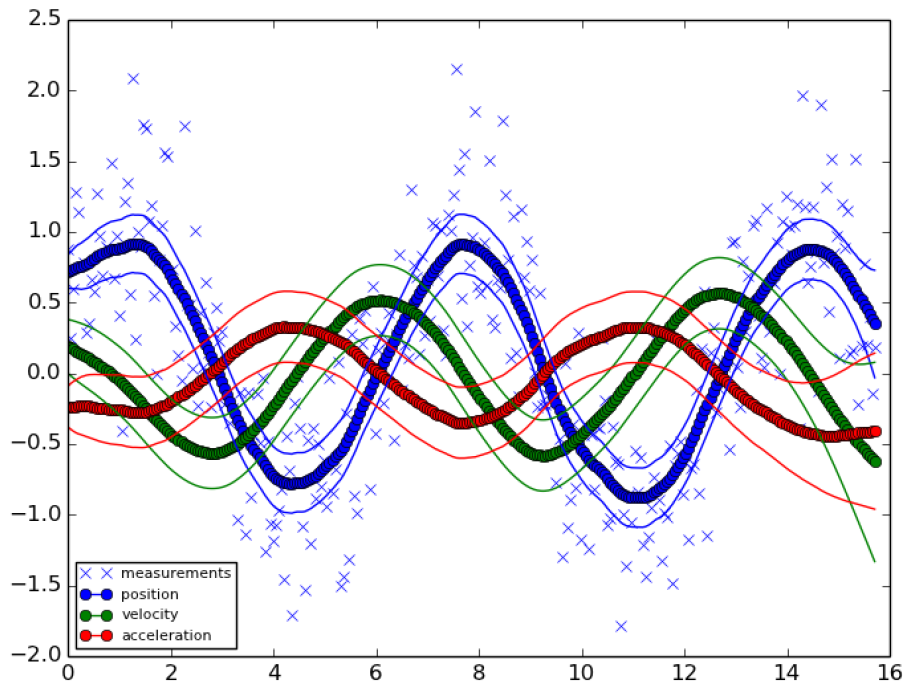Kalman滤波结果（均值线和置信区间）

可以看到，KCA不仅能够给出估计值，还能够给出其置信区间（因为有协方差 $P_t$ ）。下面是KCA与我们熟知的傅里叶(FFT)滤波方法的对比

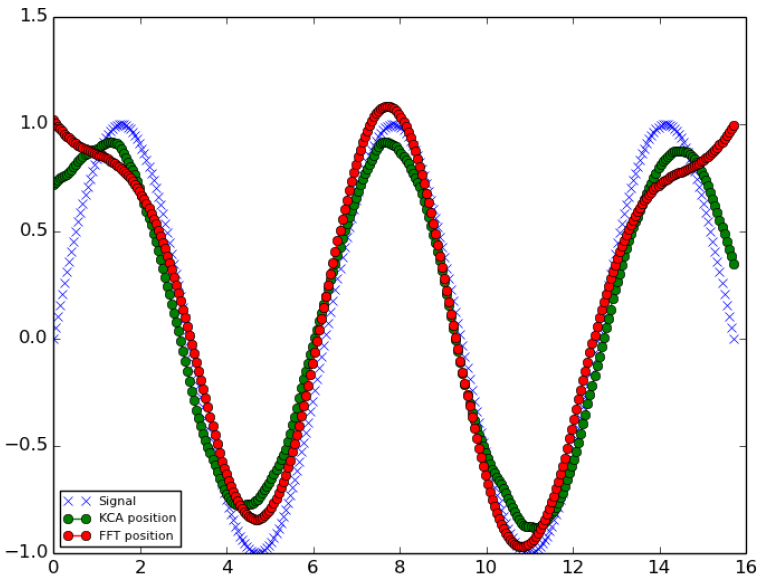
通过对比，KCA滤波主要有三个优点：

KCA提供信号位置的点估计和置信区间估计，而FFT只提供点估计。
除了位置状态，KCA还显示了关于速度和加速度的信息。
在边界处，KCA估计的信号更接近真实信号。这个优点很重要，因为研究人员通常对推断或预测信号感兴趣，这就要求最新时刻的估计越准确越好，我们可以看到KCA在右边界处的估计结果明显比FFT更好。

除了FFT以外，论文与局部加权回归 (LOWESS)方法做了对比，它是一种利用数据的局部子集来拟合加权线性回归，来实现去噪的方法，结果如下：

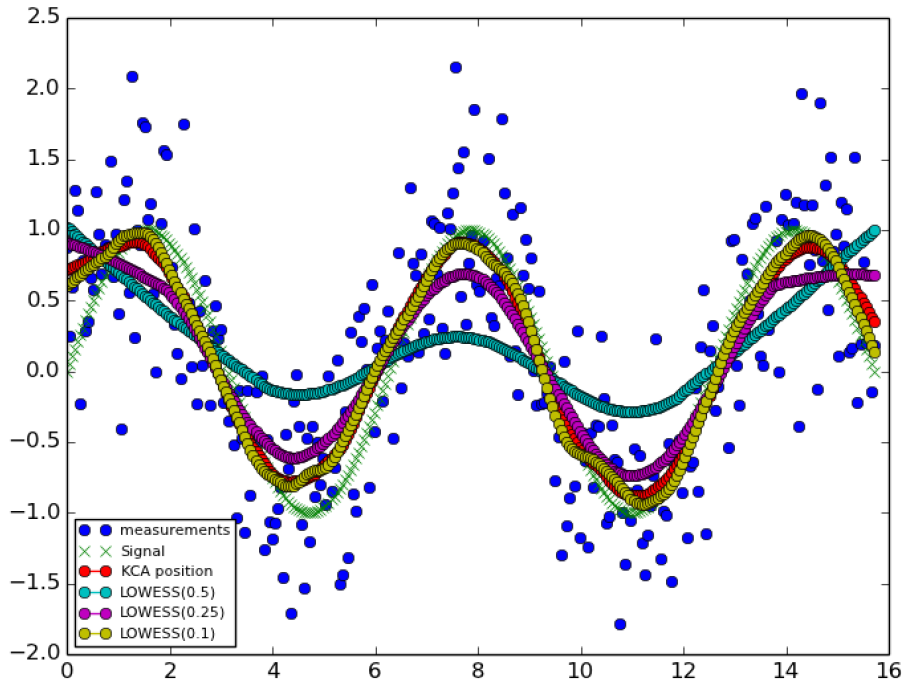
图中的LOWESS(0.5)代表用了50%的数据来做局部回归，与LOWESS相比，KCA具有如下优势：

LOWESS不具备生成预测的能力，因为每个估计都高度依赖于相邻的样本(样本前后都有)。而KCA一种前瞻性的方法，对序列结构的变化具有很强的鲁棒性。
LOWESS的每一次估计都需要一个样本子集，这使得它需要大量的计算。而KCA只需要知道最近的一个状态就可以做出估计。

总结

这篇论文将金融序列的随机性认为是存在测量噪声的缘故，所以应用了Kalman滤波来实现对于噪声背后的价格趋势的估计。不过我个人认为的这个假设有一点问题，论文中认为价格是由连续且二阶可微的 $p(t)$ 和噪声 $h(t)$ 相加得到的，并认为价格趋势 $p(t)$ 对应着Kalman滤波中的真实状态，然而在Kalman滤波中，真实状态的预测方程是 $s_{t}= A s_{t-1}+B u_{t-1}+w_{}$ ，这意味着真实状态，即价格趋势中包含着噪声 $w$ ，这就与前面二阶可微的假设相冲突了，所以感觉这里有些矛盾。

参考资料

[1] KINETIC COMPONENT ANALYSIS

[2] AN APPROACH TO TIME SERIES SMOOTHING AND FORECASTING USING THE EM ALGORITHM

[3] 卡尔曼滤波：从入门到精通

编辑于 2020-01-11

时间序列的单调性

张戎发表于数学人生

时间序列与回归预测（二）

SCP-173

（三十九）通俗易懂理解——卡尔曼滤波与扩展卡尔曼滤波

网上的资料永远都是参差不齐，经典的卡尔曼滤波让我折腾好久都没完全搞懂，现在总算找到点门路，特此记录下，后附原文来源。利用卡尔曼滤波我们可以做什么？我们举一个玩具的栗子：你开…

梦里寻梦发表于通俗易懂理...

图解卡尔曼滤波器，无需深厚的数学知识也易懂（第二部分：数学基础背景知识补充）

potat...发表于《视觉SL...

写下你的评论...

「已注销」3 个月前

网站流量异常点检测是否也可以使用卡尔曼滤波？
段易通 (作者) 回复「已注销」3 个月前

不好意思，我对网站流量异常点检测不了解，所以回答不了您的问题。在我个人看来，卡尔曼滤波就是一个在动力学框架下的去噪过程，所以若常规去噪方法可以用在异常点检测上面的话，那么卡尔曼滤波也可以一试。

另外，考虑到卡尔曼滤波是建立在动力学框架上的，所以如果网络流量可以建模成一个动力学过程的话，那卡尔曼滤波的效果可能会更好（前提是去噪方法可以用在异常点检测上）。
Jia Guo回复「已注销」3 个月前

基于Kalman filter的故障诊断策略

宁静致远3 个月前

w理解为因为公式描述的不精确导致的误差就不会有矛盾了吧
段易通 (作者) 回复宁静致远3 个月前

您说的对，我也认为w是由于预测方程的不精确导致的。
不过我感觉矛盾在于导弹问题和股票问题的不一致，导弹问题中存在着两种噪声（预测方程不准确导致的w，和测量时产生的epsilon），而股票问题只有一种噪声b(t) ，这就导致两个问题无法很好地对应起来。
按照论文的意思，股票的b(t)对应的应该是epsilon，这样的话价格趋势p(t)就对应导弹的真实状态，由于p(t)二阶可导的限制，那噪声w就应该为0，但是这就意味着预测方程是精确的，那么价格趋势p(t)是一个二次函数，而这显然不符合实际情况，我认为的矛盾就在这里。
宁静致远回复段易通 (作者)3 个月前

我认为股票问题应该也对应两种噪声，b(t)对应着市场噪声，w对应着假设p(t)二阶可导产生的误差，因为真实的p(t)公式不可知，假设它连续的，用泰勒级数展开，并截取前二阶，所以这个p(t)就不是精确的。

《Kalman滤波在金融时间序列中的应用》