多跳阅读理解——CogQA模型浅析
在nlp领域中,机器阅读理解一直是我们非常关心的一个问题,虽然BERT等模型在阅读理解任务上的表现很不错,但是这些任务大多比较简单。而本文介绍的这篇ACL 2019的论文,则从一个非常新颖的角度来研究机器的多跳阅读理解问题,并且取得了非常亮眼的表现。
多跳阅读理解
在介绍模型之前,先简单说一下什么是多跳阅读理解,顾名思义,就是有多次“跳转”的阅读理解问题,如下图所示。
 多跳阅读理解
多跳阅读理解
对于图中这样的问题,我们是没有办法直接给出答案的,因为它给出的信息都是一些间接的信息,问题问的是电影导演是谁,但是却没有给出电影的名字,而是给了一些关于取景地点和拍摄时间的信息。面对这样的问题,通常我们的做法就是先从知识库(如维基百科)中找到关于Quality Cafe这个实体的信息,看看有哪些电影在这里取过景,得到了Old School和Gone in 60 Seconds两个实体,然后再根据2003等时间信息进行进一步的筛选,找到满足问题要求的答案,即Todd Phillips。可以看出,对于这样的问题,需要经历多次“跳转”才能找到答案,所以叫做多跳阅读理解问题,这样的问题相对于单跳问题无疑更加复杂,而下文介绍的认知图谱问答(Cognitive Graph QA)模型就是针对于这样的问题设计的。
模型框架
通过上文,我们可以将回答多跳问题归纳为这样的过程,首先我们需要找到句子中的相关实体,例如上文中的Quality Cafe;然后通过对于问题中相关信息的分析推断,从这些实体中找到答案。在认知学中,有一个著名的“双过程理论(dual process theory)”它认为这里面其实有两种思维过程,对于“找到相关实体”而言,这是一种基于直觉的、无意识的过程,被叫做系统1;而对于“对信息进行分析推断”而言,这是一种通过推理来实现的过程,被叫做系统2,这就是人类的认知过程。
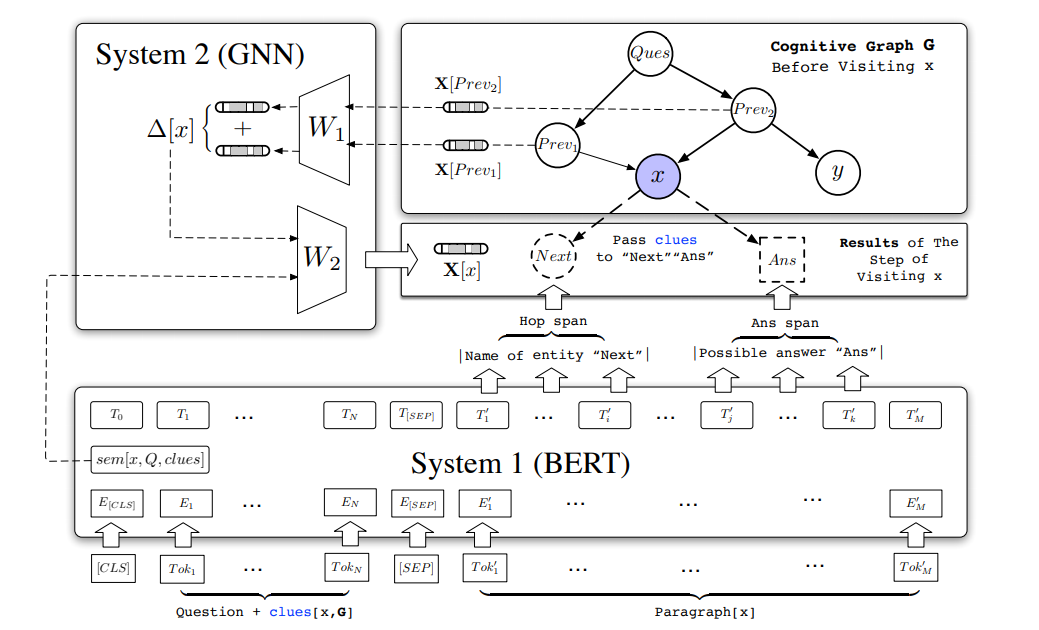
CogQA模型就采用了这样的思路,该模型按照双过程理论的思路,设计了系统1和2两个模块,系统1采用的是BERT模型,而系统2则采用图神经网络(GNN)模型。系统1的作用就是隐式地从句子中提取相关实体并对其中的信息进行编码,然后将它们提供给系统2;而系统2的作用则是将这些实体及其编码信息构建为一张认知图谱,通过图来对这些相关信息进行推理计算,同时指导系统1进行实体提取。模型架构如下:

图中的红框部分就是系统1,而蓝框部分就是系统2。这个模型看起来有些复杂,下面就分别通过系统1和2来对模型进行具体的介绍。
System 1(BERT)
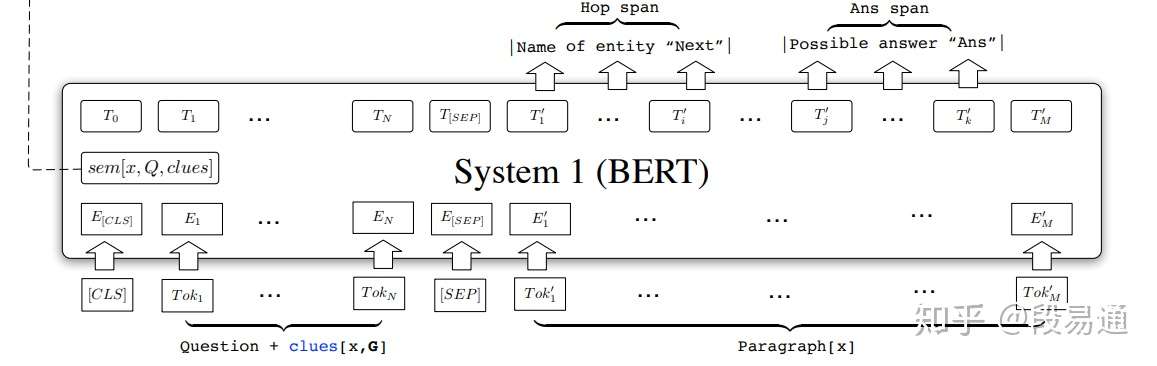 系统1结构
系统1结构
由于BERT模型在实体关系提取等nlp下游任务上表现很出色,因此系统1采用了BERT模型,它的输入由下面几部分组成:
其中question就是原始的问题句子,而 则是之前的文档中提到实体x的句子,例如若实体x是Old School,那么
则是在关于Quality Cafe的维基百科中涉及到Old School的句子,看了下文之后我们就知道,
其实就来自于实体节点x的前续节点;而最后一部分输入
其实就是关于实体x的维基百科文档。
现在来看系统1的输出,主要由三部分组成,首先是“下一跳实体名称(Hop span)”和“答案候选(Ans span)”,这两个输出都是从 中提取出来的,之所以要这样分成两部分,是因为Ans span通常都是与问题中的某些词相关的,例如where应该对应地名,而Hop span则复杂一些,它会更多地考虑与句子的关联程度。具体方法是对于BERT输出的序列T,通过四个可学习的指针向量
、
、
和
,计算该序列位置是实体开头或结尾的概率,形式如下:
这其实就是在BERT模型上分别加了四个单层神经网络和一个softmax层。另外,在这里我们先选出概率最大的k个起始位置 ,然后在实体最大长度maxL的限制下确定结束位置
,如下所示:
虽然选出来了句子中相对概率最大的k个起始位置,但这些实体可能实际的概率值都很小,与问题并不相关,因此还需要对它们进行筛选。由于在BERT模型中,第0个位置的token,即[CLS],通常用来表征句子中的所有输入token,所以在这里让 来作为一个阈值,只有大于它,才能被认为是Ans span,而Hop span也同样类似。
最后一部分输出是 ,它主要是关于
的语义向量,还是考虑到BERT模型输出的
有总结整个句子的能力,因此仍然利用
来表示
,只不过不是最后一层,作者在实验中发现倒数第三层的
效果最好,因此用它来作为语义向量
,而这个语义向量的作用将在下面的系统2部分介绍。
System 2(GNN)
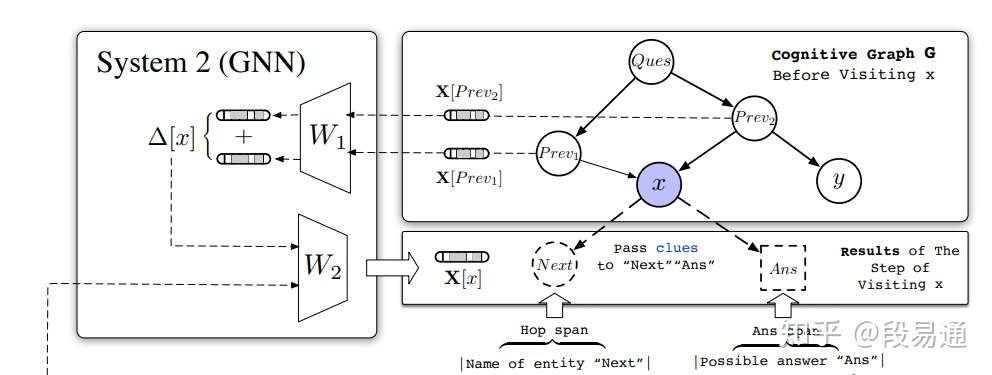
看到这里,可能你对于系统1还有很多疑问,比如系统1的那些输出到底是用来做什么,而系统2就回答了这个问题,它们都是用来生成一张由实体组成的认知图谱。系统2其实就是一个图神经网络(GNN),系统1输出的每一个Hop span和Ans span,都会在GNN上生成一个新的节点,新节点名字就是实体名称,然后再生成从原实体节点到新的下一跳实体节点的边,而系统1输出的 则用来初始化节点x的隐藏表示
。
不过,对于实体节点x,仅仅只有系统1输出的来作为隐藏表示是不够的,我们希望模型能够通过图谱中的这些信息进行“推理计算”,换言之就是让这些节点中包含的信息不只局限于本身,还能够受到其它相关节点的影响,例如对于Todd Phillips这个实体节点,我们想要的不只是它维基百科的语义信息,还有它与Old School和Quality Cafe之间的关系,这就需要它们之间的信息传递,而GNN就可以帮助我们来实现这样的关系推理,而这也是模型中的核心部分。
前面已经提到了,节点x的隐藏表示 通过
来初始化,而其更新规则如下:
其中,矩阵 和
是权重矩阵,A是图的邻接矩阵,D是A的度矩阵(degree matrix),
,
是对A的归一化,
是激活函数。
对于上式可以这样理解,左乘 就是计算与x的前续节点对x影响的累和,也就是
,然后再令x加上外部影响
,也就得到了新的隐藏表示
。GNN就是通过图谱中前续节点到下一跳节点信息传递的方式来实现关系推理。
这样一来,系统1不断地提取出一些相关实体及其语义信息,然后系统2用它们来对图进行扩展和填充,这样就可以得到一张关于这个阅读理解问题的认知图谱,图谱里面都是与这个问题直接或间接相关的实体节点,这样我们就能从中找出最合适的来作为答案,具体公式如下,其中 是一个两层的全连接神经网络。
模型整体流程如下:
 算法流程
算法流程
可以看出,模型是通过系统1和系统2之间的不断迭代的方式来扩展认知图谱的,系统1不断地为系统2中的认知图谱生成新的节点,而系统2则不断地为系统1提供线索信息 ,最终算法流程借助前沿点(frontier nodes)队列形式实现,每一个新的hop span都会进入队列,等待系统1对其文档进行实体的提取。需要注意的是,作为答案候选,ans spans并不会参与下一步跳转,所以不会进入frontier nodes。
模型训练
模型的训练一共分为两大部分,分别是针对系统1和系统2的训练部分。对于系统1,训练集中的样本标签就是hop span和ans span的位置,用 来表示,模型规定了每次输出的ans span只有一个,那
就是一个one-hot向量,即
,则损失函数如下:
对于hop span,输出可以为k个,则 ,损失函数形式一致。另外,为了提高模型的区分能力,可以将一些与问题不相关的实体节点提前加入图谱中,对于这样的样本,我们不希望系统1从中提取出实体,考虑到上文中采用了[CLS]的输出
来作为过滤阈值,因此对于这样不相关的负样本,令
,这样就可以提高阈值的过滤能力,对负样本而言无法输出hop span和ans span,从而提高模型的区分能力。
对于系统2,同样地,为了提高模型性能,需要加入一些负样本节点,它们由上面提到的负hop span节点和一些随机选择的ans span组成,损失函数的计算方式如下,
其中 是真正答案节点的one-hot向量。该损失函数除了可以用来优化预测器
和系统2的GNN以外,由于系统1输出的
也参与了GNN的计算,该损失函数还能用来微调(fine-tune)系统1的BERT模型。
实验
CogQA模型在多跳阅读理解问题上具有非常明显的优势,如下表所示。

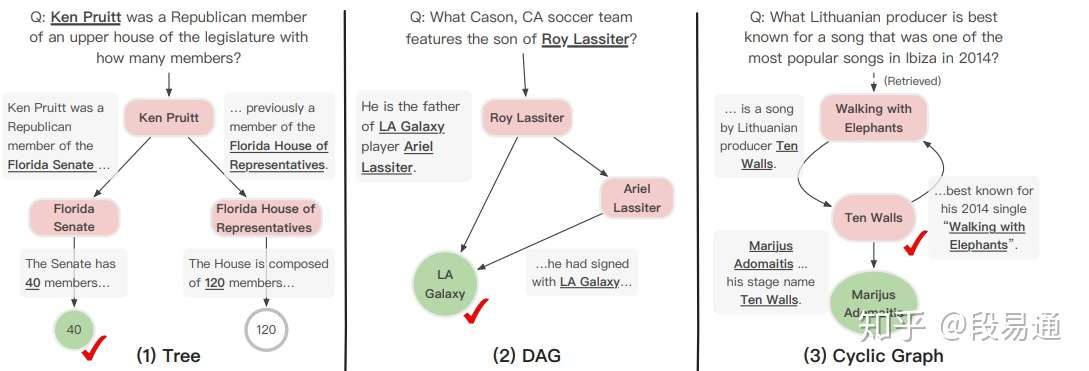
下面是一些具体的例子,从这些案例可以看出模型的推理过程。对于(1),模型是通过Senate与upper house之前的语义相似性做出的选择;对于(2),模型通过两条不同的路径得到了相同的答案,增加了答案的可靠性;对于(3),如果检查认知图谱会发现Ten Walls不过是Marijus Adomaitis的艺名,虽然问题中并没有提到任何实体,但是模型却给出了一个更加准确的答案。
总结
CogQA模型通过模拟人类的认知方式来解决机器的阅读理解问题,不仅利用了BERT模型强大的隐式关系提取的能力,还很好地利用图神经网络(GNN)实现了对于相关信息的显式推理。该模型的贡献不仅有解决机器的多跳阅读理解问题,还有对于模型推理过程的可解释性,借助模型生成的认知图谱,我们可以很容易地看到机器的推理过程,这样就使得模型不再是一个“黑盒子”,相信这也会为人们之后的研究带来一些启发。
参考资料
[1] Cognitive Graph for Multi-Hop Reading Comprehension at Scale