算法思想:
算法通过最小化约束条件4ac-b^2 = 1,最小化距离误差。利用最小二乘法进行求解,首先引入拉格朗日乘子算法获得等式组,然后求解等式组得到最优的拟合椭圆。
算法的优点:
a、椭圆的特异性,在任何噪声或者遮挡的情况下都会给出一个有用的结果;
b、不变性,对数据的Euclidean变换具有不变性,即数据进行一系列的Euclidean变换也不会导致拟合结果的不同;
c、对噪声具有很高的鲁棒性;
d、计算高效性。
算法原理:

代码实现(Matlab):
1 % 2 function a = fitellipse(X,Y) 3 4 % FITELLIPSE Least-squares fit of ellipse to 2D points. 5 % A = FITELLIPSE(X,Y) returns the parameters of the best-fit 6 % ellipse to 2D points (X,Y). 7 % The returned vector A contains the center, radii, and orientation 8 % of the ellipse, stored as (Cx, Cy, Rx, Ry, theta_radians) 9 % 10 % Authors: Andrew Fitzgibbon, Maurizio Pilu, Bob Fisher 11 % Reference: "Direct Least Squares Fitting of Ellipses", IEEE T-PAMI, 1999 12 % 13 % @Article{Fitzgibbon99, 14 % author = "Fitzgibbon, A.~W.and Pilu, M. and Fisher, R.~B.", 15 % title = "Direct least-squares fitting of ellipses", 16 % journal = pami, 17 % year = 1999, 18 % volume = 21, 19 % number = 5, 20 % month = may, 21 % pages = "476--480" 22 % } 23 % 24 % This is a more bulletproof version than that in the paper, incorporating 25 % scaling to reduce roundoff error, correction of behaviour when the input 26 % data are on a perfect hyperbola, and returns the geometric parameters 27 % of the ellipse, rather than the coefficients of the quadratic form. 28 % 29 % Example: Run fitellipse without any arguments to get a demo 30 if nargin == 0 31 % Create an ellipse 32 t = linspace(0,2); 33 34 Rx = 300; 35 Ry = 200; 36 Cx = 250; 37 Cy = 150; 38 Rotation = .4; % Radians 39 40 NoiseLevel = .5; % Will add Gaussian noise of this std.dev. to points 41 42 x = Rx * cos(t); 43 y = Ry * sin(t); 44 nx = x*cos(Rotation)-y*sin(Rotation) + Cx + randn(size(t))*NoiseLevel; 45 ny = x*sin(Rotation)+y*cos(Rotation) + Cy + randn(size(t))*NoiseLevel; 46 47 % Clear figure 48 clf 49 % Draw it 50 plot(nx,ny,'o'); 51 % Show the window 52 figure(gcf) 53 % Fit it 54 params = fitellipse(nx,ny); 55 % Note it may return (Rotation - pi/2) and swapped radii, this is fine. 56 Given = round([Cx Cy Rx Ry Rotation*180]) 57 Returned = round(params.*[1 1 1 1 180]) 58 59 % Draw the returned ellipse 60 t = linspace(0,pi*2); 61 x = params(3) * cos(t); 62 y = params(4) * sin(t); 63 nx = x*cos(params(5))-y*sin(params(5)) + params(1); 64 ny = x*sin(params(5))+y*cos(params(5)) + params(2); 65 hold on 66 plot(nx,ny,'r-') 67 68 return 69 end 70 71 % normalize data 72 mx = mean(X); 73 my = mean(Y); 74 sx = (max(X)-min(X))/2; 75 sy = (max(Y)-min(Y))/2; 76 77 x = (X-mx)/sx; 78 y = (Y-my)/sy; 79 80 % Force to column vectors 81 x = x(:); 82 y = y(:); 83 84 % Build design matrix 85 D = [ x.*x x.*y y.*y x y ones(size(x)) ]; 86 87 % Build scatter matrix 88 S = D'*D; 89 90 % Build 6x6 constraint matrix 91 C(6,6) = 0; C(1,3) = -2; C(2,2) = 1; C(3,1) = -2; 92 93 % Solve eigensystem 94 if 0 95 % Old way, numerically unstable if not implemented in matlab 96 [gevec, geval] = eig(S,C); 97 98 % Find the negative eigenvalue 99 I = find(real(diag(geval)) < 1e-8 & ~isinf(diag(geval))); 100 101 % Extract eigenvector corresponding to negative eigenvalue 102 A = real(gevec(:,I)); 103 else 104 % New way, numerically stabler in C [gevec, geval] = eig(S,C); 105 106 % Break into blocks 107 tmpA = S(1:3,1:3); 108 tmpB = S(1:3,4:6); 109 tmpC = S(4:6,4:6); 110 tmpD = C(1:3,1:3); 111 tmpE = inv(tmpC)*tmpB'; 112 [evec_x, eval_x] = eig(inv(tmpD) * (tmpA - tmpB*tmpE)); 113 114 % Find the positive (as det(tmpD) < 0) eigenvalue 115 I = find(real(diag(eval_x)) < 1e-8 & ~isinf(diag(eval_x))); 116 117 % Extract eigenvector corresponding to negative eigenvalue 118 A = real(evec_x(:,I)); 119 120 % Recover the bottom half... 121 evec_y = -tmpE * A; 122 A = [A; evec_y]; 123 end 124 125 % unnormalize 126 par = [ 127 A(1)*sy*sy, ... 128 A(2)*sx*sy, ... 129 A(3)*sx*sx, ... 130 -2*A(1)*sy*sy*mx - A(2)*sx*sy*my + A(4)*sx*sy*sy, ... 131 -A(2)*sx*sy*mx - 2*A(3)*sx*sx*my + A(5)*sx*sx*sy, ... 132 A(1)*sy*sy*mx*mx + A(2)*sx*sy*mx*my + A(3)*sx*sx*my*my ... 133 - A(4)*sx*sy*sy*mx - A(5)*sx*sx*sy*my ... 134 + A(6)*sx*sx*sy*sy ... 135 ]'; 136 137 % Convert to geometric radii, and centers 138 139 thetarad = 0.5*atan2(par(2),par(1) - par(3)); 140 cost = cos(thetarad); 141 sint = sin(thetarad); 142 sin_squared = sint.*sint; 143 cos_squared = cost.*cost; 144 cos_sin = sint .* cost; 145 146 Ao = par(6); 147 Au = par(4) .* cost + par(5) .* sint; 148 Av = - par(4) .* sint + par(5) .* cost; 149 Auu = par(1) .* cos_squared + par(3) .* sin_squared + par(2) .* cos_sin; 150 Avv = par(1) .* sin_squared + par(3) .* cos_squared - par(2) .* cos_sin; 151 152 % ROTATED = [Ao Au Av Auu Avv] 153 154 tuCentre = - Au./(2.*Auu); 155 tvCentre = - Av./(2.*Avv); 156 wCentre = Ao - Auu.*tuCentre.*tuCentre - Avv.*tvCentre.*tvCentre; 157 158 uCentre = tuCentre .* cost - tvCentre .* sint; 159 vCentre = tuCentre .* sint + tvCentre .* cost; 160 161 Ru = -wCentre./Auu; 162 Rv = -wCentre./Avv; 163 164 Ru = sqrt(abs(Ru)).*sign(Ru); 165 Rv = sqrt(abs(Rv)).*sign(Rv); 166 167 a = [uCentre, vCentre, Ru, Rv, thetarad];
实验效果:
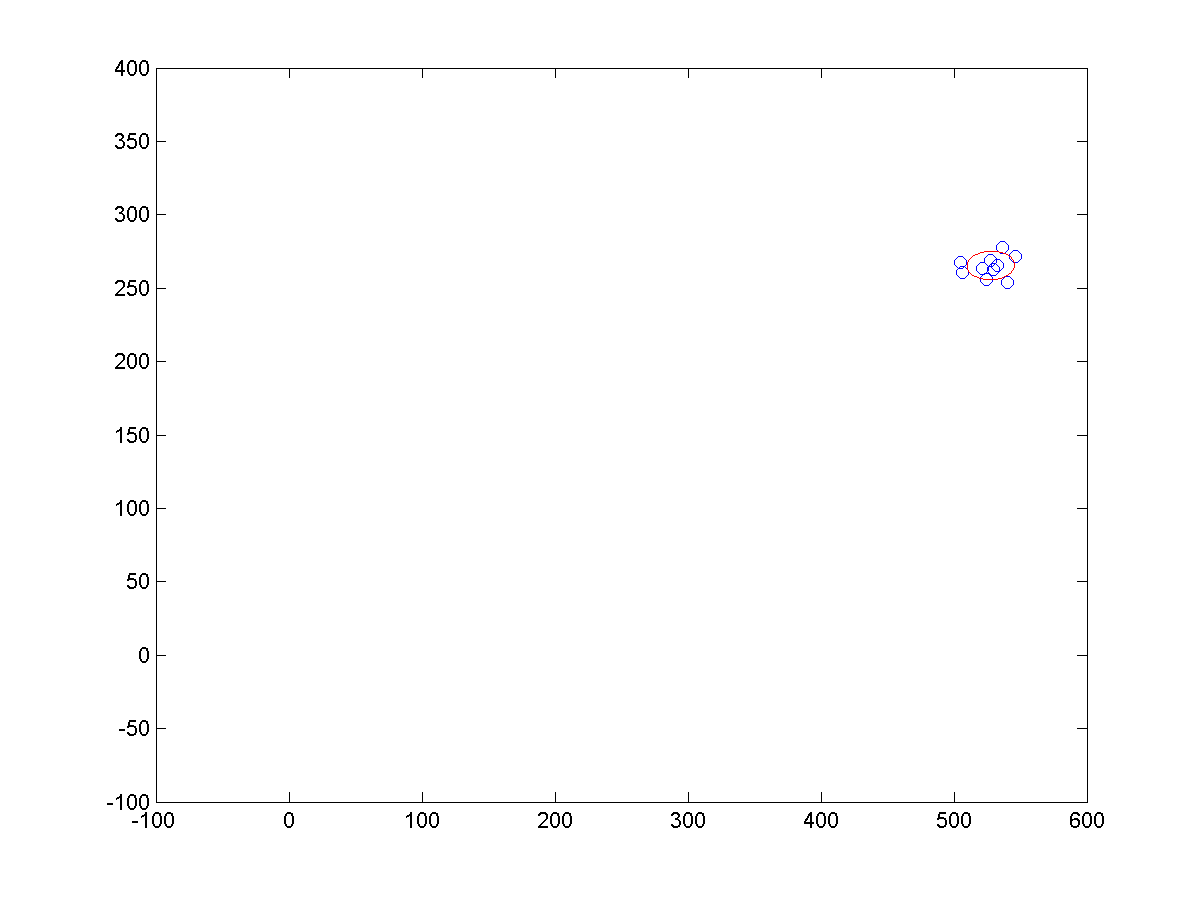
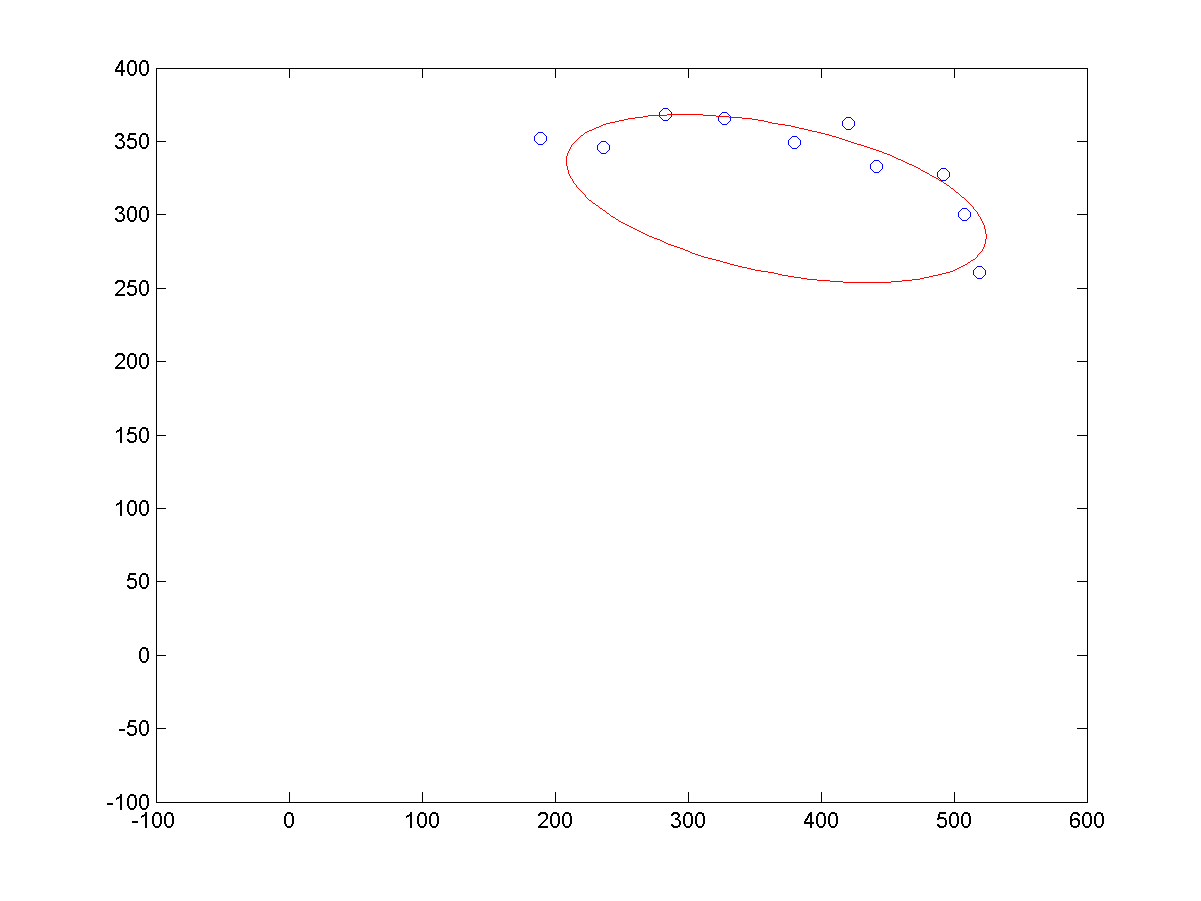
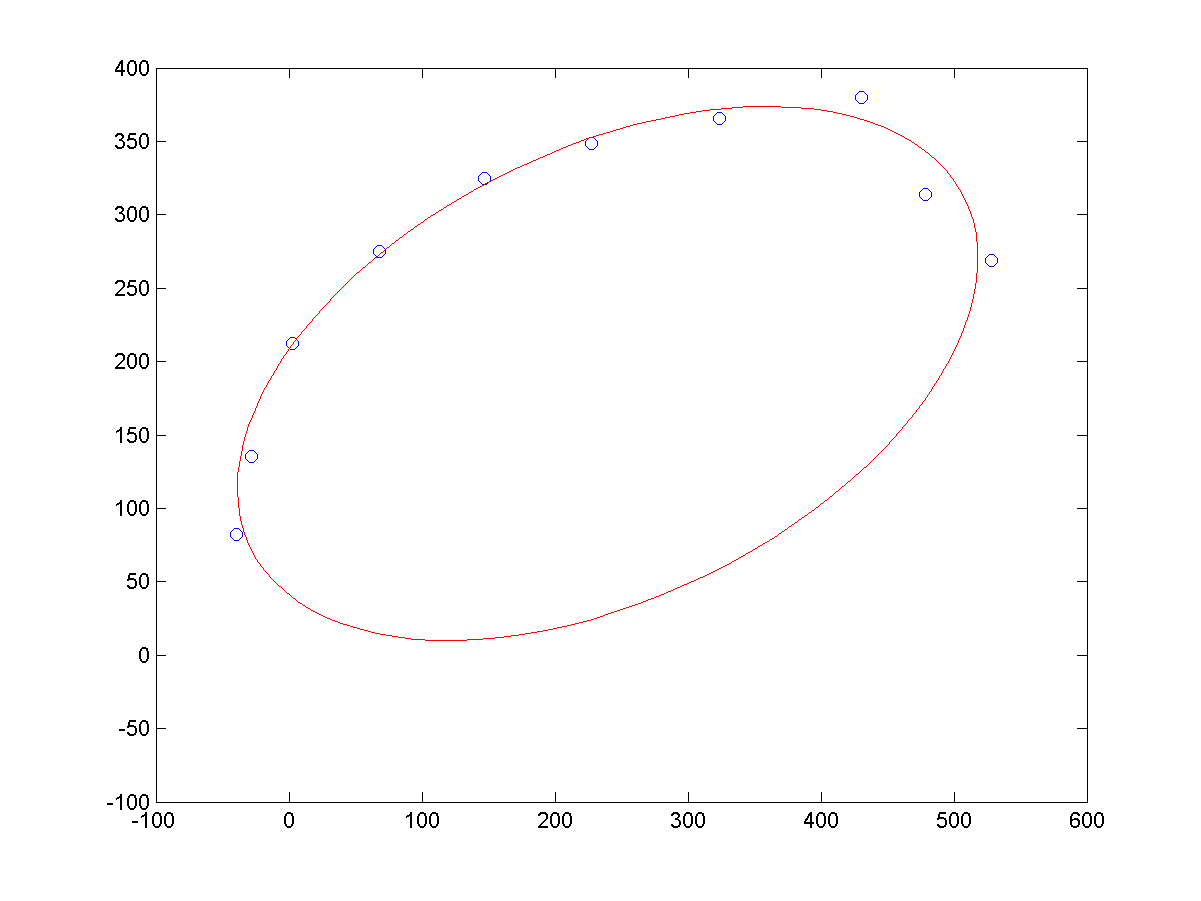
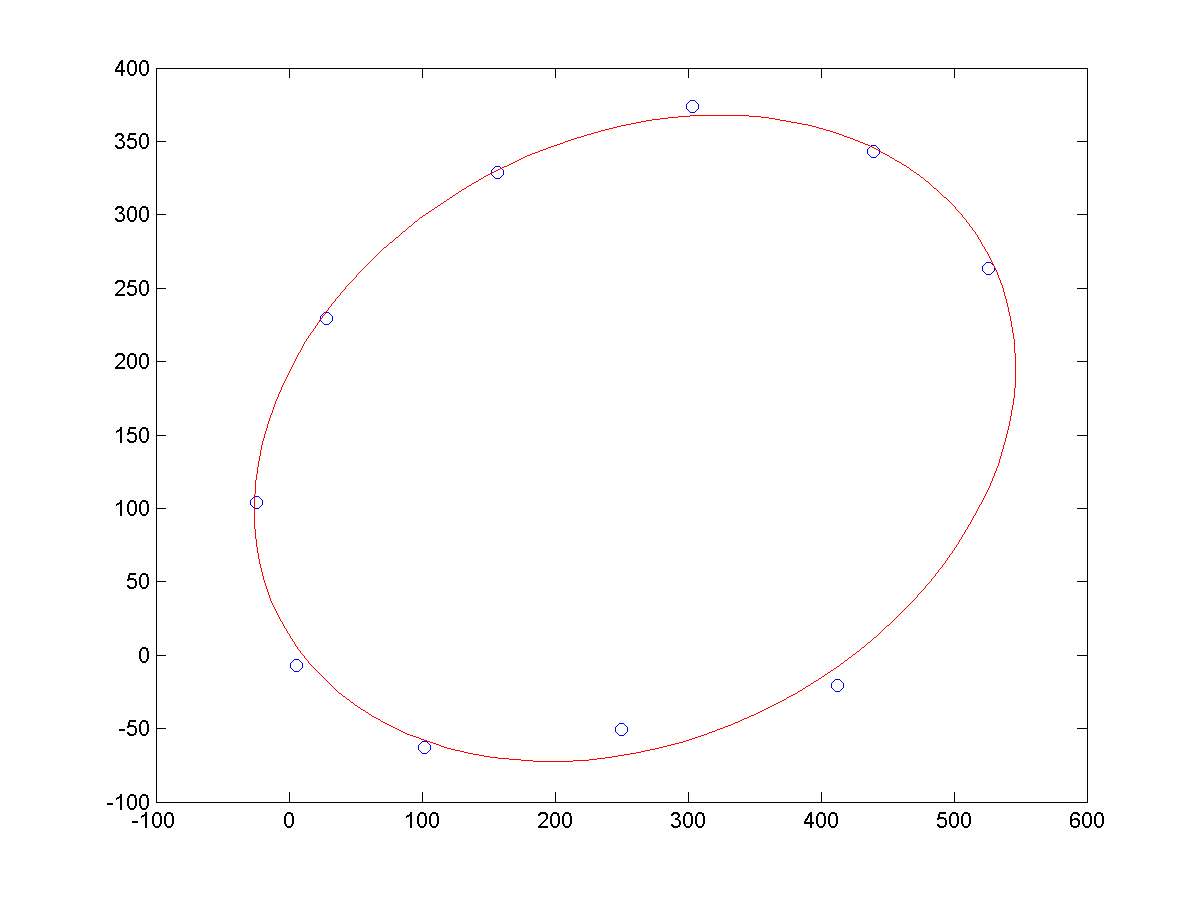
a、同等噪声条件下,不同长度的样本点,导致的拟合结果,如下所示:


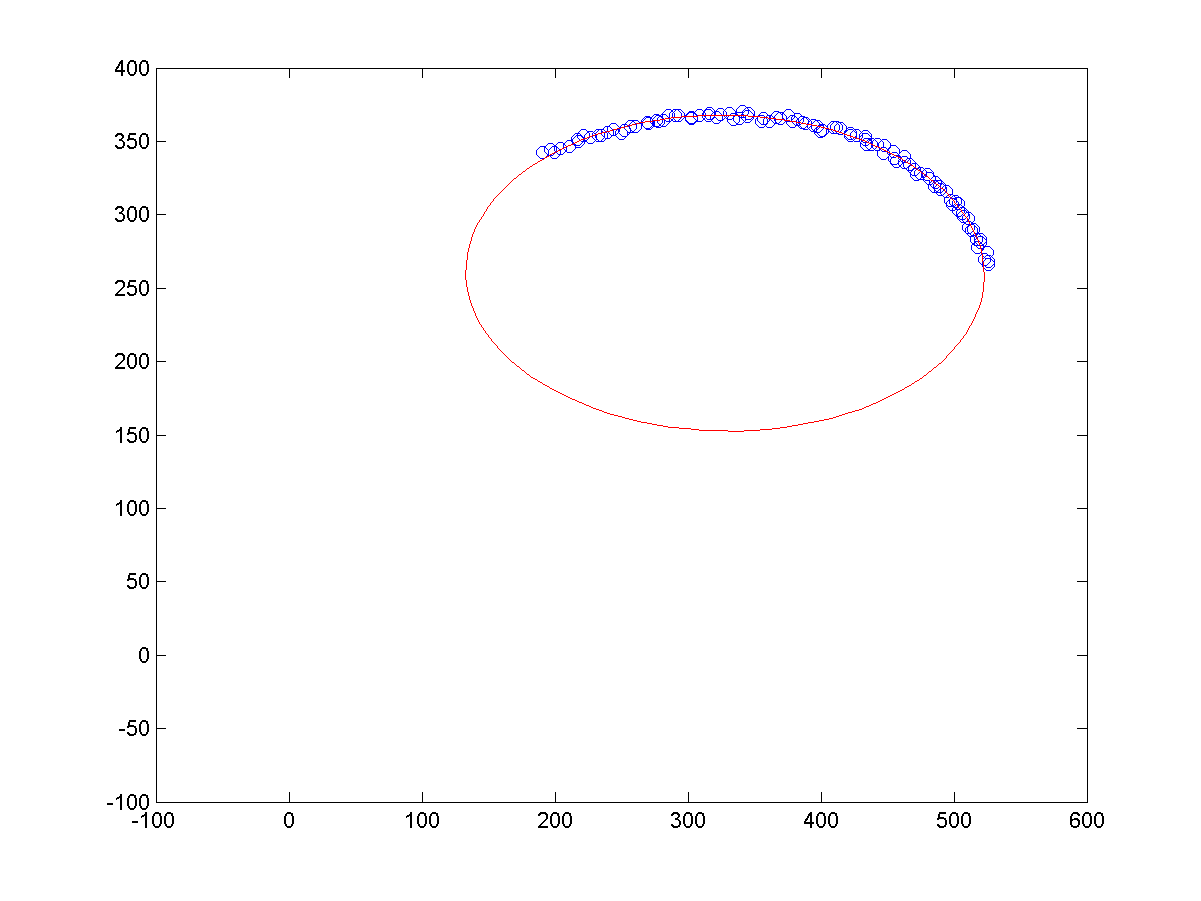
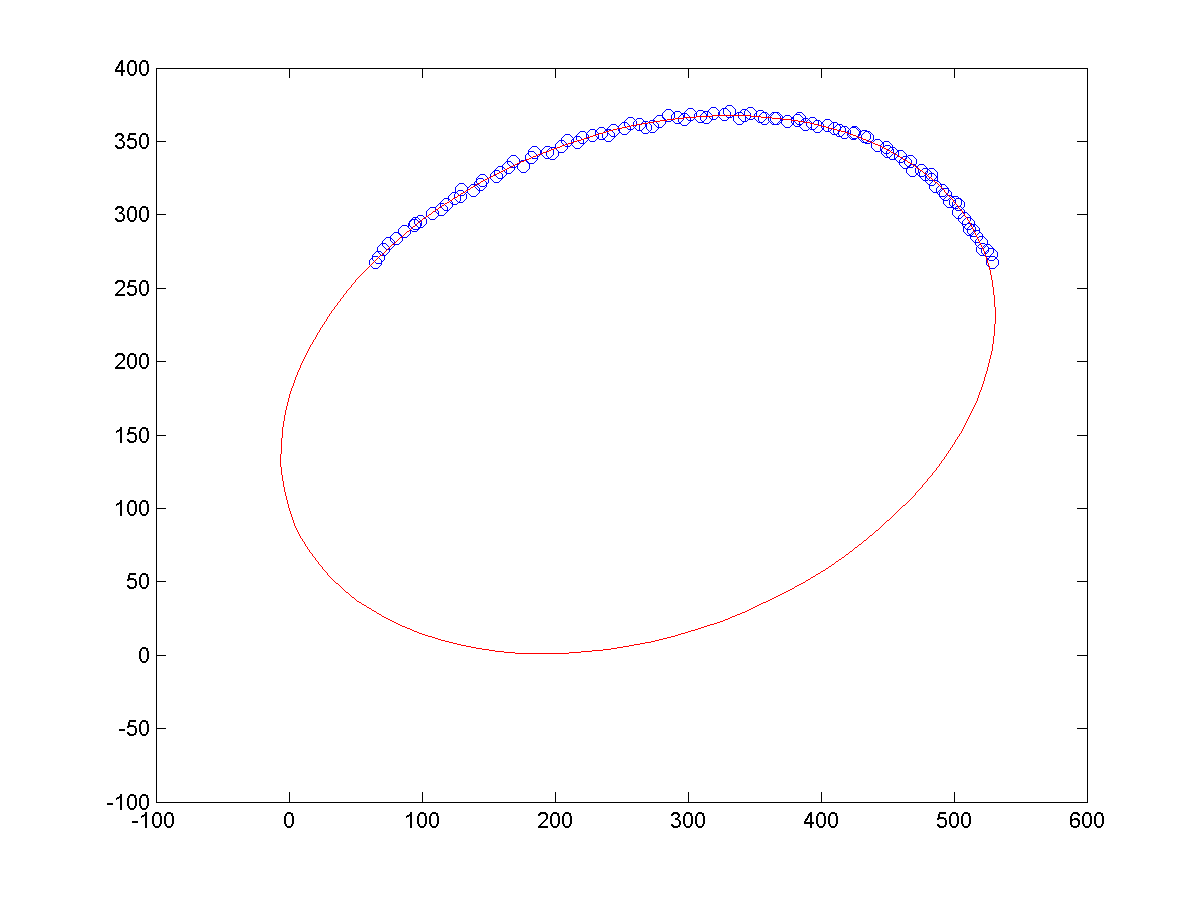
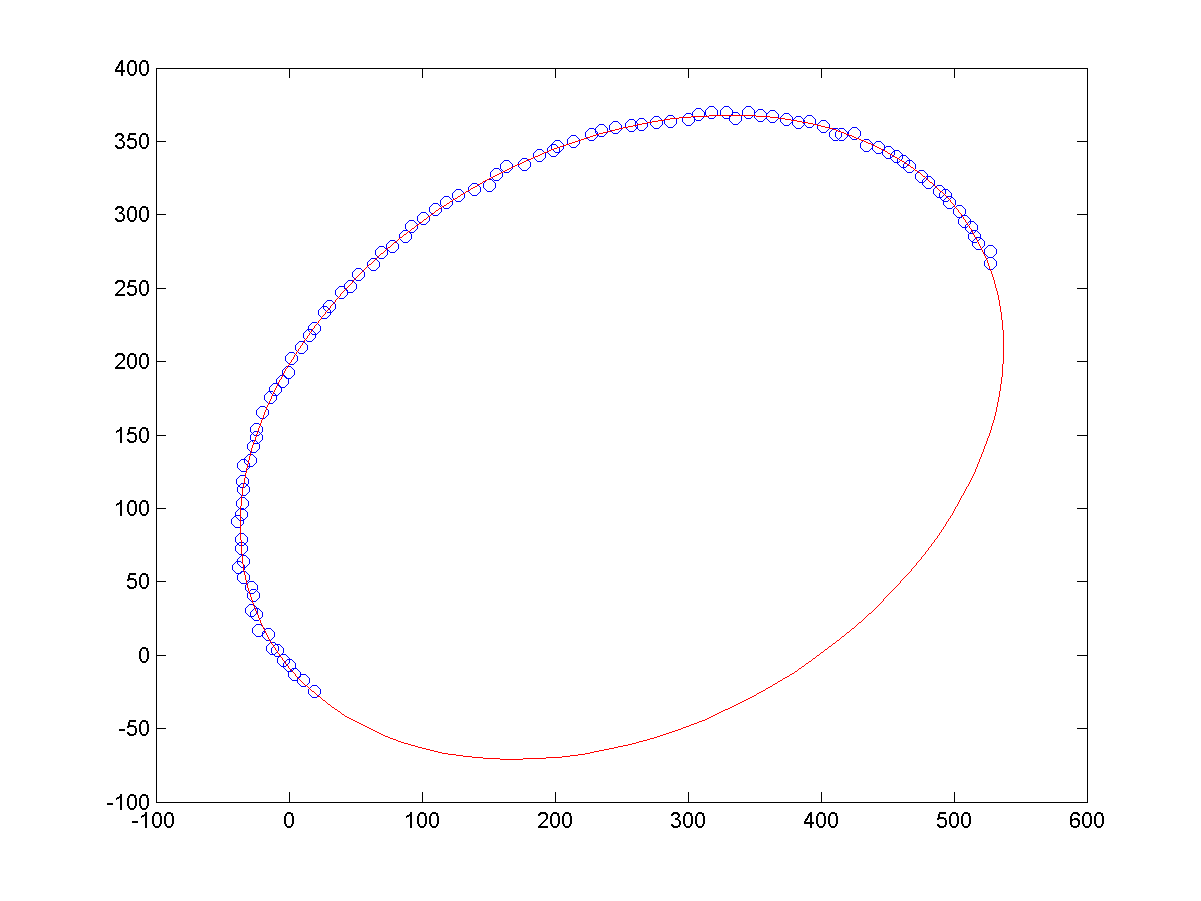
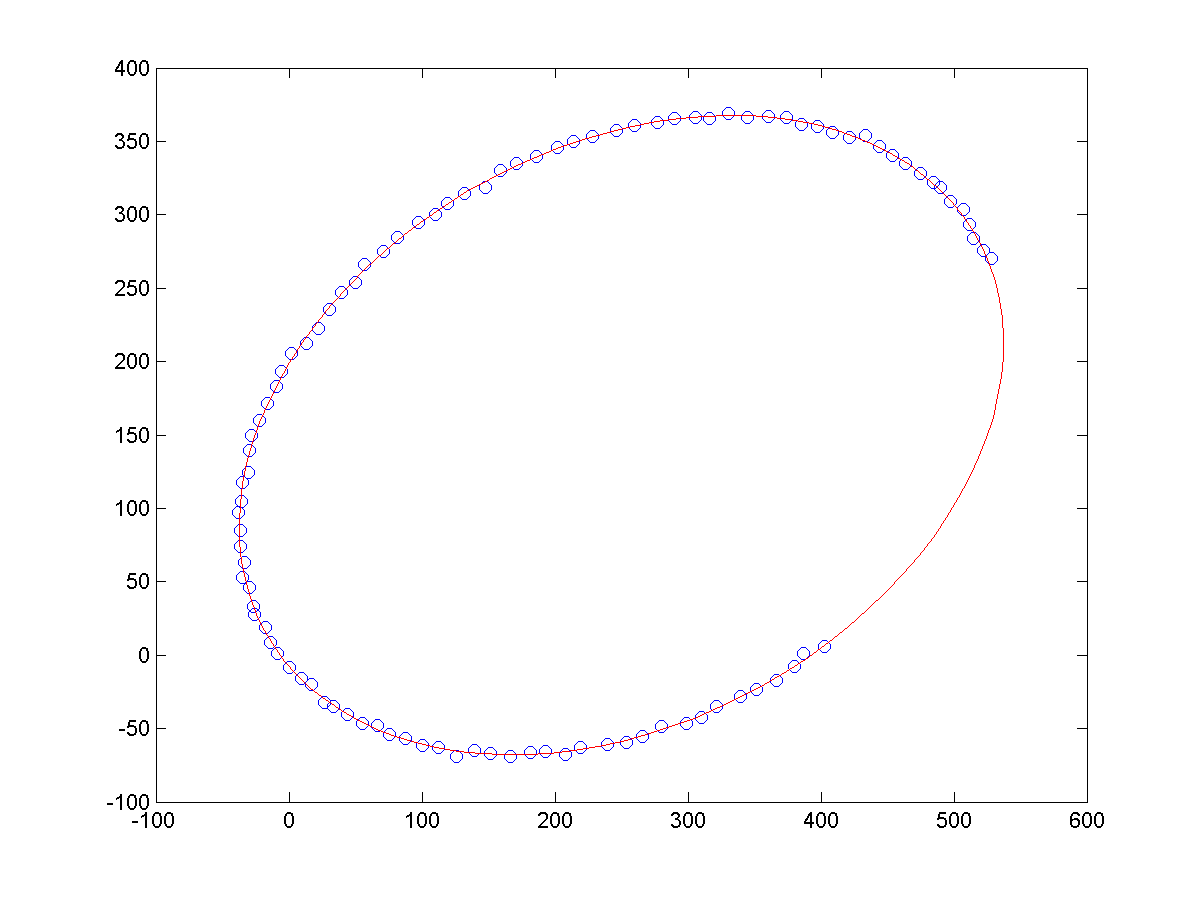
b、相同长度的样本点下,不同噪声的样本点,导致的拟合结果,如下所示:
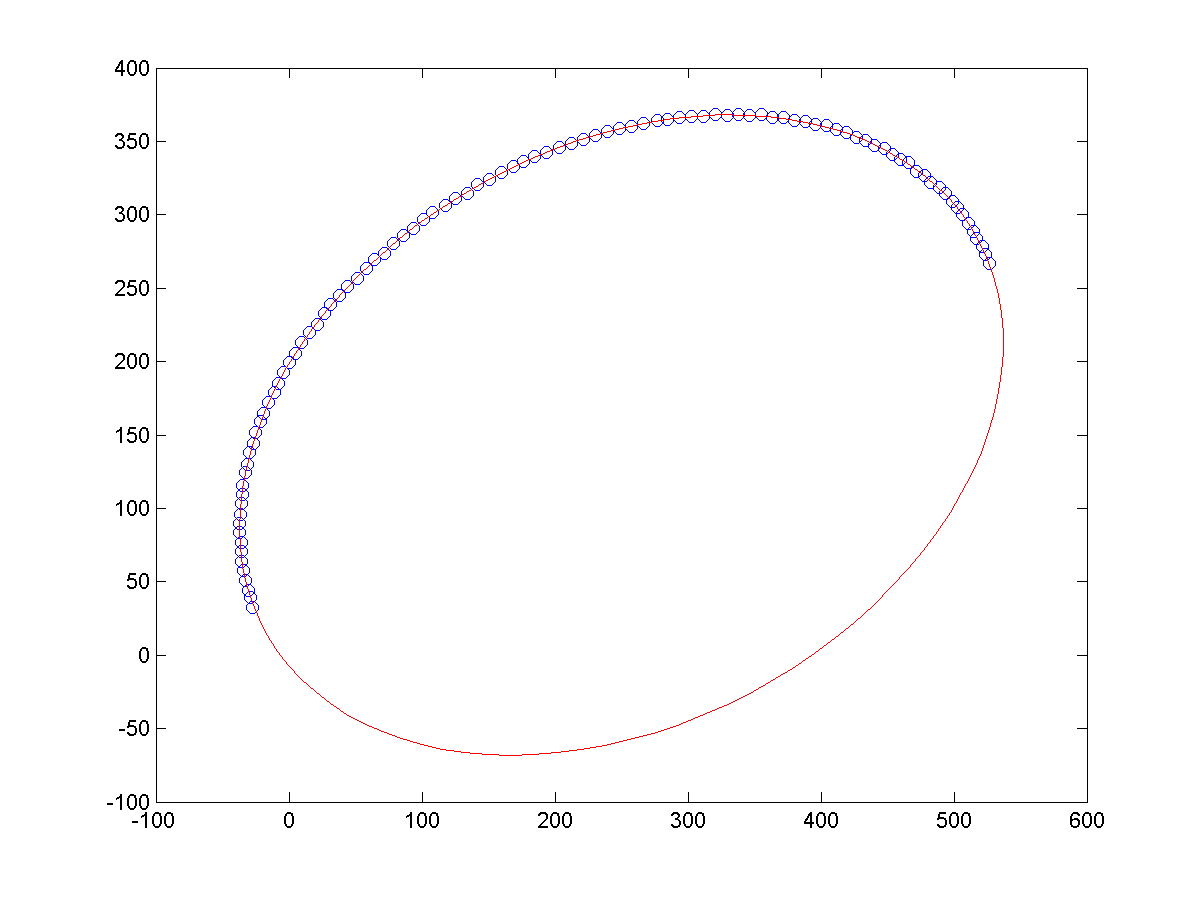
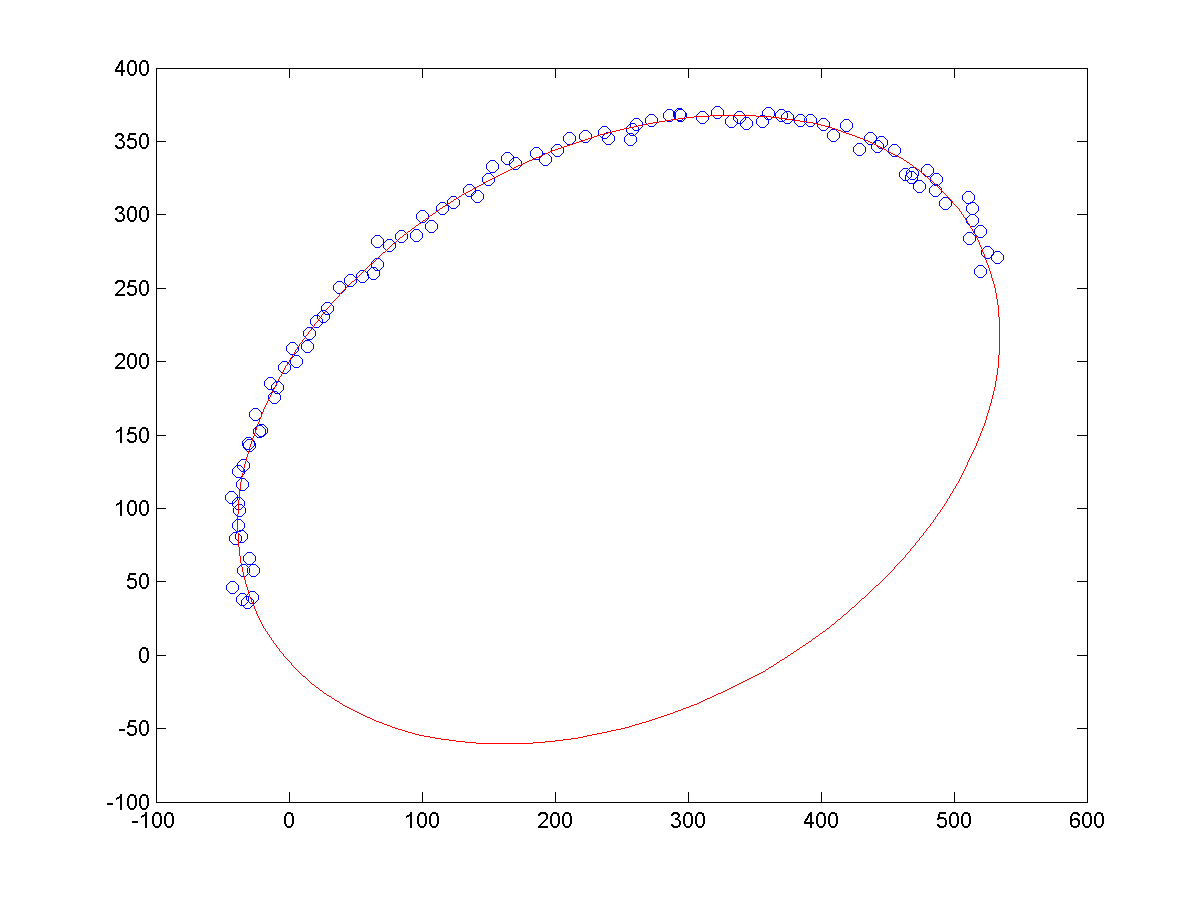
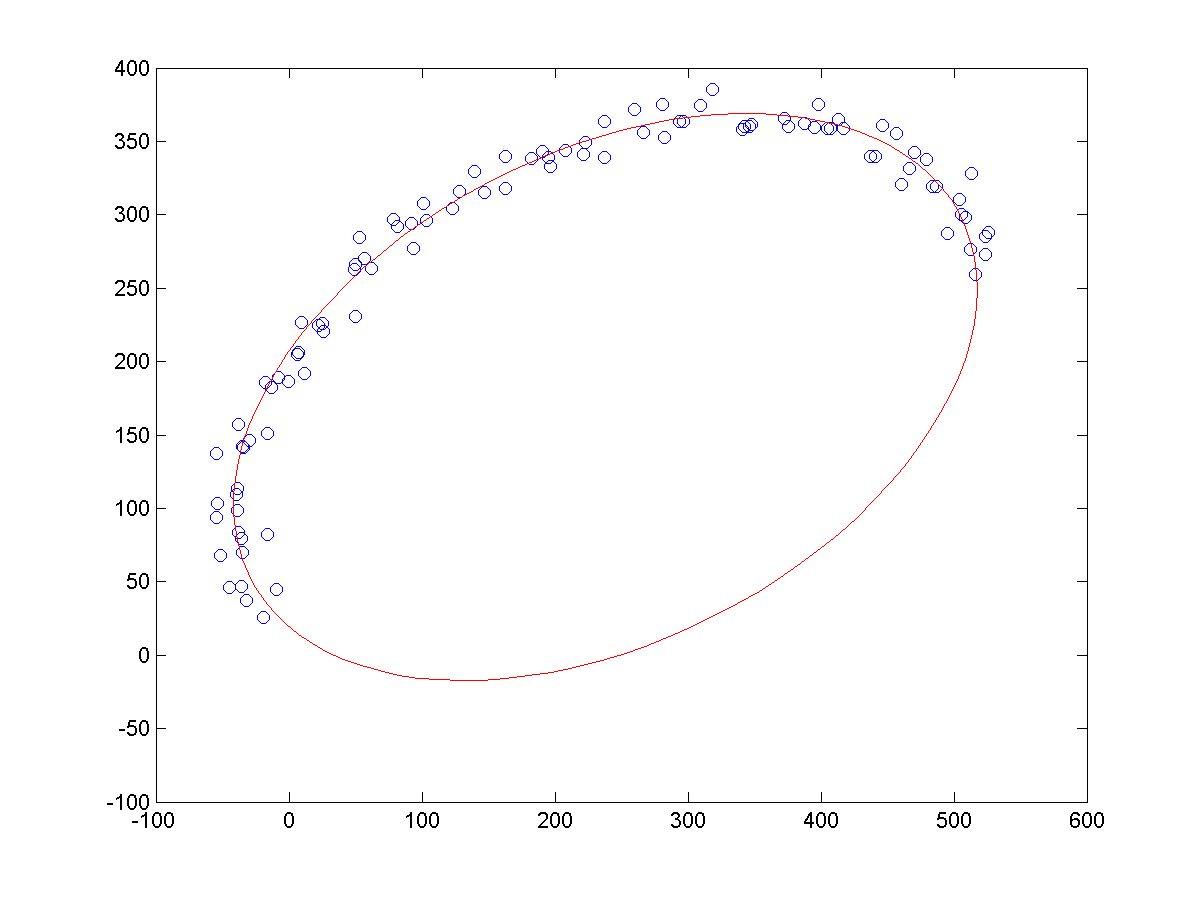
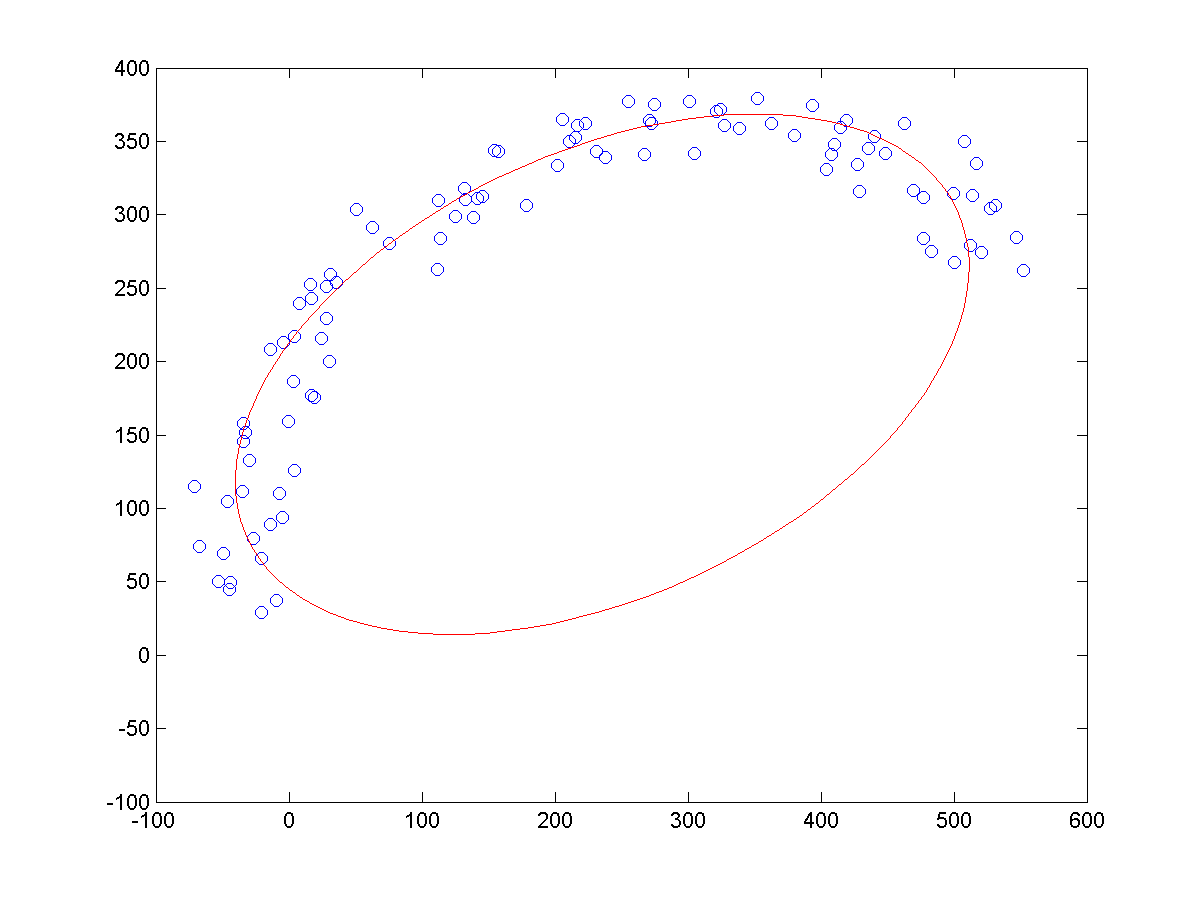

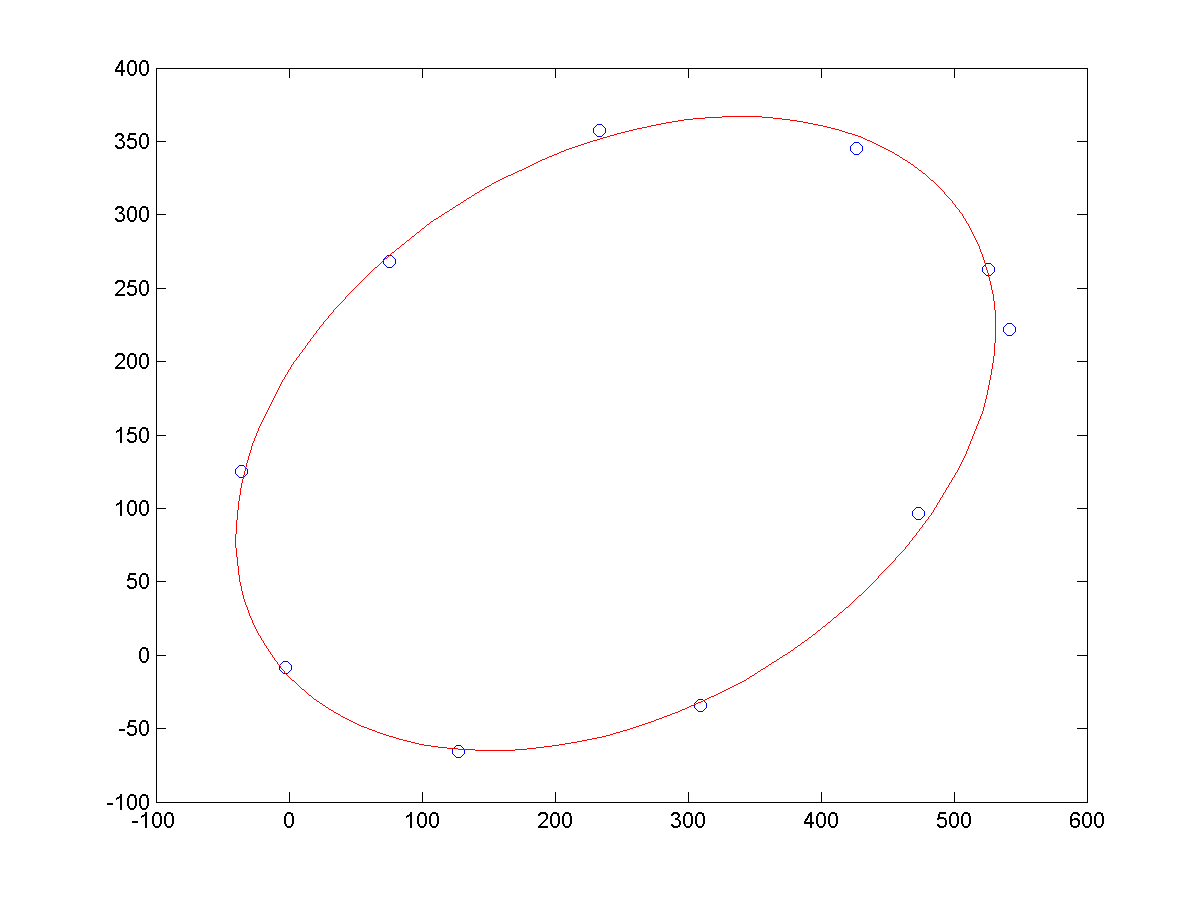
c、少样本点下,拟合结果如下:
源码下载:
地址: FitEllipse
参考文献:
[1]. Andrew W. Fitzgibbon, Maurizio Pilu and Robert B. Fisher. Direct Least Squares Fitting of Ellipses. 1996.
[2]. http://research.microsoft.com/en-us/um/people/awf/ellipse/