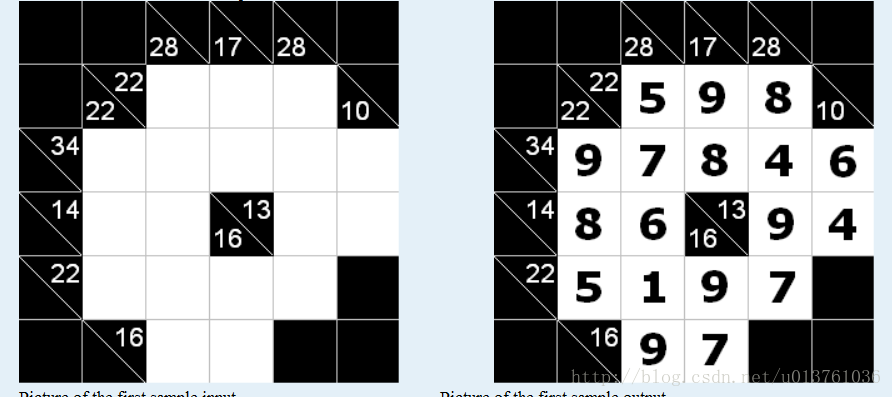
题意:
给你一个N*M的网格,上面有的有一些数字,要求填充数字,满足的规则是这样:
答案不唯一,只要满足和的关系就可以,还有就是只能用1--9之间的数字填充,而且每一行或一列可以重复使用某个数字,观察每个要填充的点我们会发现,其实该点只于他所在的"行和"限制和所在的"列和"限制,我们可以把点分为三类,白色填充,左下半有数,右下半
有数 ,(其他的没用,不用管 ,左下和右上都有数的一定要拆成两个点),只要权衡好这三类点就ok了,那么我们可以直接添加 超级远点s ,超级汇点e ,左下进右上出(也可以反过来);题目要求是1--9 ,最大流可能会产生0所以直接0--8,输出的时候在+1就行.题意既然说是保证有解,那么最大流肯定会满流,最后每个点流多少就输出多少+1就ok;
建图:
(1)s 和所有左下有数的点连 ,流量是左下的数字减去他下面空白行的个数(因为是0--8每个都少了1 ,一共有多少个就少多少个)
(2)所有左下角有数的点和他下面的这一列的空白点相连,流量 8
(3)所有右上角有数的被他所在的这一列空白的连接,记住是被连接,(方向别反了),还有注意一点就是如果该点左下角有数了,那么一定要拆点,不然会冲突,流量是8;
(4)第三步中所有被连接的点在连接e,流量是该点右上角的数 - 这一行的空白格子个数.原因和(1) 一样.
建图后直接一遍最大流,然后根据流量情况就能输出答案了, 题目是 Special Judge ..所以随便跑一遍就行了,还有就是别用DINIC,会超时,就算我把点都离散化了依然超时,我用的是
SAP之前没用过,随便找了个模板改改用的. 当某个点有两个值时一定要拆点.同时可以离散化去优化.
下面是代码,第一个是TLE代码(DINIC),第二个是AC代码(SAP);
// 超时的DINIC
#include<stdio.h>
#include<string.h>
#include<queue>
#define N_node 100 * 100 * 2 + 100
#define N_edge 500000
#define N 100 + 5
#define inf 1000000000
using namespace std;
typedef struct
{
char node[8];
}NODE;
typedef struct
{
int to ,next ,cost;
}STAR;
typedef struct
{
int x ,dep;
}DEP;
NODE map[N][N];
STAR E[N_edge];
DEP xin ,tou;
int list[N_node] ,tot;
int list2[N_node] ,deep[N_node];
int X[N*N*2+100];
void add(int a ,int b ,int c)
{
E[++tot].to = b;
E[tot].cost = c;
E[tot].next = list[a];
list[a] = tot;
E[++tot].to = a;
E[tot].cost = 0;
E[tot].next = list[b];
list[b] = tot;
}
int minn(int x ,int y)
{
return x < y ? x : y;
}
bool BFS_DEEP(int s ,int t ,int n)
{
memset(deep ,255 ,sizeof(deep));
deep[s] = 0;
xin.x = s ,xin.dep = 0;
queue<DEP>q;
q.push(xin);
while(!q.empty())
{
tou = q.front();
q.pop();
for(int k = list[tou.x] ;k ;k = E[k].next)
{
xin.x = E[k].to;
xin.dep = tou.dep + 1;
if(deep[xin.x] != -1 || !E[k].cost)
continue;
deep[xin.x] = xin.dep;
q.push(xin);
}
}
for(int i = 0 ;i <= n ;i ++)
list2[i] = list[i];
return deep[t] != -1;
}
int DFS_FLOW(int s ,int t ,int flow)
{
if(s == t) return flow;
int nowflow = 0;
for(int k = list2[s] ;k ;k = E[k].next)
{
list2[s] = k;
int to = E[k].to;
int c = E[k].cost;
if(deep[to] != deep[s] + 1 || !c)
continue;
int temp = DFS_FLOW(to ,t ,minn(c ,flow - nowflow));
nowflow += temp;
E[k].cost -= temp;
E[k^1].cost += temp;
if(nowflow == flow) break;
}
if(!nowflow) deep[s] = 0;
return nowflow;
}
int DINIC(int s ,int t ,int n)
{
int ans = 0;
while(BFS_DEEP(s ,t ,n))
{
ans += DFS_FLOW(s ,t ,inf);
}
return ans;
}
int main ()
{
int i ,j ,n ,m ,s ,e;
while(~scanf("%d %d" ,&n ,&m))
{
int sum_n = 0;
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
scanf("%s" ,map[i][j].node);
if(map[i][j].node[0] == '.')
{
sum_n ++;
continue;
}
if(map[i][j].node[0] != 'X')
sum_n ++;
if(map[i][j].node[4] != 'X')
sum_n ++;
}
s = 0 ,e = sum_n + 1;
sum_n = 0;
memset(X ,255 ,sizeof(X));
memset(list ,0 ,sizeof(list)) ,tot = 1;
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
if(map[i][j].node[3] == 'X' || map[i][j].node[0] == '.') continue;
char t_str[8];
for(int ii = 0 ;ii <= 7 ;ii ++)
t_str[ii] = map[i][j].node[ii];
int a ,b ,mk = 0;
if(X[(i-1)*m+j] == -1) X[(i-1)*m+j] = ++sum_n;
int now = X[(i-1)*m+j];
if(t_str[0] != 'X')
{
mk = 1;
int temp = (t_str[0]-48)*100+(t_str[1]-48)*10+(t_str[2]-48)*1;
for(int ii = i + 1 ;ii <= n ;ii ++)
{
if(map[ii][j].node[0] != '.')
break;
temp --;
if(X[(ii - 1) * m + j] == -1) X[(ii - 1) * m + j] = ++sum_n;
b = X[(ii - 1) * m + j];
add(now ,b ,8);
}
add(s ,now ,temp);
}
if(t_str[4] != 'X')
{
if(mk) now = ++sum_n;
int temp = (t_str[4]-48)*100+(t_str[5]-48)*10+(t_str[6]-48)*1;
for(int jj = j + 1 ;jj <= m ;jj ++)
{
if(map[i][jj].node[0] != '.')
break;
temp --;
if(X[(i - 1) * m + jj] == -1) X[(i - 1) * m + jj] = ++sum_n;
a = X[(i - 1) * m + jj];
add(a ,now ,8);
}
add(now ,e ,temp);
}
}
DINIC(s ,e ,sum_n + 1);
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
if(j != 1) printf(" ");
if(map[i][j].node[0] != '.')
printf("_");
else
{
int k = list[X[(i - 1) * m + j]];
int c = E[k].cost;
printf("%d" ,8 - c + 1);
}
if(j == m) printf("
");
}
}
return 0;
}
//SAP ac
#include<stdio.h>
#include<string.h>
#include<queue>
#define N 100 + 5
using namespace std;
typedef struct
{
char node[8];
}NODE;
NODE map[N][N];
int X[50000];
//***********************************************
const int MAXN=50000;//点数的最大值
const int MAXM=1000000;//边数的最大值
const int INF=0x3f3f3f3f;
struct Node
{
int from,to,next;
int cap;
}edge[MAXM];
int tol;
int head[MAXN];
int dep[MAXN];
int gap[MAXN];//gap[x]=y :说明残留网络中dep[i]==x的个数为y
int nn;//n是总的点的个数,包括源点和汇点
void init()
{
tol=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int w)
{
edge[tol].from=u;
edge[tol].to=v;
edge[tol].cap=w;
edge[tol].next=head[u];
head[u]=tol++;
edge[tol].from=v;
edge[tol].to=u;
edge[tol].cap=0;
edge[tol].next=head[v];
head[v]=tol++;
}
void BFS(int start,int end)
{
memset(dep,-1,sizeof(dep));
memset(gap,0,sizeof(gap));
gap[0]=1;
int que[MAXN];
int front,rear;
front=rear=0;
dep[end]=0;
que[rear++]=end;
while(front!=rear)
{
int u=que[front++];
if(front==MAXN)front=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(dep[v]!=-1)continue;
que[rear++]=v;
if(rear==MAXN)rear=0;
dep[v]=dep[u]+1;
++gap[dep[v]];
}
}
}
int SAP(int start,int end)
{
int res=0;
BFS(start,end);
int cur[MAXN];
int S[MAXN];
int top=0;
memcpy(cur,head,sizeof(head));
int u=start;
int i;
while(dep[start]<nn)
{
if(u==end)
{
int temp=INF;
int inser;
for(i=0;i<top;i++)
if(temp>edge[S[i]].cap)
{
temp=edge[S[i]].cap;
inser=i;
}
for(i=0;i<top;i++)
{
edge[S[i]].cap-=temp;
edge[S[i]^1].cap+=temp;
}
res+=temp;
top=inser;
u=edge[S[top]].from;
}
if(u!=end&&gap[dep[u]-1]==0)//出现断层,无增广路
break;
for(i=cur[u];i!=-1;i=edge[i].next)
if(edge[i].cap!=0&&dep[u]==dep[edge[i].to]+1)
break;
if(i!=-1)
{
cur[u]=i;
S[top++]=i;
u=edge[i].to;
}
else
{
int min=nn;
for(i=head[u];i!=-1;i=edge[i].next)
{
if(edge[i].cap==0)continue;
if(min>dep[edge[i].to])
{
min=dep[edge[i].to];
cur[u]=i;
}
}
--gap[dep[u]];
dep[u]=min+1;
++gap[dep[u]];
if(u!=start)u=edge[S[--top]].from;
}
}
return res;
}
//**************************************
int main ()
{
int i ,j ,n ,m ,s ,e;
while(~scanf("%d %d" ,&n ,&m))
{
int sum_n = 0;
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
scanf("%s" ,map[i][j].node);
if(map[i][j].node[0] == '.')
{
sum_n ++;
continue;
}
if(map[i][j].node[0] != 'X')
sum_n ++;
if(map[i][j].node[4] != 'X')
sum_n ++;
}
s = 0 ,e = sum_n + 1;
sum_n = 0;
memset(X ,255 ,sizeof(X));
memset(head ,255 ,sizeof(head));
tol = 0;
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
if(map[i][j].node[3] == 'X' || map[i][j].node[0] == '.') continue;
char t_str[8];
for(int ii = 0 ;ii <= 7 ;ii ++)
t_str[ii] = map[i][j].node[ii];
int a ,b ,mk = 0;
if(X[(i-1)*m+j] == -1) X[(i-1)*m+j] = ++sum_n;
int now = X[(i-1)*m+j];
if(t_str[0] != 'X')
{
mk = 1;
int temp = (t_str[0]-48)*100+(t_str[1]-48)*10+(t_str[2]-48)*1;
for(int ii = i + 1 ;ii <= n ;ii ++)
{
if(map[ii][j].node[0] != '.')
break;
temp --;
if(X[(ii - 1) * m + j] == -1) X[(ii - 1) * m + j] = ++sum_n;
b = X[(ii - 1) * m + j];
addedge(now ,b ,8);
}
addedge(s ,now ,temp);
}
if(t_str[4] != 'X')
{
if(mk) now = ++sum_n;
int temp = (t_str[4]-48)*100+(t_str[5]-48)*10+(t_str[6]-48)*1;
for(int jj = j + 1 ;jj <= m ;jj ++)
{
if(map[i][jj].node[0] != '.')
break;
temp --;
if(X[(i - 1) * m + jj] == -1) X[(i - 1) * m + jj] = ++sum_n;
a = X[(i - 1) * m + jj];
addedge(a ,now ,8);
}
addedge(now ,e ,temp);
}
}
nn = sum_n + 1 + 1;
SAP(s ,e);
for(i = 1 ;i <= n ;i ++)
for(j = 1 ;j <= m ;j ++)
{
if(j != 1) printf(" ");
if(map[i][j].node[0] != '.')
printf("_");
else
{
int k = head[X[(i - 1) * m + j]];
int c = edge[k].cap;
printf("%d" ,8 - c + 1);
}
if(j == m) printf("
");
}
}
return 0;
}