There are n integers b1, b2, ..., bn written in a row. For all i from 1 to n, values ai are defined by the crows performing the following procedure:
- The crow sets ai initially 0.
- The crow then adds bi to ai, subtracts bi + 1, adds the bi + 2 number, and so on until the n'th number. Thus, ai = bi - bi + 1 + bi + 2 - bi + 3....
Memory gives you the values a1, a2, ..., an, and he now wants you to find the initial numbers b1, b2, ..., bn written in the row? Can you do it?
- Input
The first line of the input contains a single integer n (2 ≤ n ≤ 100 000) — the number of integers written in the row.
The next line contains n, the i'th of which is ai ( - 109 ≤ ai ≤ 109) — the value of the i'th number.
- Output
Print n integers corresponding to the sequence b1, b2, ..., bn. It's guaranteed that the answer is unique and fits in 32-bit integer type.
- Examples
5
6 -4 8 -2 3
2 4 6 1 3
5
3 -2 -1 5 6
1 -3 4 11 6
- Note
In the first sample test, the crows report the numbers 6, - 4, 8, - 2, and 3 when he starts at indices 1, 2, 3, 4 and 5 respectively. It is easy to check that the sequence 2 4 6 1 3 satisfies the reports. For example, 6 = 2 - 4 + 6 - 1 + 3, and - 4 = 4 - 6 + 1 - 3.
In the second sample test, the sequence 1, - 3, 4, 11, 6 satisfies the reports. For example, 5 = 11 - 6 and 6 = 6.
题意:
存在n个数b1,,b2,...,bn,
a1,a2, ..., an 是通过等式 ai = bi - b(i+1) + b(i+2) - b(i+3)....(±)bn 得到的。
现给你a1,a2,...,an这n个数,问b1, b2, ..., bn是多少?
【分析】
∵ ai = bi - b(i+1) + b(i+2) - b(i+3)....
∴ bi = ai + b(i+1) - b(i+2) +b(i+3)....
又 ∵ b(i+1) = a(i+1) + b(i+2) - b(i+3) +b(i+4)....
∴ bi = ai + [ a(i+1) + b(i+2) - b(i+3) +b(i+4).... ] - b(i+2) +b(i+3)....
= ai + a(i+1)
而且,an = bn
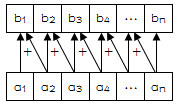
即数组b的第 i 项是数组a的第 i 项和第 i+1 项之和。
【时间复杂度】 O(n)
【代码实现】
1 #include<stdio.h>
2 int main(){
3 int n,a,b,i;
4 while(1){
5 scanf("%d",&n);
6 for(i = 1;i <= n; i++){
7 scanf("%d",&a);
8 if(i>1)
9 printf("%d ",a+b);
10 b = a;
11 }
12 printf("%d",b);
13 }
14 return 0;
15 }