【语言处理与Python】10.4英语句子的语义

基于特征的文法中的合成语义学

组合原则：整体的含义是部分的含义与它们的句法结合方式的函数。

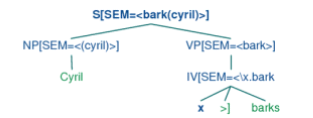
我们的目标是以一种可以与分析过程平滑对接的方式整合语义表达的构建。类似于下面这幅图：

SEM 是语义的意思。

1、根节点的SEM显示了整个句子的语义表示。

2、较低节点的SEM值显示了句子的成分。

3、SEM值要以特殊的方式对待，所以被放在了尖括号里面。

可以这样构造文法：

S[SEM=<?vp(?np)>]-> NP[SEM=?subj]VP[SEM=?vp]
VP[SEM=?v]-> IV[SEM=?v]
NP[SEM=<cyril>]-> 'Cyril'
IV[SEM=<\x.bark(x)>] -> 'barks'

在讲述组合语义规则的细节之前，需要为我们的工具箱添加新的工具，成为λ演算。用于在哦呜们组装一个英文句子的意思表示时，组合一阶逻辑表达式。

λ演算

{w| w∈V&P(w)}

这个集合表明了，所有w的集合，其中w是V（词汇表）的元素且w有属性P。

我们需要添加一些能达到同样效果的东西到一阶逻辑中是非常有用的。我们用λ运算符来做这个工作。

例如：

λw.(V(w) &P(w))

λ是约束运算符，就像一阶逻辑量词。

如果我们有一个开放公式，可以将x与λ进行绑定。

(33)a. (walk(x) &chew_gum(x))
b.λx.(walk(x) &chew_gum(x))
c.\x.(walk(x) &chew_gum(x))

>>>lp =nltk.LogicParser()
>>>e = lp.parse(r'\x.(walk(x) &chew_gum(x))')
>>>e
<LambdaExpression\x.(walk(x) &chew_gum(x))>
>>>e.free()
set([])
>>>print lp.parse(r'\x.(walk(x) &chew_gum(y))')
\x.(walk(x) &chew_gum(y))

λ-抽象：

1、一个开放公式φ有自由变量x

2、x抽象为一个属性表达式λ x.φ，满足φ的x的属性

如果φ是一个开放公式，我们有的时候可以把他当作一元谓词：

(36) \x.(walk(x) &chew_gum(x))(gerald)

他与37要表达的意思是一样的。

(37) (walk(gerald) &chew_gum(gerald))

从36到37的操作叫做β-约简，可以这样用代码来演示：

>>>e = lp.parse(r'\x.(walk(x) &chew_gum(x))(gerald)')
>>>print e
\x.(walk(x) &chew_gum(x))(gerald)
>>>print e.simplify() 
(walk(gerald) &chew_gum(gerald))

主体可以是任何符合文法的表达式，下面是一个有两个λ的例子：

(38) \x.\y.(dog(x) &own(y,x))

同样，在我们的代码中也可以演示：

>>>print lp.parse(r'\x.\y.(dog(x) &own(y,x))(cyril)').simplify()
\y.(dog(cyril) &own(y,cyril))
>>>print lp.parse(r'\x y.(dog(x) &own(y, x))(cyril, angus)').simplify() 
(dog(cyril) &own(angus,cyril))

existsx.P(x)和existsy.P(y)是等价的；它们被称为α-等价，或字母变体。

重新标记绑定的变量的过程被称为α-转换。

当我们在logic 模块中测试VariableBinderExpressions是否相等（即使用==）时，我们其实是测试α-等价：

>>>e1 = lp.parse('exists x.P(x)')
>>>print e1
exists x.P(x)
>>>e2 = e1.alpha_convert(nltk.Variable('z'))
>>>print e2
exists z.P(z)
>>>e1 ==e2
True

量化的NP

如果我们要给出42a的逻辑形式42b，如何才能实现呢？

(42) a. A dog barks.
b.exists x.(dog(x) &bark(x))

1、我们将主语的SEM值作为函数表达式，而不是参数。现在我们寻找实例化?np的方式。使[SEM=<?np(\x.bark(x))>]等价于[SEM=<exists x.(dog(x)&bark(x))>]。

2、我们替代42b中出现的\x.bark(x)为一个谓词变量P，并用λ绑定变量，如（43）中所示。

(43) \P.exists x.(dog(x)&P(x))

3、加上限定词

（45) \Q P.exists x.(Q(x)&P(x))

把Q,P分别被\x.dog(x)，\x.bark(x)应用，得到\P.existsx.(dog(x)&P(x))(\x.bark(x))

经过β-约简得到我们想要的，42b。

及物动词

(46) Angus chases a dog.

我们想要得到的输出语义是：exists x.(dog(x)&chase(angus,x))。我们使用λ-抽象得到这样的结果。

下面是chase a dog的成功的语义表示：

(47) \y.exists x.(dog(x)&chase(y,x))

我们把47作为一个y的属性，可以与43结合，派生出47.

我们可以在47上，进行约简的逆操作：

得到48：

(48) \P.exists x.(dog(x)&P(x))(\z.chase(y,z))

现在，让我们用与NP类型相同的变量X，替换48中的函数表达式。

(49) X(\z.chase(y,z))

我们在49的X变量和主语变量y上的抽象：

(50) \X y.X(\x.chase(y,x))

50应用到43，约简后，与47等效：

>>>lp =nltk.LogicParser()
>>>tvp =lp.parse(r'\X x.X(\y.chase(x,y))')
>>>np= lp.parse(r'(\P.exists x.(dog(x) &P(x)))')
>>>vp= nltk.ApplicationExpression(tvp,np)
>>>print vp
(\X x.X(\y.chase(x,y)))(\P.existsx.(dog(x)&P(x)))
>>>print vp.simplify()
\x.exists z2.(dog(z2) &chase(x,z2))

注意：从独立常量angus转换为\P.P(angus)是类型提升的一个例子。

\P.P(angus)(\x.walk(x))和\x.walk(x)(angus)经过约简都能变为walk(angus)

下面演示了一个稍微复杂的例子：

>>>from nltk import load_parser
>>>parser = load_parser('grammars/book_grammars/simple-sem.fcfg', trace=0)
>>>sentence = 'Angus gives a boneto every dog'
>>>tokens = sentence.split()
>>>trees = parser.nbest_parse(tokens)
>>>for tree in trees:
... print tree.node['SEM']
all z2.(dog(z2) -> exists z1.(bone(z1) &give(angus,z1,z2)))

现在，我们已经看到了英文句子如何转换成逻辑形式；

前面我们看到了在模型中如何检查逻辑形式的真假；

现在，把这两个映射放在一起，我们可以检查一个给定的模型中的英语句子的真值。

下面是一个简单的例子：

>>>v= """
... bertie =>b
... olive =>o
... cyril =>c
... boy=>{b}
... girl =>{o}
... dog=>{c}
... walk=>{o, c}
... see =>{(b,o),(c, b),(o, c)}
... """
>>>val = nltk.parse_valuation(v)
>>>g= nltk.Assignment(val.domain)
>>>m=nltk.Model(val.domain, val)
>>>sent = 'Cyril sees every boy'
>>>grammar_file = 'grammars/book_grammars/simple-sem.fcfg'
>>>results = nltk.batch_evaluate([sent],grammar_file, m,g)[0]
>>>for (syntree, semrel, value) in results:
... print semrep
... print value
exists z3.(ankle(z3) &bite(cyril,z3))
True

再述量词歧义

(52) Every girl chases a dog.

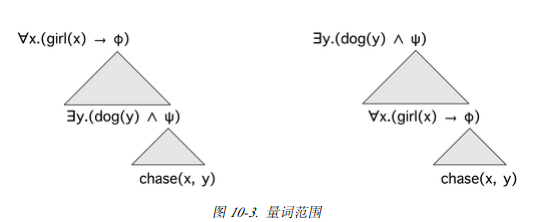
让我们看看，对于52两种不同的读法：

(53)a. all x.(girl(x) -> exists y.(dog(y) &chase(x,y)))
b.exists y.(dog(y) &all x.(girl(x) -> chase(x,y)))

Cooper存储：语义表示不再是一阶逻辑的表达式，而是一个由一个核心语义表示加一个绑定操作符链表组成的配对。

现在假设：已经构建了一个Cooper存储风格的句子52的语义表示，我们把chase(x,y)为核心。给定有关52的两个NP的绑定操作符链表。我们将一个绑定的操作符从链表中挑出来与核心结合。

1、

\P.exists y.(dog(y) &P(y))(\z2.chase(z1,z2))

2、

\P.all x.(girl(x) -> P(x))(\z1.existsx.(dog(x)&chase(z1,x)))

1,2只是其中一种情况，这种绑定操作符和核心的方式组合被称为S-检索。

如果我们允许每种可能的顺序，就得到了每一个可能的范围排序。

接下来的问题是：我们如何建立一个核心+存储表示的组合。前面看到，每个短语和词法规则将有一个SEM特征，现在嵌入特征CORE和STORE。

举一个简单的例子：

Cyril smiles。

smiles的词法规则：

IV[SEM=[CORE=<\x.smile(x)>, STORE=(/)]]-> 'smiles'

Cyril的规则更为复杂：

NP[SEM=[CORE=<@x>,STORE=(<bo(\P.P(cyril),@x)>)]]-> 'Cyril'

谓词bo有两个部分：

1、一个标准表示（类型提升）

2、表达式@x,被称为绑定操作符的地址。@x是原变量，也就是范围在逻辑的独立变量之上的变量。

VP[SEM=?s]-> IV[SEM=?s]
S[SEM=[CORE=<?vp(?subj)>,STORE=(?b1+?b2)]]->
NP[SEM=[CORE=?subj,STORE=?b1]]VP[SEM=[core=?vp,store=?b2]]

我们可以看到，那个句子的分析树：

(S[SEM=[CORE=<smile(z3)>, STORE=(bo(\P.P(cyril),z3))]]
(NP[SEM=[CORE=<z3>, STORE=(bo(\P.P(cyril),z3))]]Cyril)
(VP[SEM=[CORE=<\x.smile(x)>, STORE=()]]
(IV[SEM=[CORE=<\x.smile(x)>, STORE=()]]smiles)))

让我们看看更复杂的例子：

CORE = <chase(z1,z2)>
STORE= (bo(\P.all x.(girl(x) -> P(x)),z1),bo(\P.exists x.(dog(x) &P(x)),z2))

模块nltk.sem.cooper_storage处理将存储形式的语义表示转换成标准逻辑形式的任务。

在下面的例子中，我们构造了一个CooperStore实例，并检查他的STORE和CORE。

>>>from nltk.sem import cooper_storageas cs
>>>sentence = 'every girl chasesa dog'
>>>trees = cs.parse_with_bindops(sentence, grammar='grammars/book_grammars/storage.fcfg')
>>>semrep = trees[0].node['sem']
>>>cs_semrep = cs.CooperStore(semrep)
>>>print cs_semrep.core
chase(z1,z2)
>>>for boin cs_semrep.store:
... print bo
bo(\P.all x.(girl(x) -> P(x)),z1)
bo(\P.existsx.(dog(x) &P(x)),z2)

最后，我们用s_retrieve（）来检查读法：

>>>cs_semrep.s_retrieve(trace=True)
Permutation1
(\P.all x.(girl(x) -> P(x)))(\z1.chase(z1,z2))
(\P.exists x.(dog(x) &P(x)))(\z2.allx.(girl(x) -> chase(x,z2)))
Permutation2
(\P.exists x.(dog(x) &P(x)))(\z2.chase(z1,z2))
(\P.all x.(girl(x) -> P(x)))(\z1.existsx.(dog(x) &chase(z1,x)))
>>>for reading in cs_semrep.readings:
... print reading
exists x.(dog(x)&all z3.(girl(z3) -> chase(z3,x)))
all x.(girl(x) -> exists z4.(dog(z4) &chase(x,z4)))