[NOI2016] 优秀的拆分

题目

点这里看题目。

分析

95 pts 的大暴力，枚举 AA 这样的串并且在起点、终点处记录数量。

话说 95pts 给 (O(n^2)) 相当足了!

目测，我们只能优化统计的过程。注意到对于 AA 串，设 (|A|=l)，那么该串最多只会穿过两个相距 (l) 的点。我们可以枚举一组点，两两相邻 (l)，那么就可以统计穿过相邻点的 AA 串。

具体来说，假如我们枚举 (a,b)，满足 (b=a+l)。那么当我们截取出一组合法的 AA 串、得到了子串 (S') 的时候，就一定会有 (operatorname{LCS}(S'[:a], S'[:b])+operatorname{LCP}(S'[a:], S'[b:])=l+1) 。

因此我们可以找出原串上两个前缀、后缀的 (operatorname{LCS}) 和 (operatorname{LCP})，并考虑此时合法的 AA：

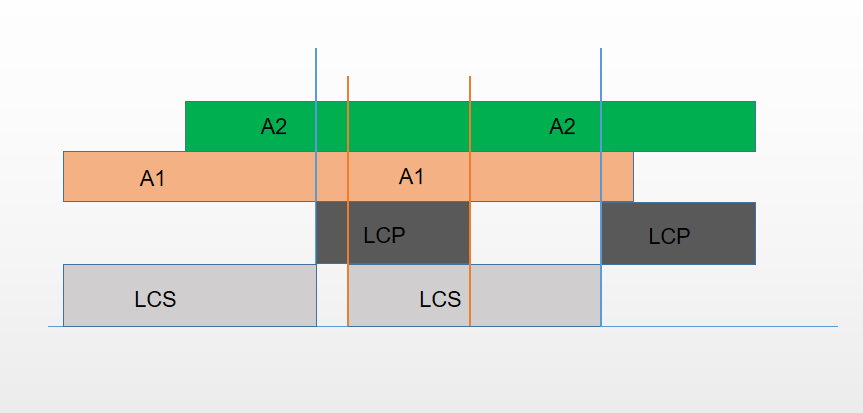
可以发现，经过了 (a,b) 的任意两个 A 的连接点均落在橙线之间，因此此时会被贡献到的起点、终点都必然是一段区间，且可以使用差分实现 (O(1)) 修改。

需要注意的是，为了避免计算跨越其他点的 AA，我们需要限制 (operatorname{LCS}) 和 (operatorname{LCP}) 的长度均不超过 (l) 。

时间复杂度取决于求 (operatorname{LCS}) 和 (operatorname{LCP}) 的时间效率，不过 (O(nlog_2^2n)) 和 (O(nlog_2n)) 都是可以通过的。

小结：

1. 这道题中处理 AA 的方法确实比较巧妙，利用到的是复制的形式带来的相同结构和重复出现的性质。
2. 其实考场上就写 95pts 应该也是完全足够的。

代码

#include <cstdio>
#include <cstring>
using namespace std;

#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )

typedef long long LL;

const int mod = 104857601, BASE = 29;
const int MAXN = 1e5 + 5;

template<typename _T>
void read( _T &x )
{
	x = 0; char s = getchar(); int f = 1;
	while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
	while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ) putchar( '-' ), x = -x;
	if( 9 < x ) write( x / 10 );
	putchar( x % 10 + '0' );
}

template<typename _T>
_T MIN( const _T a, const _T b )
{
	return a < b ? a : b;
}

template<typename _T>
_T MAX( const _T a, const _T b )
{
	return a > b ? a : b;
}

int pref[MAXN], pw[MAXN];

int edCnt[MAXN], bgCnt[MAXN];

char S[MAXN];
int N;

inline int Mul( int x, int v ) { return 1ll * x * v % mod; }
inline int Sub( int x, int v ) { return ( x -= v ) < 0 ? x + mod : x; }
inline int Add( int x, int v ) { return ( x += v ) >= mod ? x - mod : x; }

int Get( const int l, const int r )
{
	return Sub( pref[r], Mul( pref[l - 1], pw[r - l + 1] ) );
}

int LCP( const int a, const int b )
{
	if( S[a] ^ S[b] ) return 0;
	int l = 1, r = MIN( a, b ), mid;
	while( l < r )
	{
		mid = l + r + 1 >> 1;
		if( Get( a - mid + 1, a ) == Get( b - mid + 1, b ) ) l = mid;
		else r = mid - 1;
	}
	return l;
}

int LCS( const int a, const int b )
{
	if( S[a] ^ S[b] ) return 0;
	int l = 1, r = MIN( N - a + 1, N - b + 1 ), mid;
	while( l < r )
	{
		mid = l + r + 1 >> 1;
		if( Get( a, a + mid - 1 ) == Get( b, b + mid - 1 ) ) l = mid;
		else r = mid - 1;
	}
	return l;
}

void Calc( const int L )
{
	for( int i = L, j = L << 1 ; j <= N ; i += L, j += L )
	{
		int lcs = LCS( i, j ), lcp = LCP( i, j );
		lcs = MIN( lcs, L ), lcp = MIN( lcp, L );
		if( lcs + lcp > L )
		{	
			bgCnt[i - lcp + 1] ++, bgCnt[i + lcs - L + 1] --;
			edCnt[j - lcp + L] ++, edCnt[j + lcs - 1 + 1] --;
		}
	}
}

int main()
{
//	freopen( "excellent.in", "r", stdin );
//	freopen( "excellent.out", "w", stdout );
	int T;
	read( T );
	pw[0] = 1;
	for( int i = 1 ; i <= 3e4 ; i ++ )
		pw[i] = Mul( pw[i - 1], BASE );
	while( T -- )
	{
		scanf( "%s", S + 1 );
		N = strlen( S + 1 ), pref[0] = 0;
		rep( i, 1, N )
			pref[i] = Add( Mul( pref[i - 1], BASE ), S[i] - 'a' ),
			edCnt[i] = bgCnt[i] = 0;
		rep( i, 1, N >> 1 ) Calc( i );
		LL ans = 0;
		rep( i, 1, N ) bgCnt[i] += bgCnt[i - 1], edCnt[i] += edCnt[i - 1];
		rep( i, 1, N - 1 ) ans += 1ll * edCnt[i] * bgCnt[i + 1];
		write( ans ), putchar( '
' );
	}
	return 0;
}