本文翻译了Image Processing Toolbox User’s Guide(R2012b)的6-6(P222)至6-21(P237)部分。
裁剪图像(Cropping an Image)
注意 您也可以使用交互式图像工具Image Tool裁剪图像——请看“使用图像裁剪工具裁剪图像”。
为了从图像中提取出一部分矩形区域,可使用imcrop函数。使用imcrop,您可以使用鼠标交互来确定裁剪区域,也可以通过程序确定裁剪区域的大小和位置。
这个例子说明了交互式用法。示例读入了一幅图像到MATLAB工作空间里,然后以这幅图像为参数调用imcrop函数。imcrop会在一个图形窗口中显示这幅图像,并等待您在图像上画出裁剪矩形。当您的鼠标移动到图像之上时,鼠标指针形状会变为十字线┼。点击并拖拽指针以确定裁剪区域的大小和位置。您可以使用鼠标移动和调整裁剪矩形的尺寸。当您对裁剪矩形满意时,双击以完成裁剪操作,也可以在裁剪矩形内部右击并在右键菜单中选择Crop Image。imcrop返回裁剪后的图像在J中。
I = imread('circuit.tif');
J = imcrop(I);

您也可以在调用imcrop时指定裁剪矩形的大小和位置作为参数。通过一个4元素的位置向量[xmin ymin width height]指定裁剪矩形。
在这个例子中,您调用imcrop并指定了要裁剪的图像I和裁剪矩形。imcrop返回裁剪后的图像保存在J中。
I = imread('circuit.tif');
J = imcrop(I,[60 40 100 90]);
进行通用二维空间变换(Perform General 2-D Spatial Transformations)
空间变换步骤(Spatial Transformation Procedure)
进行通用二维空间变换共有三步:
1 定义空间变换的参数。请看“定义变换数据”以获取更多信息。
2 创建名为TFORM的变换结构体,定义了您想要进行的空间变换的类型。
TFORM是一个MATLAB结构体,它包含了执行变换所需的全部参数。您可以在TFORM中定义很多种空间变换,包括仿射变换,例如平移、缩放、旋转、扭曲,透视变换和自定义变换。获取更多信息,请参阅“Control Point Registration”。(您也可以使用cp2tform函数创建TFORM。)
3 执行变换。为完成变换,您需要将要变换的图像和TFORM结构体传送给imtransform函数。
下面的图表阐释了这个流程。

通用二维空间变换流程概观
使用maketform和imtransform变换图像(Translate Image Using maketform and imtransform)
这个例子说明了如何使用maketform和imtransform函数对一幅图像进行二维空间变换。例中进行了名为平移的简单仿射变换。在平移变换中,您通过在x坐标和y坐标上加上指定数值使图像在空间坐标中移动。示例按照如下步骤阐明:
第1步:导入要变换的图像(Step 1:Import the Image to Be Transformed)
将要变换的图像导入MATLAB工作空间中。本例使用checkerboard函数创建了一幅棋盘图像。checkerboard默认创建一幅80×80像素的图像。
cb = checkerboard;
imshow(cb)

原始图像
第2步:定义空间变换(Step 2:Define the Spatial Transformation)
您必须定义您想要执行的空间变换。对于很多种二维空间变换,例如仿射变换,您可以使用一个3×3的变换矩阵来指定变换。您也可以使用输入和输出图像中的点集来确定变换,让maketform自动创建变换矩阵。欲知更多,请参阅“Defining the Transformation Data”。
本例使用下列的变换矩阵来定义一个平移空间变换。
xform = [ 1 0 0
0 1 0
40 40 1 ];
此矩阵中,xform(3,1)指定了图像在水平方向上移动的像素距离,xform(3,2)指定了图像在垂直方向上移动的像素距离。
第3步:创建TFORM结构体(Create the TFORM Structure)
您需要使用maketform函数创建一个TFORM结构体。您要指定欲进行的变换的类型和已创建的定义变换的变换矩阵(或点集)作为函数的参数。更多信息请参阅“Creating TFORM Structures”。
本例调用maketform,指定’affine’作为变换类型,因为平移是仿射变换的一种,而xform是在第2步中创建的变换矩阵。
tform_translate = maketform('affine',xform);
第4步:执行变换(Step 4:Perform the Transformation)
执行变换需调用imtransform函数,并指定您要变换的图像和存储了所需变换参数的TFORM结构体。更多信息请看“Performing the Spatial Transformation”。
下面的例子将第1步中创建的棋盘图像和第3步中创建的TFORM结构体传递给imtransform函数。imtransform返回变换后的图像。
[cb_trans xdata ydata] = imtransform(cb, tform_translate);
例中包含两个可选的输出参数:xdata和ydata。这些参数返回输出图像在输出坐标系下的位置。xdata包含输出图像角上像素点的x坐标,ydata包含这些像素点的y坐标。
注意 这章在表达像素位置时使用了空间坐标系。在空间坐标系中,x和y坐标确定了像素的中心。想要了解空间坐标系和像素坐标系间的区别,请看“Expressing Image Locations”。
下图生动地展示了这个变换。按照惯例,输入空间的坐标轴标注为u和v,输出空间的坐标轴标注为x和y。在图中,注意imtransform是怎样改动输入图像中定义像素位置的空间坐标的值的。在(1,1)处的像素现在位于(41,41)。(在棋盘图像中,每一个黑色、白色和灰色方块是10像素高和10像素宽的。)

输入图像被变换
像素值和像素位置。上图展示了imtransform是怎样改变输入空间和输出空间中的像素位置的。输入图像中位于(1,1)的像素现在在输出图像中位于(41,41)。注意,不管怎样,那个像素的值并没有改变。像素点(1,1)在输入图像中是黑色的,输出图像中的像素点(41,41)也是黑色的。
imtransform通过将新位置映射回输入图像中的坐标位置(反向映射)来确定输出图像中像素的值。在平移中,因为输出图像的大小和方向与输入图像相同,确定新位置像素值是一个一对一的映射。对于其他类型的变换,例如缩放或旋转,imtransform需要在输入图像中插值以计算输出图像中的像素值。查看imtransform以获取关于支持的插值方法的信息。
第5步:查看输出图像(Step 5:View the Output Image)
在执行完变换之后,您或许想要查看变换后的图像。这个示例使用了imshow函数来显示变换后的图像。
figure, imshow(cb_trans)

变换后图像
理解变换后图像的坐标。当查看变换后的图像,特别是平移变换时,可能会有变换没有效果的感觉。变换后的图像看起来和原来的图像完全一样。然而,如果您检查imtransform返回的xdata和ydata的值,您可以看到空间坐标已经改变了。输入图像左上角的坐标从(1,1)变为(41,41),输入图像右下角的坐标由(80,80)变为了(120,120)。每一个的值都被加上了40,就像所期望的那样。
xdata =
41 120
ydata =
41 120
视觉上看起来没有改变的原因是imtransform调整了输出图像使其正好包含整个变换后的图像而不是整个输出坐标空间。为了看到相对于原图像的变换效果,您可以使用几个可选的输入参数以指定输出图像的大小和输出图像中要包含多少输出空间。
示例使用了三个可选输入参数中的两个,XData和YData,以指定输出坐标空间中有多少要包含在输出图像里。例中设置了XData和YData以包含原图像的原点,而且足够大以包含整个变换后的图像。
注意 现在输出图像中所有在输入图像中没有对应位置的像素点都是黑色的。imtransform将一个叫fill的值赋给这些像素。这个例子使用了默认的填充值,但您可以指定一个不同的值——详见“Specifying Fill Values”。
cb_trans2 = imtransform(cb, tform_translate, ...
'XData', [1 (size(cb, 2) + xform(3, 1))], ...
'YData', [1 (size(cb, 1) + xform(3, 2))]);
figure, imshow(cb_trans2)

查看变换后的图像与原始坐标空间的关系
定义变换数据(Defining the Transformation Data)
在您执行空间变换之前,您一定要首先定义变换的参数。下面的几节里叙述了两种定义空间变换的方法。
不管使用哪一种方法,您需要将结果传递给maketform函数以创建imtransform需要的TFORM结构体。
使用变换矩阵(Using a Transformation Matrix)
maketform函数可以接受不同大小的变换矩阵以进行N维变换。因为imtransform只进行二维变换,您可以只指定3×3变换矩阵。
例如,您可以使用一个3×3的矩阵来指定任何仿射变换。对于仿射变换,最后一列必须包含0 0 1([zeros(N, 1); 1])。您可以指定一个3×2的矩阵,这样的话,imtransform会自动加上第三列。
下表列出了您使用imtransform可以执行的仿射变换,并列出了定义它们的变换矩阵。您可以组合多重仿射变换为一个矩阵。
| 仿射变换 | 示例 | 变换矩阵 | |
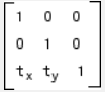
| 平移 |
|
| tx指定沿x轴方向的位移 ty指定沿y轴方向的位移 |
| 比例 |
|
| sx指定沿x轴方向的比例系数 sy指定沿y轴方向的比例系数 |
| 错切 |
|
| shx指定沿x轴方向的错切系数 shy指定沿y轴方向的错切系数 |
| 旋转 |
|
| q指定旋转的角度 |
使用点集(Using Sets of Points)
除了指定变换矩阵,您也可以使用点集来确定变换,而让maketform推断出变换矩阵。
对于仿射变换来说,您必须在输入图像和输出图像中挑选出三个不共线的点。(这些点形成一个三角形。)对于投影变换,您必须选取四个点。(这些点形成一个四边形。)
这个例子在输入图像中选取了三个点,在“Translate Image Using maketform and imtransform”里经过变换的输出图像中选取了三个点。例中将这些点传递给maketform,让maketform推断出变换矩阵。这三个点标记了输入图像中一个棋盘方块和输出图像中同一个方块的三个角。
inpts = [11 11; 21 11; 21 21];
outpts = [51 51; 61 51; 61 61];
tform2 = maketform('affine', inpts, outpts);
创建TFORM结构体(Creating TFORM Structures)
定义完变换数据(“Defining the Transformation Data”)之后,您必须创面一个TFORM结构体以确定空间变换。您要使用maketform函数来创建TFORM结构体。您将TFORM结构体传递给imtransform以执行变换。(您也可以通过cp2tform函数创建TFORM。)
示例创建了指定变换所需参数的TFORM结构体。
tform_translate = maketform('affine', xform);
要创建TFORM,您必须指定欲执行的变换类型并传递进变换数据。例中指定了’affine’作为变换类型,因为这是一个仿射变换,但是maketform也支持投影变换。另外,通过使用custom和composite选项,您可以指定一个几乎没有限制的空间变换类型用于imtransform。下表列出了maketform支持的变换类型。
| 变换类型 | 描述 |
| ‘affine’ 仿射变换 | 包括平移、旋转、比例和错切。变换后,直线仍是直线,平行线保持平行,但矩形有可能变为平行四边形。 |
| ‘projective’ 透视变换 | 变换后,直线仍是直线,但平行线变成汇聚指向灭点。(灭点可以在图像内或图像外——甚至在无穷远点。) |
| ‘box’ | 仿射变换的特例,每一维独立进行平移和比例操作。 |
| ‘custom’ | 用户自定义变换,提供被imtransform调用的正映射和反映射函数。 |
| ‘composite’ | 两种或更多种变换的合成。 |
执行空间变换(Performing the Spatial Transformation)
一旦你在TFORM里指定了变换,您就可以通过调用imtransform来执行变换。imtransform函数在输入图像的坐标上执行指定的变换并生成输出图像。
变换示例中调用了imtransform以执行变换,将要变换的图像和TFORM结构体传递给了它。imtransform返回变换后的图像。
cb_trans = imtransform(cb, tform_translate);
imtransform支持几个可选输入参数,您可以通过它们来控制变换的几个方面,例如输出图像的大小和使用的填充值。要看使用XData和YData输入参数的例子,请看“Register Image Using XData and YData”。更多关于填充值的信息见“Specifying Fill Values”。
指定填充值(Specifying Fill Values)
当执行变换时,输出图像中时常有像素不是原始输入图像的一部分。这些像素必须被赋予一些值,叫做填充值。默认情况下,imtransform将这些像素设为0,显示出来是黑色的。在imtransform中使用FillValues参数,您可以指定一个其它的颜色。
灰度图。如果要变换的图像是灰度图,您必须指定一个标量值以确定灰度的明暗。
例如,在“第5步:查看输出图像”中,示例显示了相对于原始坐标空间的变换后的棋盘图像,您可以指定灰色方块颜色的值作为填充值,而不是默认的黑色。
cb_fill = imtransform(cb, tform_translate, ...
'XData', [1 (size(cb, 2) + xform(3, 1))], ...
'YData', [1 (size(cb, 1) + xform(3, 2))], ...
'FillValues', .7);
figure, imshow(cb_fill)

用灰色填充值的变换后图像
彩色图像。 如果要变换的图像是彩色图像,您可以使用标量值或者1×3向量。如果您指定标量,imtransform对彩色图像的每一个色彩平面使用其对应的明暗值。如果您指定一个1×3向量,imtransform将其解释为RGB颜色值。
例如,这段代码变换一幅彩色图像,指定了一个彩色值作为填充值。例子指定了一种淡绿色的颜色值作为填充值。
rgb = imread('onion.png');
xform = [ 1 0 0
0 1 0
40 40 1 ];
tform_translate = maketform('affine', xform);
cb_rgb = imtransform(rgb, tform_translate, ...
'XData', [1 (size(rgb, 2) + xform(3, 1))], ...
'YData', [1 (size(rgb, 1) + xform(3, 2))], ...
'FillValues', [187; 192; 57]);
figure, imshow(cb_rgb)

使用彩色填充值的变换后彩色图像
如果您在变换多幅彩色图像,您可以为每张彩色图像指定不同的填充值。例如,如果您想转换一组10幅图像,一个大小为200×200×3×10的4维数组,您有几种方案。您可以指定一个标量值,对每一幅图像使用一个灰度级填充值。您也可以用一个1×3的向量为这一组所有的彩色图像指定一个彩色数值。为每一幅彩色图像指定不同的颜色填充值,要指定一个3×10的数组来包含这些颜色值。
进行N维空间变换(Performing N-Dimensional Spatial Transformations)
以下这些函数,当组合使用时,为定义和使用2维、N维和混合维的空间变换提供了丰富的选项。
- maketform
- fliptform
- tformfwd
- tforminv
- tindbounds
- makeresampler
- tformarray
- imtransform
imtransform,findbounds和tformarray函数内部使用了tformfwd和tforminv函数来压缩决定输出图像或数组的范围和将输出像素或数组位置映射回输入位置的正向变换。您可以通过在点和直线上应用tformfwd和tforminv并将结果画出来探索变换的几何效应。它们支持对图像和逐点数据进行一致性处理。
接下来的例子,“Performing the Spatial Transformation”,使用了带标准插值方法的makeresampler函数。您也可以使用它来获取特殊效果或进行自定义处理。例如,您可以指定您自己的可分离的滤波或插值核心,用MATLAB的interp2和interp3函数构造一个自定义的重采样,甚至可以实施先进的抗混叠技术。
而且,正如已经提过的,您可以使用tformarray进行任意维的数组变换。数组甚至不需要有相同的维数。输出可能有比输入更高或者更低的维数。
例如,如果您在2维平面上对3维数据进行采样,输入数组可能会有更低的维数。输出的维数可能会更高,例如,如果您组合多重2维变换成为一个单一的2维至3维的操作。
I = checkerboard(20, 1, 1);
figure; imshow(I)
T = maketform('projective', [1 1; 41 1; 41 41; 1 41], ...
[5 5; 40 5; 35 30; -10 30]);
R = makeresampler('cubic', 'circular');
K = imtransform(I, T, R, 'Size', [100 100], 'XYScale', 1);
figure, imshow(K)


原始图像 变换后图像
imtransform的函数选项让您可以控制变换的很多方面。例如,注意变换后的图像似乎包含了原始图像的多重复制。这是通过使用’Size’选项完成的,使得输出图像比输入图像更大,然后指定填充方法为通过重复循环像素的模式来扩展输入图像。图像处理工具箱图像变换演示提供了使用imtransform函数的更多例子,还有进行不同类型空间变换的相关函数。
备注
本人尽量保证翻译的准确性,但毕竟水平有限,有些地方仅凭个人感觉会意而述。如有疑惑,可参阅英文原版。
我还做了这一部分的ppt演示文档,已上传百度文库,可点此查看。