0 源代码仓库
https://github.com/Cpaulyz/BigDataAnalysis/tree/master/Assignment8
transE.py训练程序graph.py绘制损失函数折线test.py验证测试集
1 目的
知识图谱补全是从已知的知识图谱中提取出三元组(h,r,t),为实体和关系进行建模,通过训练出的模型进行链接预测,以达成知识图谱补全的目标。
本文实验采用了FB15K-237数据集,分为训练集和测试集。利用训练集进行transE建模,通过训练为每个实体和关系建立起向量映射,并在测试集中计算MeanRank和Hit10指标进行结果检验。
2 数据集
使用FB15K-237数据集
分为以下四个文件
-
entity2id.txt
实体和id对
-
relation2id.txt
关系和id对

-
train.txt
训练集三元组(实体,实体,关系)
-
test.txt
测试集三元组(实体,实体,关系)
3 方法
3.1 TransE
3.1.1 原理
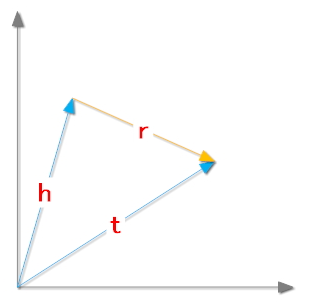
TransE将起始实体,关系,指向实体映射成同一空间的向量,如果(head,relation,tail)存在,那么h+r≈t

目标函数为:
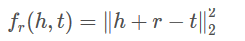
3.1.2 算法

(1)初始化
根据维度,为每个实体和关系初始化向量,并归一化
def emb_initialize(self):
relation_dict = {}
entity_dict = {}
for relation in self.relation:
r_emb_temp = np.random.uniform(-6 / math.sqrt(self.embedding_dim),
6 / math.sqrt(self.embedding_dim),
self.embedding_dim)
relation_dict[relation] = r_emb_temp / np.linalg.norm(r_emb_temp, ord=2)
for entity in self.entity:
e_emb_temp = np.random.uniform(-6 / math.sqrt(self.embedding_dim),
6 / math.sqrt(self.embedding_dim),
self.embedding_dim)
entity_dict[entity] = e_emb_temp / np.linalg.norm(e_emb_temp, ord=2)
(2)选取batch
设置nbatches为batch数目,batch_size = len(self.triple_list) // nbatches
从训练集中随机选择batch_size个三元组,并随机构成一个错误的三元组S',进行更新
def train(self, epochs):
nbatches = 400
batch_size = len(self.triple_list) // nbatches
print("batch size: ", batch_size)
for epoch in range(epochs):
start = time.time()
self.loss = 0
# Sbatch:list
Sbatch = random.sample(self.triple_list, batch_size)
Tbatch = []
for triple in Sbatch:
corrupted_triple = self.Corrupt(triple)
if (triple, corrupted_triple) not in Tbatch:
Tbatch.append((triple, corrupted_triple))
self.update_embeddings(Tbatch)
(3)梯度下降
定义距离d(x,y)来表示两个向量之间的距离,一般情况下,我们会取L1,或者L2 normal。
在这里,我们需要定义一个距离,对于正确的三元组(h,r,t),距离d(h+r,t)越小越好;对于错误的三元组(h',r,t'),距离d(h'+r,t')越小越好。
之后,使用梯度下降进行更新
3.1.3 结果
选择迭代次数2000次,向量维度50,学习率0.01进行训练
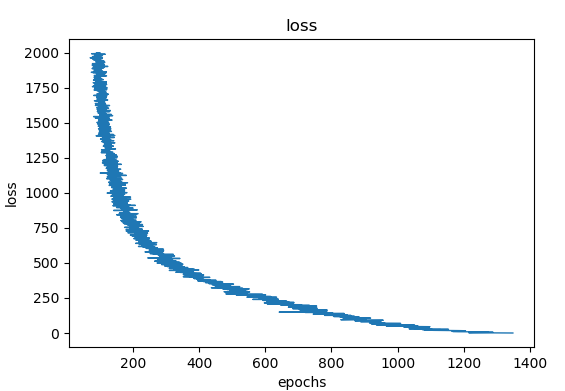
损失函数变化如下
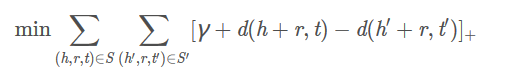
结果存储在entity_50dim和relation_50dim中
3.2 链接预测
通过transE建模后,我们得到了每个实体和关系的嵌入向量,利用嵌入向量,我们可以进行知识图谱的链接预测
将三元组(head,relation,tail)记为(h,r,t)
链接预测分为三类
- 头实体预测:(?,r,t)
- 关系预测:(h,?,t)
- 尾实体预测:(h,r,?)
但原理很简单,利用向量的可加性即可实现。以(h,r,?)的预测为例:
假设t'=h+r,则在所有的实体中选择与t'距离最近的向量,即为t的的预测值
4 指标
4.1 Mean rank
对于测试集的每个三元组,以预测tail实体为例,我们将(h,r,t)中的t用知识图谱中的每个实体来代替,然后通过distance(h, r, t)函数来计算距离,这样我们可以得到一系列的距离,之后按照升序将这些分数排列。
distance(h, r, t)函数值是越小越好,那么在上个排列中,排的越前越好。
现在重点来了,我们去看每个三元组中正确答案也就是真实的t到底能在上述序列中排多少位,比如说t1排100,t2排200,t3排60.......,之后对这些排名求平均,mean rank就得到了。
4.2 Hit@10
还是按照上述进行函数值排列,然后去看每个三元组正确答案是否排在序列的前十,如果在的话就计数+1
最终 排在前十的个数/总个数 就是Hit@10
4.3 代码实现
def distance(h, r, t):
h = np.array(h)
r = np.array(r)
t = np.array(t)
s = h + r - t
return np.linalg.norm(s)
def mean_rank(entity_set, triple_list):
triple_batch = random.sample(triple_list, 100)
mean = 0
hit10 = 0
hit3 = 0
for triple in triple_batch:
dlist = []
h = triple[0]
t = triple[1]
r = triple[2]
dlist.append((t, distance(entityId2vec[h], relationId2vec[r], entityId2vec[t])))
for t_ in entity_set:
if t_ != t:
dlist.append((t_, distance(entityId2vec[h], relationId2vec[r], entityId2vec[t_])))
dlist = sorted(dlist, key=lambda val: val[1])
for index in range(len(dlist)):
if dlist[index][0] == t:
mean += index + 1
if index < 3:
hit3 += 1
if index <10:
hit10 += 1
print(index)
break
print("mean rank:", mean / len(triple_batch))
print("hit@3:", hit3 / len(triple_batch))
print("hit@10:", hit10 / len(triple_batch))
5 结论
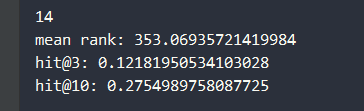
经过transE建模后,在测试集的13584个实体,961个关系的 59071个三元组中,测试结果如下:
mean rank: 353.06935721419984
hit@3: 0.12181950534103028
hit@10: 0.2754989758087725
一方面可以看出训练后的结果是有效的,但不是十分优秀,可能与transE模型的局限性有关,transE只能处理一对一的关系,不适合一对多/多对一关系。