【ybtoj】【强连通分量】软件安装

题意

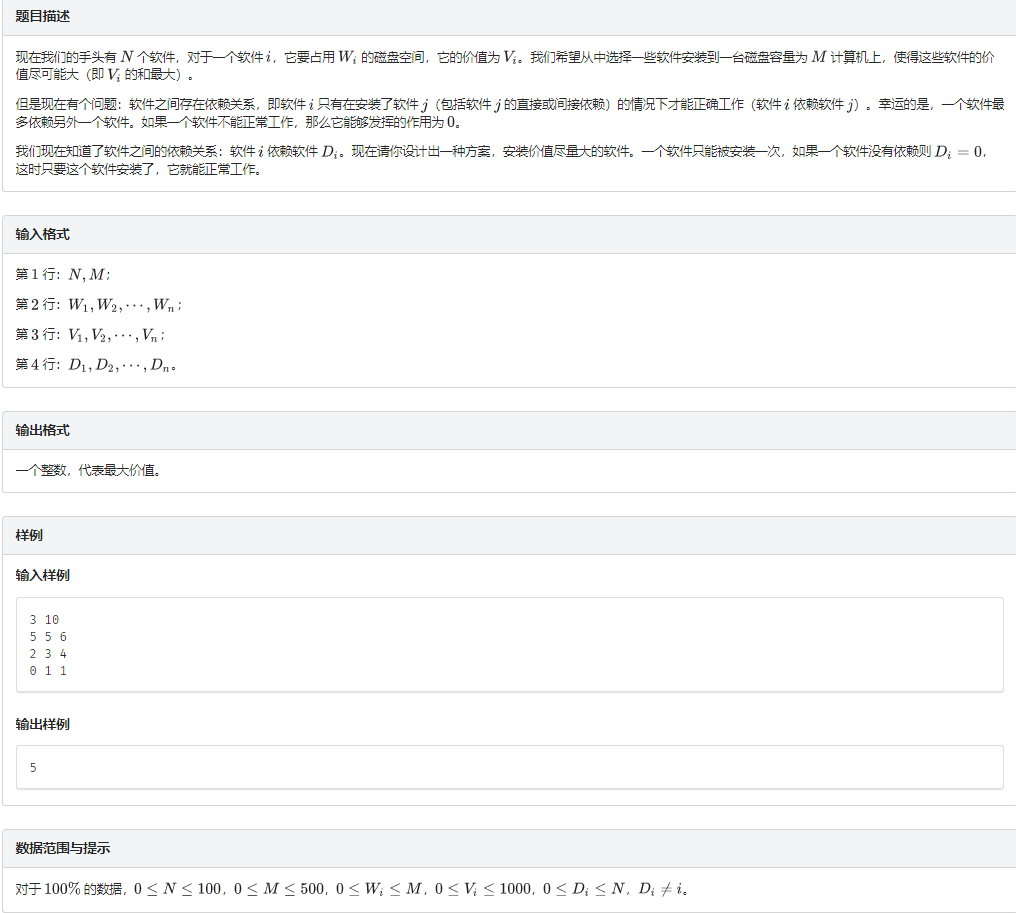
题解

这在洛谷上是一道紫题...不枉我费了半个上午
首先可以想到，一个环里的点，要选择的话一定一起选，所以先想到缩点形成一个DAG
考虑如何建边，注意到题目关键：一个软件最多依赖另外一个软件，那么从被依赖想依赖建边，形成的还是一棵树
问题就转化成了：在一个树上每个点都有重量和价值，你有一个总空间为(m)的背包，选每个点必须选它的父亲，问最多能选出多大价值？
于是乎就是树上背包了
想一下那道经典树形背包：选课，唯一的区别就是那道题每个点的权值和重量都是1
(dp)状态就是(dp[i][j])表示以(i)为根的子树内选大小为(j)的空间所获得最大的价值
但是这道题要注意一些细节：

• 树形dp时候要先初始化再转移
• 转移的时候要保证(j>=sumw[i]),即保证当前的根节点一定能选，否则后面的转移都不成立了（因为是从下往上回溯的时候转移(dp))

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 105,M = 550;
int n,m,head[M],head2[M],ecnt=-1,dfn[N],tim,vist[N],stk[N],tp,ru[N];
int col[N],cnt,siz[N],maxn,low[N],w[N],val[N];
int sumw[N],sumv[N],dp[N][5050];
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
struct edge
{
	int nxt,to;
}a[M],a2[M];
void add(int x,int y)
{
	a[++ecnt]=(edge){head[x],y};
	head[x]=ecnt;
}
void add2(int x,int y)
{
	a2[++ecnt]=(edge){head2[x],y};
	head2[x]=ecnt;
}
void dfs(int u)
{	
	for(int i=m;i>=sumw[u];i--) dp[u][i]=max(dp[u][i],dp[u][i-sumw[u]]+sumv[u]); 
	for(int i=head2[u];~i;i=a2[i].nxt)
	{
		int v=a2[i].to;
		dfs(v);
		for(int j=m;j>=sumw[u];j--)
			for(int k=j;k>=sumw[u];k--)
				if(j-k>=sumw[v]) 
				{
					dp[u][j]=max(dp[u][j],dp[v][j-k]+dp[u][k]);
					//printf("dp[%d][%d]=%d
",u,j,dp[u][j]);
				}
	}

		
}
void tarjan(int u)
{
	dfn[u]=++tim;stk[++tp]=u;low[u]=tim;vist[u]=1;
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(!dfn[v]) 
		{
			tarjan(v);
			low[u]=min(low[v],low[u]);
		}
		else if(vist[v]) low[u]=min(low[v],low[u]);
	}
	if(low[u]==dfn[u])
	{
		++cnt;
		while(stk[tp]!=u)
		{
			col[stk[tp]]=cnt;
			siz[cnt]++;
			sumw[cnt]+=w[stk[tp]],sumv[cnt]+=val[stk[tp]];
			vist[stk[tp]]=0;
			tp--;
		}
		col[u]=cnt,siz[cnt]++,vist[u]=0,tp--;
		sumw[cnt]+=w[u],sumv[cnt]+=val[u];
	}
}
int main()
{
	memset(head,-1,sizeof(head));
	memset(head2,-1,sizeof(head2));
	n=read(),m=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=1;i<=n;i++) val[i]=read();
	for(int i=1,d;i<=n;i++) 
	{
		d=read();
		if(d) add(d,i);
	}
	for(int i=1;i<=n;i++)	
		if(!dfn[i]) tarjan(i);
	ecnt=-1;
	for (int x = 1; x <= n; x++) {
        for (int y = head[x]; ~y; y = a[y].nxt) {
            int v = a[y].to;
            if (col[x] != col[v])
                add2(col[x], col[v]), ru[col[v]]++;
        }
    }
//    for(int i=1;i<=cnt;i++)
//    {
//    	printf("sumw[%d]=%d,sumv[%d]=%d
",i,sumw[i],i,sumv[i]);
//    }
    for(int i=1;i<=cnt;i++) 
    	if(!ru[i]) add2(0,i);
    dfs(0);
    printf("%d",dp[0][m]); 
	return 0;
}