【ytboj】【最小生成树】最小距离和

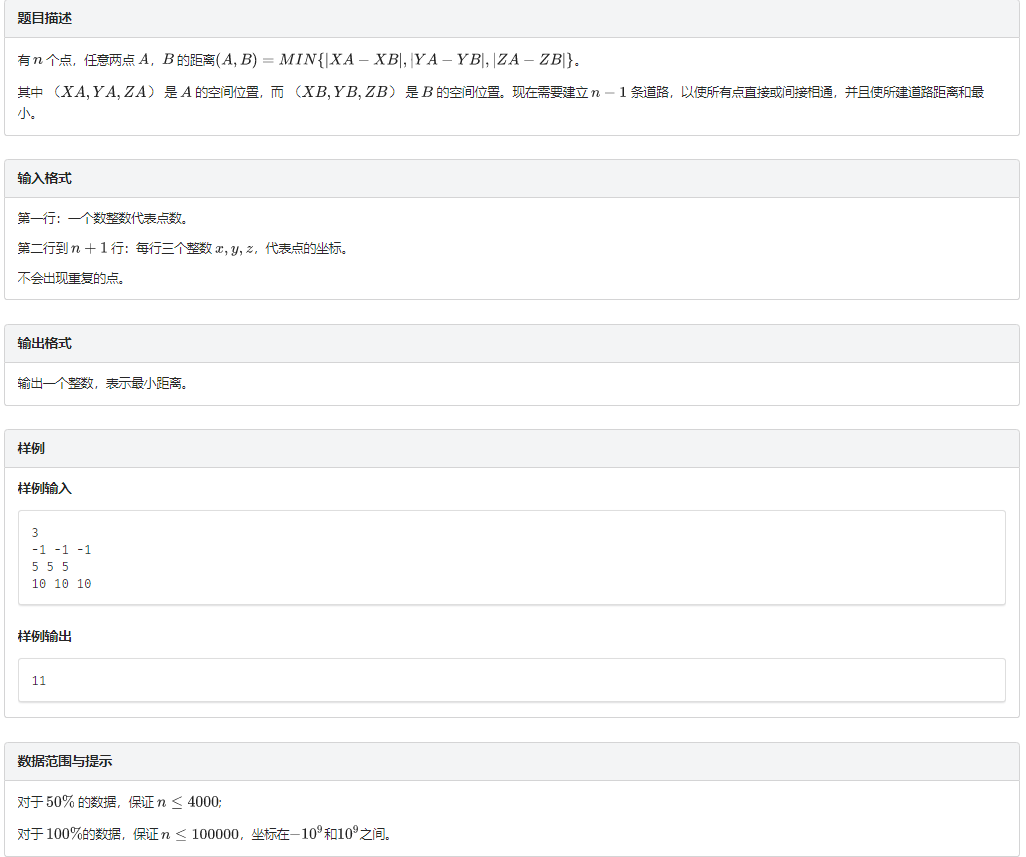
题意

题解

之前一直以为prim堆优化之后复杂度是O(nlogn)...YY了一发之后不出所料的60pts TLE了qwq（实际上是O(n+m)logn）

算法复杂度高的原因建了很多不必要的边

对于每一维空间，只有相邻的两个点才会建边，所以总边数=n*3

再跑kruskal或者prim都可以了

关键：把状态拆分，分层讨论

代码

最小距离和【60pts】

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mp make_pair
#define pr pair<ll,int>
priority_queue<pr,vector<pr>,greater<pr> >q; 
const int INF = 0x3f3f3f3f,N = 1e5+10;
int n,ecnt=-1,vis[N],fa[N];
ll dis[N],ans;
struct point 
{
	int x,y,z;
}a[N];
inline ll Min(int i,int j)
{
	return min(min(abs(a[i].x-a[j].x),abs(a[i].y-a[j].y)),abs(a[i].z-a[j].z));
}
void prim()
{
	for(int i=1;i<=n;i++) dis[i]=1e18;
	dis[1]=0;
	q.push(mp(0,1));
	while(!q.empty())
	{
		int u=q.top().second;q.pop();
		if(vis[u]) continue;
		vis[u]=1,ans+=dis[u];
		for(int i=1;i<=n;i++)
		{
			int v=i;
			if(vis[v]||v==u) continue;
			if(dis[v]>Min(u,v))
			{
				//printf("(u,v):%d %d
",u,v);
				dis[v]=Min(u,v);
				q.push(mp(dis[v],v));
			}
		}
	}
}
int main()
{
	//memset(head,-1,sizeof(head));
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
	prim();
	printf("%lld",ans);
	return 0;
}

最小距离和【AC】

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const int INF = 0x3f3f3f3f,N = 1e5+10;
int n,m,f[N],cnt;
ll ans;
struct edge
{
	int x,y;
	ll w;
	inline bool operator < (const edge oth) const 
	{
		return w<oth.w;
	}
}dis[N<<2];
struct point 
{
	int x,y,z,id;
}a[N];
bool cmp1(point a,point b) {return a.x<b.x;}
bool cmp2(point a,point b) {return a.y<b.y;}
bool cmp3(point a,point b) {return a.z<b.z;}
void init(){for(int i=1;i<=n;i++) f[i]=i;}
int find(int x)
{
	if(f[x]==x) return x;
	return f[x]=find(f[x]);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
		a[i].id=i;
	}
	init();
	sort(a+1,a+n+1,cmp1);
	for(int i=1;i<n;i++)
		dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].x-a[i+1].x)};
	sort(a+1,a+n+1,cmp2);
	for(int i=1;i<n;i++)
		dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].y-a[i+1].y)};
	sort(a+1,a+n+1,cmp3);
	for(int i=1;i<n;i++)
		dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].z-a[i+1].z)};
	sort(dis+1,dis+cnt+1);
	int ecnt=0;
	for(int i=1;i<=cnt;i++)
	{
		int x=dis[i].x,y=dis[i].y;
		if(find(x)!=find(y))
		{
			f[f[x]]=f[y];
			ans+=dis[i].w;
			ecnt++;
		}
		if(ecnt==n-1) break;
	}
	printf("%lld",ans);
	return 0;
}