【ybtoj】【最小生成树】保留道路

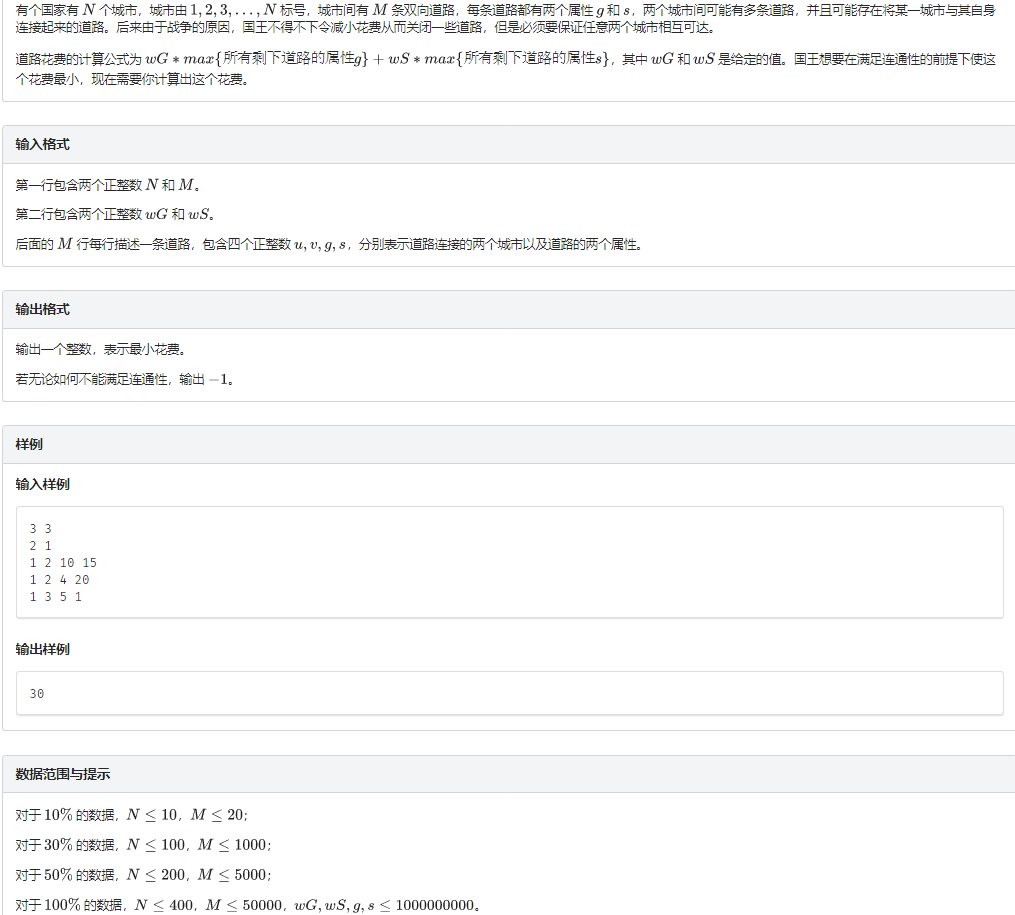
题意

题解

这题我一开始根本没有思路....因为觉得 s , g 两个量会互相影响，没法做最小生成树（其实也是因为没认真看数据范围）

先想暴力：

多个变量可以“定一移一”，就是枚举其中一个的最大值，然后讨论另一个变量（在这里“讨论”就是做最小生成树）

考虑把 g 从小到大排序，每次对小于当前 maxg 的边求最小生成树，复杂度O(m²logm）

考虑优化

• 每次新加入的边只有一条，可以优化排序过程变成O(m²)
• 每次做最小生成树的边最多只有 n 条，即当前加入的新边和原先最小生成树的 n-1 条边
• 复杂度降至O(nm)，可以通过此题

关键：考虑如何消除其中一个变量的影响，在暴力的基础上进行优化

代码

保留道路

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,M = 1e5+10,N = 405;
int n,m,f[N],cntn,wss,wg;
ll ans=(ll)INF*INF;
struct edge
{
	int x,y,g,s;
}a[M],now[M];
bool cmp(edge a,edge b)
{
	return a.g<b.g;
}
void init()
{
	for(int i=1;i<=n;i++) f[i]=i;
}
int find(int x)
{
	if(f[x]==x) return x;
	return f[x]=find(f[x]);
}
void kruskal()
{
	init();
	int cnt=0,maxg=0;
	for(int i=1;i<=cntn;i++)	
	{
		int x=now[i].x,y=now[i].y;
		if(find(x)!=find(y))
			f[f[x]]=f[y],now[++cnt]=now[i],maxg=max(maxg,now[i].g);
		if(cnt==n-1) {ans=min(ans,1ll*now[i].s*wss+1ll*maxg*wg),cntn=cnt;return;}
	}
	return;
}

int main()
{
	scanf("%d%d%d%d",&n,&m,&wg,&wss);
	for(int i=1;i<=m;i++)
	{
		int u,v,g,s;
		scanf("%d%d%d%d",&u,&v,&g,&s);
		a[i]=(edge){u,v,g,s};
	}
	sort(a+1,a+m+1,cmp);
	for(int i=1;i<=m;i++)
	{
		now[++cntn]=a[i];
		for(int j=cntn;j>=2;j--)
			if(now[j].s<now[j-1].s) swap(now[j],now[j-1]);//类似冒泡排序 
		if(cntn>=n-1) kruskal();//cnt最终取值都是n,n-1左右 
		//printf("%d
",ans);
	}
	if(ans==(ll)INF*INF) printf("-1");
	else printf("%lld",ans); 
	return 0;
}