Description
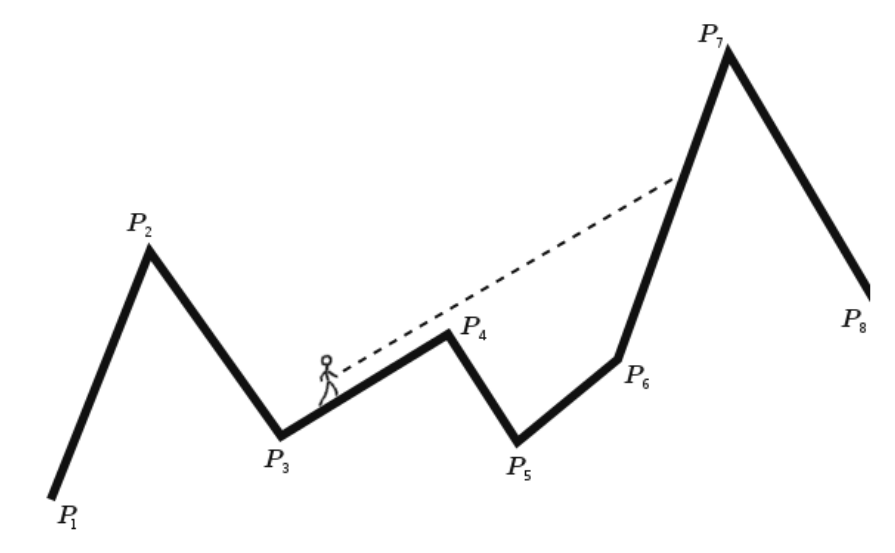
现在在平面上给你一条折线P1P2P3...Pn。
x坐标是严格单调递增的。对于每一段折线PiPi+1,请你找一个最小的j,使得j>i且走在PiPi+1的人能看到折线PjPj+1上的任意一点。
注意,人的高度无限趋近0但不可忽略。也就是说,请找一条编号最小的折线PiPi+1使得j>i且线段PiPi+1(含端点)与略高于PiPi+1的射线相交。
$2leq nleq 10^{5}$
$0leq x_{i},y_{i}leq 10^{9}$
Solution
定义折线i为PiPi+1
首先,对于某条折线i,我们无法通过某些公式或比较直接推定它对应的折线j。
遇到这种情况,我们一般先考虑二分。及对于某条折线i,区间[l,r]之间是否有解。
显然这里的判断可以使用凸包。只要该折线与点区间[l,r]之间的凸包上某条边有交点(当然要注意特判,假如折线与凸包交在顶点要算顶点后面的边),则我们可以判定i在[l,r]之间有解。所以用线段树维护凸包,查询时先查询线段树左区间,左区间无解再找右边。在凸包上的判断也可以用二分。(这个的具体判断方法见代码,画个图就好,证明可以利用叉积的几何意义)
我的代码中,区间[l,r]表示的是点集[l,r+1],这样就可以确保最终答案是找到一条折线而不是一个点。
Code
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; typedef long long ll; int n; struct P{int x,y; friend P operator-(P a,P b){return P{a.x-b.x,a.y-b.y};} friend ll operator*(P a,P b){return 1ll*a.x*b.y-1ll*a.y*b.x;} }p[100010],st[2000010];int tp=0; int _l[400010],_r[400010]; void seg_build(int k,int l,int r) { _l[k]=tp+1; for(int i=l;i<=r+1;i++) { while (tp-_l[k]>0&&(st[tp]-st[tp-1])*(p[i]-st[tp])>=0) tp--; st[++tp]=p[i]; } _r[k]=tp; if (l==r) return; int mid=(l+r)/2; seg_build(k<<1,l,mid); seg_build(k<<1|1,mid+1,r); } bool check(int k,int id) { P a=p[id],v=p[id+1]-a; int l=_l[k],r=_r[k]-1,mid; while (l<r) { mid=(l+r)/2; if ((st[mid]-a)*v<(st[mid+1]-a)*v) r=mid; else l=mid+1; } return (st[l]-a)*v<0||(st[l+1]-a)*v<0; } int query(int k,int l,int r,int ask) { if (ask<=l) { if (!check(k,ask-1)) return 0; if (l==r) return l; } int mid=(l+r)/2; if (ask<=mid) { int re=query(k<<1,l,mid,ask); if (re) return re; } return query(k<<1|1,mid+1,r,ask); } int main() { scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d%d",&p[i].x,&p[i].y); seg_build(1,1,n-1); for (int i=1;i<n-1;i++) printf("%d ",query(1,1,n-1,i+1)); printf("0"); }