在上一篇的一般线性回归中,使用的假设函数是一元一次方程,也就是二维平面上的一条直线。但是很多时候可能会遇到直线方程无法很好的拟合数据的情况,这个时候可以尝试使用多项式回归。多项式回归中,加入了特征的更高次方(例如平方项或立方项),也相当于增加了模型的自由度,用来捕获数据中非线性的变化。添加高阶项的时候,也增加了模型的复杂度。随着模型复杂度的升高,模型的容量以及拟合数据的能力增加,可以进一步降低训练误差,但导致过拟合的风险也随之增加。
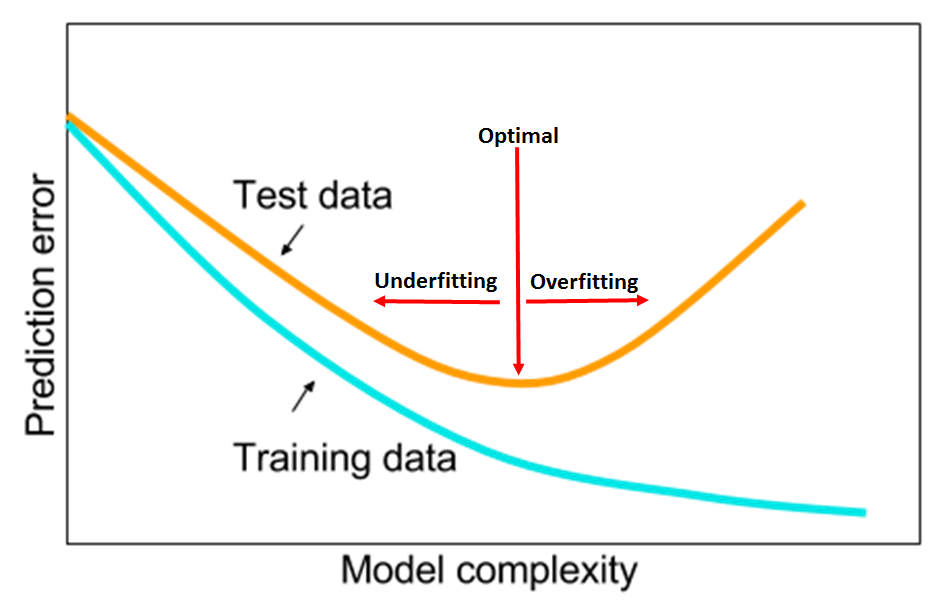
图A,模型复杂度与训练误差及测试误差之间的关系

在这里有个问题在刚开始学习线性回归的时候困扰了自己很久:如果假设中出现了高阶项,那么这个模型还是线性模型吗?此时看待问题的角度不同,得到的结果也不同。如果把上面的假设看成是特征xx的方程,那么该方程就是非线性方程;如果看成是参数θθ的方程,那么xx的高阶项都可以看做是对应θθ的参数,那么该方程就是线性方程。很明显,在线性回归中采用了后一种解释方式。因此多项式回归仍然是参数的线性模型。
1. 多项式回归的实现
下面主要使用了numpy、scipy、matplotlib和scikit-learn,所有使用到的函数的导入如下:
1 import numpy as np 2 from scipy import stats 3 import matplotlib.pyplot as plt 4 from sklearn.preprocessing import PolynomialFeatures 5 from sklearn.linear_model import LinearRegression 6 from sklearn.metrics import mean_squared_error
下是使用的数据是使用y=x2+2y=x2+2并加入一些随机误差生成的,只取了10个数据点:
1 data = np.array([[ -2.95507616, 10.94533252],
2 [ -0.44226119, 2.96705822],
3 [ -2.13294087, 6.57336839],
4 [ 1.84990823, 5.44244467],
5 [ 0.35139795, 2.83533936],
6 [ -1.77443098, 5.6800407 ],
7 [ -1.8657203 , 6.34470814],
8 [ 1.61526823, 4.77833358],
9 [ -2.38043687, 8.51887713],
10 [ -1.40513866, 4.18262786]])
11 m = data.shape[0] # 样本大小
12 X = data[:, 0].reshape(-1, 1) # 将array转换成矩阵
13 y = data[:, 1].reshape(-1, 1)
14 plt.plot(X, y, "b.")
15 plt.xlabel('X')
16 plt.ylabel('y')
17 plt.show()
这些数据点plot出来,如下图:
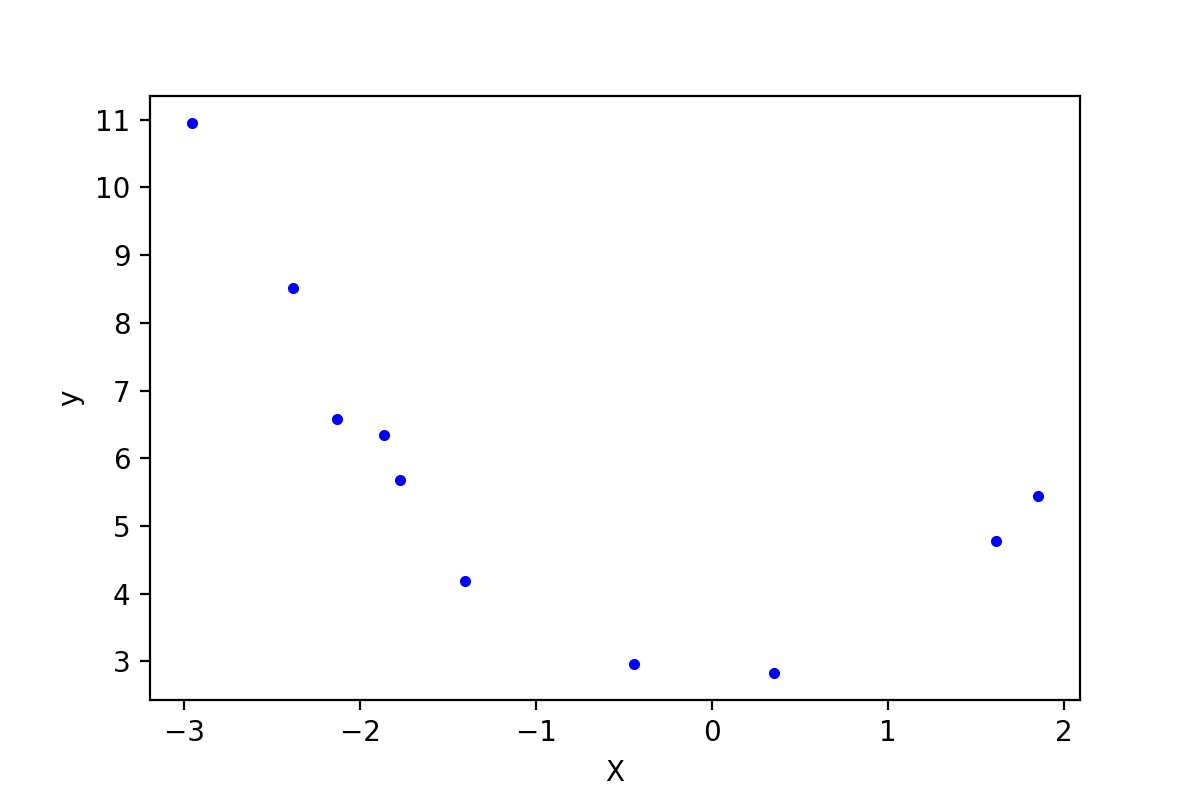
图1-1,原始数据
1.1 直线方程拟合
下面先用直线方程拟合上面的数据点:
1 lin_reg = LinearRegression()
2 lin_reg.fit(X, y)
3 print(lin_reg.intercept_, lin_reg.coef_) # [ 4.97857827] [[-0.92810463]]
4
5 X_plot = np.linspace(-3, 3, 1000).reshape(-1, 1)
6 y_plot = np.dot(X_plot, lin_reg.coef_.T) + lin_reg.intercept_
7 plt.plot(X_plot, y_plot, 'r-')
8 plt.plot(X, y, 'b.')
9 plt.xlabel('X')
10 plt.ylabel('y')
11 plt.savefig('regu-2.png', dpi=200)
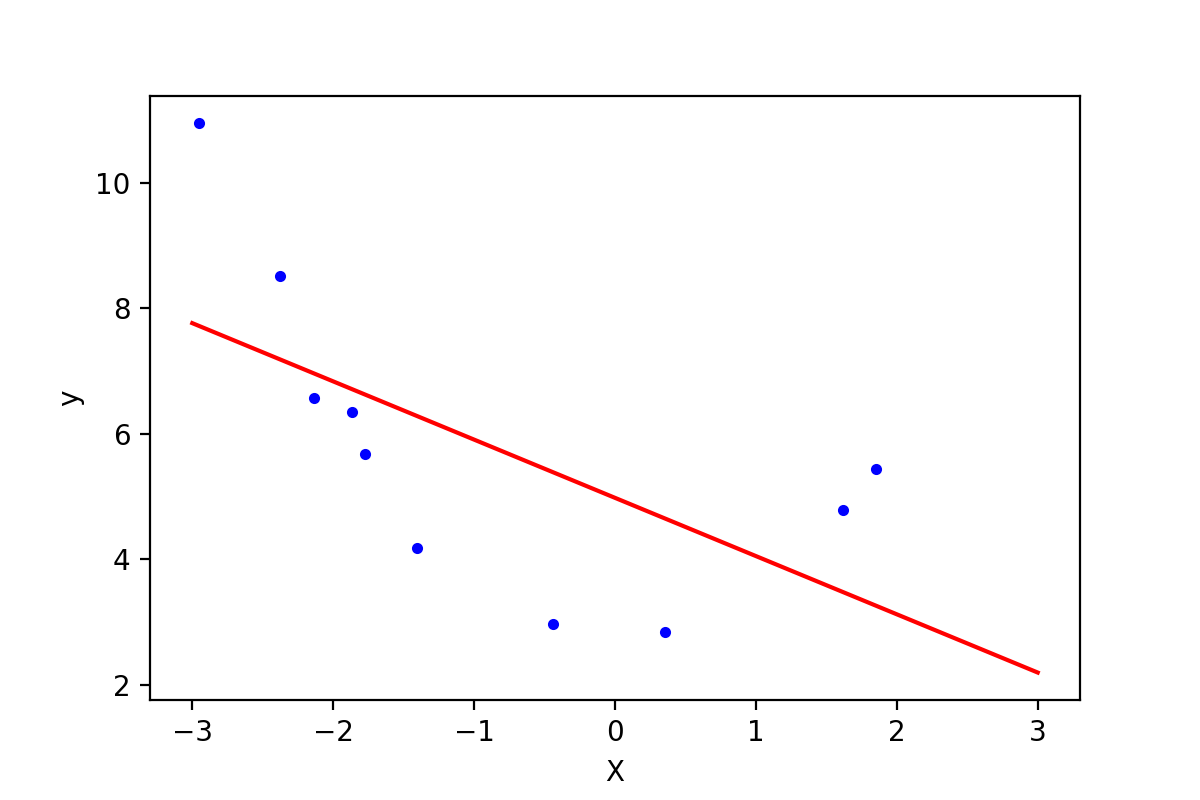
图1-2,直线拟合的效果
可以使用函数"mean_squared_error"来计算误差(使用前面介绍过的Mean squared error, MSE):
h = np.dot(X.reshape(-1, 1), lin_reg.coef_.T) + lin_reg.intercept_ print(mean_squared_error(h, y)) # 3.34
1.2 使用多项式方程
为了拟合2次方程,需要有特征x2x2的数据,这里可以使用函数"PolynomialFeatures"来获得:
1 poly_features = PolynomialFeatures(degree=2, include_bias=False) 2 X_poly = poly_features.fit_transform(X) 3 print(X_poly)
结果如下:
[[-2.95507616 8.73247511] [-0.44226119 0.19559496] [-2.13294087 4.54943675] [ 1.84990823 3.42216046] [ 0.35139795 0.12348052] [-1.77443098 3.1486053 ] [-1.8657203 3.48091224] [ 1.61526823 2.60909145] [-2.38043687 5.66647969] [-1.40513866 1.97441465]]
利用上面的数据做线性回归分析:
1 lin_reg = LinearRegression() 2 lin_reg.fit(X_poly, y) 3 print(lin_reg.intercept_, lin_reg.coef_) # [ 2.60996757] [[-0.12759678 0.9144504 ]] 4 5 X_plot = np.linspace(-3, 3, 1000).reshape(-1, 1) 6 X_plot_poly = poly_features.fit_transform(X_plot) 7 y_plot = np.dot(X_plot_poly, lin_reg.coef_.T) + lin_reg.intercept_ 8 plt.plot(X_plot, y_plot, 'r-') 9 plt.plot(X, y, 'b.') 10 plt.show()
第3行得到了训练后的参数,即多项式方程为h=−0.13x+0.91x2+2.61h=−0.13x+0.91x2+2.61 (结果中系数的顺序与XX中特征的顺序一致),如下图所示:
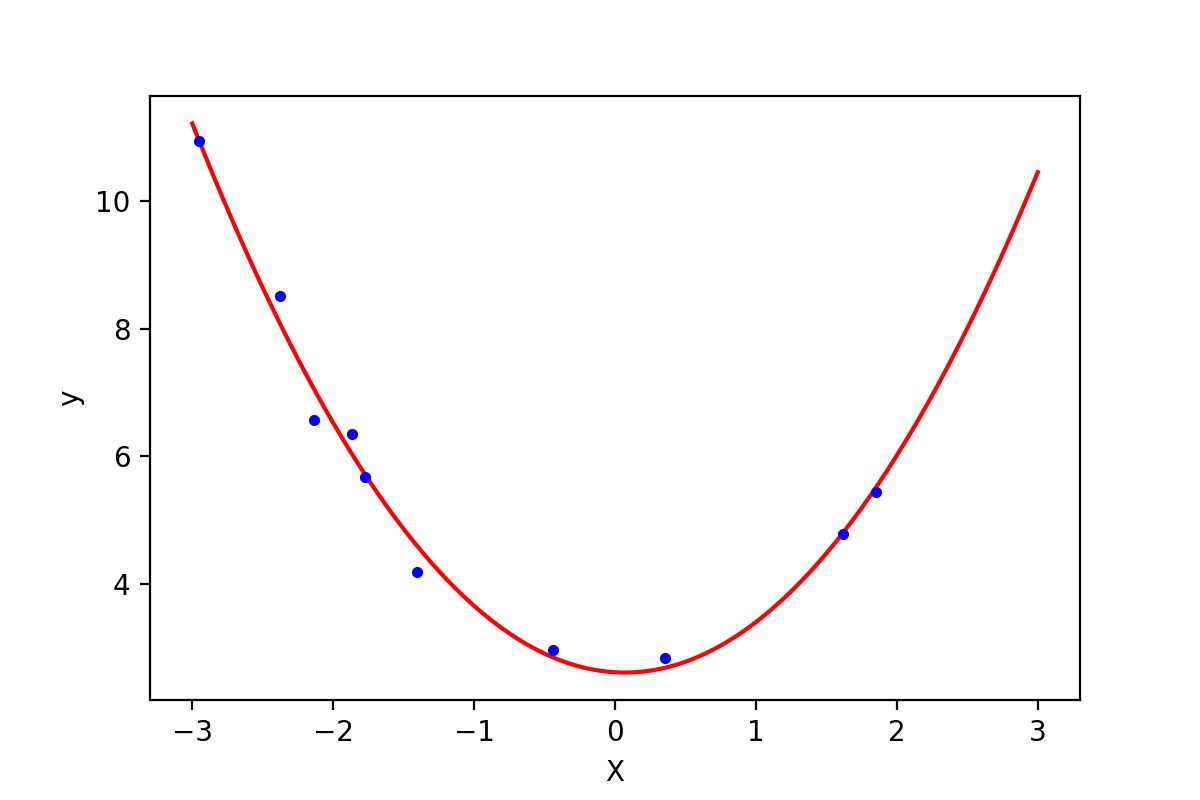
图1-3:2次多项式方程与原始数据的比较
利用多项式回归,代价函数MSE的值下降到了0.07。通过观察代码,可以发现训练多项式方程与直线方程唯一的差别是输入的训练集XX的差别。在训练直线方程时直接输入了XX的值,在训练多项式方程的时候,还添加了我们计算出来的x2x2这个“新特征”的值(由于x2x2完全是由xx的值确定的,因此严格意义上来讲此时该模型只有一个特征xx)。
此时有个非常有趣的问题:假如一开始得到的数据就是上面代码中"X_poly"的样子,且不知道x1x1与x2x2之间的关系。此时相当于我们有10个样本,每个样本具有x1,x2x1,x2两个不同的特征。这时假设函数为:
直接按照二元线性回归方程来训练,也可以得到上面同样的结果(θθ的值)。如果在相同情况下,收集到了新的数据,可以直接带入上面的方程进行预测。唯一不同的是,我们不知道x2=x21x2=x12这个隐含在数据内部的关系,所有也就无法画出图1-3中的这条曲线。一旦了解到了这两个特征之间的关系,数据的维度就从3维下降到了2维(包含截距项θ0θ0)。
2. 持续降低训练误差与过拟合
在上面实现多项式回归的过程中,通过引入高阶项x2x2,训练误差从3.34下降到了0.07,减小了将近50倍。那么训练误差是否还有进一步下降的空间呢?答案是肯定的,通过继续增加更高阶的项,训练误差可以进一步降低。通过尝试,当最高阶项为x11x11时,训练误差为3.11e-23,几乎等于0了。
下面是测试不同degree的过程:
1 # test different degree and return loss
2 def try_degree(degree, X, y):
3 poly_features_d = PolynomialFeatures(degree=degree, include_bias=False)
4 X_poly_d = poly_features_d.fit_transform(X)
5 lin_reg_d = LinearRegression()
6 lin_reg_d.fit(X_poly_d, y)
7 return {'X_poly': X_poly_d, 'intercept': lin_reg_d.intercept_, 'coef': lin_reg_d.coef_}
8
9 degree2loss_paras = []
10 for i in range(2, 20):
11 paras = try_degree(i, X, y)
12 h = np.dot(paras['X_poly'], paras['coef'].T) + paras['intercept']
13 _loss = mean_squared_error(h, y)
14 degree2loss_paras.append({'d': i, 'loss': _loss, 'coef': paras['coef'], 'intercept': paras['intercept']})
15
16 min_index = np.argmin(np.array([i['loss'] for i in degree2loss_paras]))
17 min_loss_para = degree2loss_paras[min_index]
18 print(min_loss_para) #
19 X_plot = np.linspace(-3, 1.9, 1000).reshape(-1, 1)
20 poly_features_d = PolynomialFeatures(degree=min_loss_para['d'], include_bias=False)
21 X_plot_poly = poly_features_d.fit_transform(X_plot)
22 y_plot = np.dot(X_plot_poly, min_loss_para['coef'].T) + min_loss_para['intercept']
23 fig, ax = plt.subplots(1, 1)
24 ax.plot(X_plot, y_plot, 'r-', label='degree=11')
25 ax.plot(X, y, 'b.', label='X')
26 plt.xlabel('X')
27 plt.ylabel('y')
28 ax.legend(loc='best', frameon=False)
29 plt.savefig('regu-4-overfitting.png', dpi=200)
输出为:
{'coef': array([[ 0.7900162 , 26.72083627, 4.33062978, -7.65908434,
24.62696711, 12.33754429, -15.72302536, -9.54076366,
1.42221981, 1.74521649, 0.27877112]]),
'd': 11,
'intercept': array([-0.95562816]),
'loss': 3.1080267005676934e-23}
画出的函数图像如下:
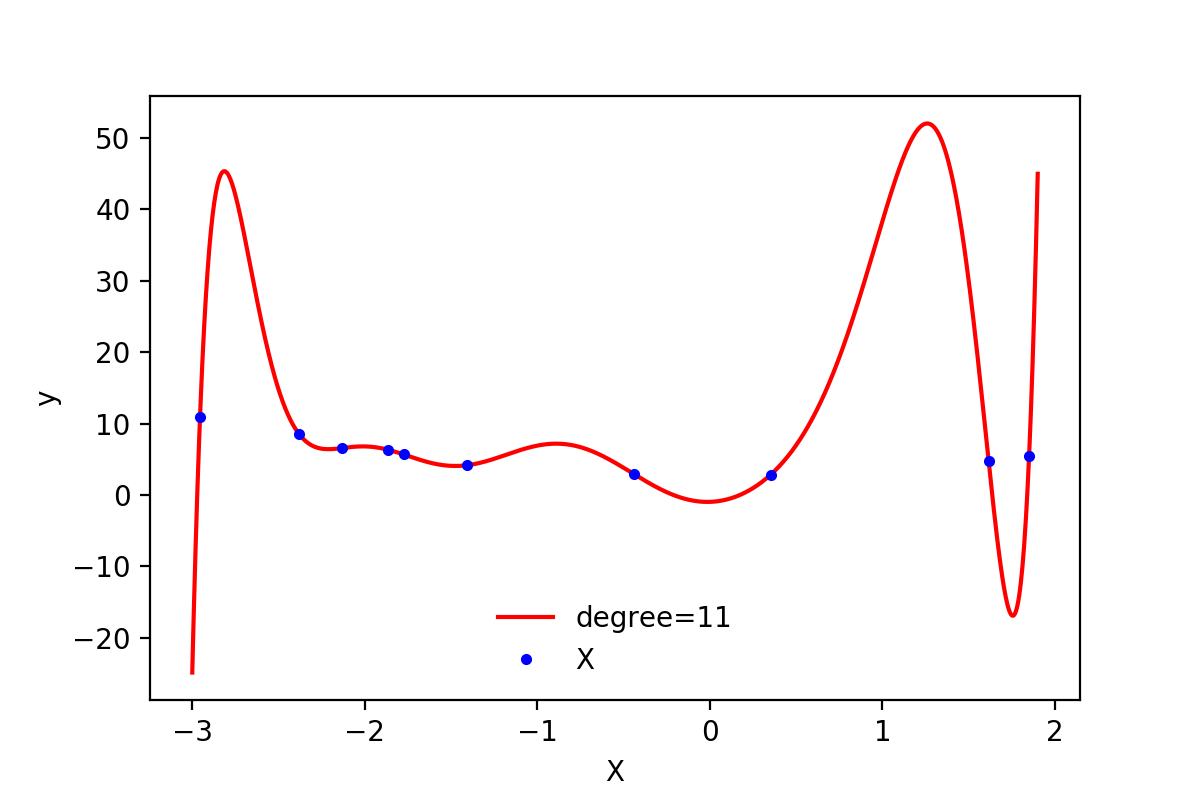
图2-1:degree=11时的函数图像
由图2-1可以看到,此时函数图像穿过了每一个样本点,所有的训练样本都落在了拟合的曲线上,训练误差接近与0。 可以说是近乎完美的模型了。但是,这样的曲线与我们最开始数据的来源(一个二次方程加上一些随机误差)差异非常大。如果从相同来源再取一些样本点,使用该模型预测会出现非常大的误差。类似这种训练误差非常小,但是新数据点的测试误差非常大的情况,就叫做模型的过拟合。过拟合出现时,表示模型过于复杂,过多考虑了当前样本的特殊情况以及噪音(模型学习到了当前训练样本非全局的特性),使得模型的泛化能力下降。
出现过拟合一般有以下几种解决方式:
- 降低模型复杂度,例如减小上面例子中的degree;
- 降维,减小特征的数量;
- 增加训练样本;
- 添加正则化项.
防止模型过拟合是机器学习领域里最重要的问题之一。鉴于该问题的普遍性和重要性,在满足要求的情况下,能选择简单模型时应该尽量选择简单的模型。
Reference
http://scikit-learn.org/stable/modules/linear_model.html
Géron A. Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems[M]. " O'Reilly Media, Inc.", 2017. github
https://www.arxiv-vanity.com/papers/1803.09820/
