x = (x1,...,xn) 和y = (y1,...,yn) 之间的距离为
(1)欧氏距离 EuclideanDistanceMeasure

(2)曼哈顿距离 ManhattanDistanceMeasure
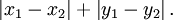
(3)马氏距离MahalanobisDistanceMeasure
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为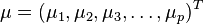 ,协方差矩阵为
,协方差矩阵为 的多变量向量
的多变量向量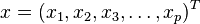 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 的随机变量
的随机变量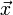 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的欧氏距离。
其中 是
是 的标准差。
的标准差。
(4)余弦距离 CosineDistanceMeasure
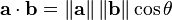
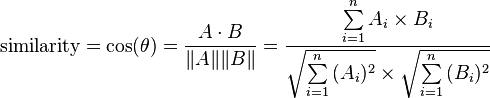
(5)汉明距离
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 例如:
1011101 与1001001 之间的汉明距离是 2。
2143896 与2233796 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
(6)平方欧几里德距离度量 SquaredEuclideanDistanceMeasure

(7)Tanimoto距离 TanimotoDistanceMeasure

(8)加权距离度量 WeightedDistanceMeasure ,具体实现有:WeightedEuclideanDistanceMeasure和WeightedManhattanDistanceMeasure
用欧几里德距离和曼哈顿距离实现。加权距离度量是Mahout的高级特征,它能让你在不同维上赋予不同的权重,以此对距离度量信息产生影响,WeightedDistanceMeasure在向量格式化中需要序列化为文件。变量对距离的影响是不一样的,通过权值来确定。
(9)切比雪夫距离 ChebyshevDistanceMeasure



