4008: [HNOI2015]亚瑟王

2017-08-29

Description

小 K 不慎被 LL 邪教洗脑了，洗脑程度深到他甚至想要从亚瑟王邪教中脱坑。

他决定，在脱坑之前，最后再来打一盘亚瑟王。既然是最后一战，就一定要打得漂亮。众所周知，亚瑟王是一个看脸的游戏，技能的发动都是看概率的。作为一个非洲人，同时作为一个前 OIer，小 K 自然是希望最大化造成伤害的期望值。但他已经多年没写过代码，连 Spaly都敲不对了，因此，希望你能帮帮小 K，让他感受一下当欧洲人是怎样的体验。

本题中我们将考虑游戏的一个简化版模型。

玩家有一套卡牌，共 n张。游戏时，玩家将 n 张卡牌排列成某种顺序，排列后将卡牌按从前往后依次编号为 1 ~ n。本题中，顺序已经确定，即为输入的顺序。每张卡牌都有一个技能。第 i 张卡牌的技能发动概率为 pi，如果成功发动，则会对敌方造成di点伤害。也只有通过发动技能，卡牌才能对敌方造成伤害。基于现实因素以及小K非洲血统的考虑，pi不会为 0，也不会为 1，即 0 < pi < 1。

一局游戏一共有 r 轮。在每一轮中，系统将从第一张卡牌开始，按照顺序依次考虑每张卡牌。在一轮中，对于依次考虑的每一张卡牌：

1如果这张卡牌在这一局游戏中已经发动过技能，则

1.1 如果这张卡牌不是最后一张，则跳过之（考虑下一张卡牌）；否则（是最后一张），结束这一轮游戏。

2否则（这张卡牌在这一局游戏中没有发动过技能），设这张卡牌为第 i 张

2.1将其以 pi的概率发动技能。

2.2如果技能发动，则对敌方造成 di点伤害，并结束这一轮。

2.3如果这张卡牌已经是最后一张（即 i 等于n），则结束这一轮；否则，考虑下一张卡牌。

请帮助小 K 求出这一套卡牌在一局游戏中能造成的伤害的期望值。

Input

输入文件的第一行包含一个整数 T，代表测试数据组数。

接下来一共 T 组数据。

每组数据的第一行包含两个用空格分开的整数 n和r，分别代表卡牌的张数和游戏的轮数。

接下来 n行，每行包含一个实数和一个整数，由空格隔开，描述一张卡牌。第i 行的两个数为 pi和 di，分别代表第 i 张卡牌技能发动的概率（实数）和技能发动造成的伤害（整数）。保证 pi最多包含 4位小数，且为一个合法的概率。

Output

对于每组数据，输出一行，包含一个实数，为这套卡牌在这一局游戏中造成的伤害的期望值。对于每一行输出，只有当你的输出和标准答案的相对误差不超过10^-8时——即|a-o|/a<=10-8时(其中a是标准答案，o是输出)，你的输出才会被判为正确。

建议输出10 位小数。

Sample Input

1
3 2
0.5000 2
0.3000 3
0.9000 1

Sample Output

3.2660250000

这题面有毒……

一个转移方程不好想的dp（反正我是没想出来x）

这个dp就不能求什么设什么了（葵花宝典第一招大失败x）

f[i][j]表示考虑前i张牌，游戏剩余j轮←到达这个状态的概率

从前往后转移

对于每张牌（i+1）

如果这张牌在接下来的j轮都不出，那么考虑下一张，转移到f[i+1][j]，概率是（1-p[i]）^j

如果这张牌在之后的j轮内打了出去，考虑下一轮，转移到f[i+1][j-1]，概率是1-（1-p[i]）^j，打出的伤害加到ans中

(1-p[i])^j可以预处理一下（pw[i][j])

最后就是记得要把f[0][r]设为1（考虑0张牌，还有r轮，游戏刚开始，概率当然是1）

就这样，喵>_<

有哪里没说全的话就丢给s好了

附代码

#include<iostream>
#include<cstdio>
#include<cstring> 
using namespace std;
const int N=250,R=150;
int t,n,r;
double p[N],d[N],f[N][R],pw[N][R]; //f[i][j]=考虑前i张牌，剩余j轮 
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&r);
        for(int i=1;i<=n;++i){scanf("%lf%lf",&p[i],&d[i]);}
        memset(f,0,sizeof(f));
        for(int i=1;i<=n;++i)
        {
            pw[i][0]=1;
            for(int j=1;j<=r;++j)
              pw[i][j]=pw[i][j-1]*(1-p[i]);
        }
        double ans=0;
        f[0][r]=1;
        for(int i=0;i<=n;++i)
        for(int j=0;j<=r;++j)
        {
            f[i+1][j]+=f[i][j]*pw[i+1][j];//没出牌，考虑下一张 
            if(j)
            {
                f[i+1][j-1]+=f[i][j]*(1-pw[i+1][j]);//出牌，考虑下一轮 
                ans+=f[i][j]*(1-pw[i+1][j])*d[i+1];
            }
        }
        printf("%.10lf
",ans);
    }
    return 0;
}

4008(wypx)

by:wypx

总之就是以上了,用w解释的时间我改了一下样例解释。就是看文字太烦了,怎么会有人喜欢阅读那么无聊的东西

样例解释0表示这一轮没有发动spell card

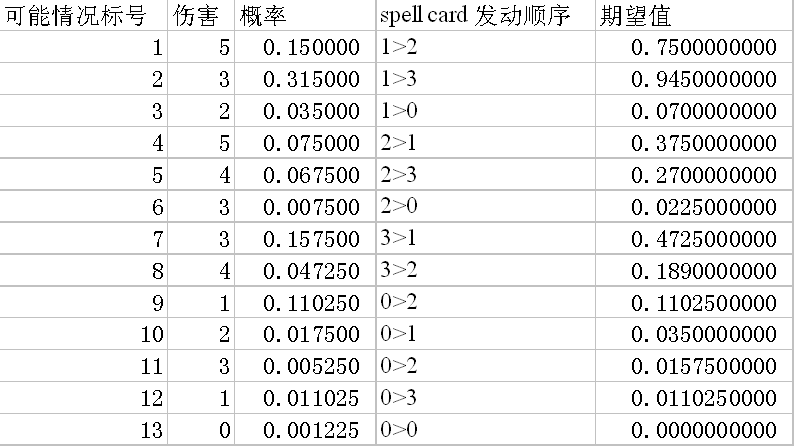
因为是期望,所以先不考虑什么spell card是什么，就单算每一次概率就好了poi

其实把伤害那个拆开,比如5拆成(2+3)*0.15和总共是等价的.(反正对)

就这样了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
using namespace std;
int read(){
    char ch=getchar();
    int an=0,f=1;
    while(!('0'<=ch&&ch<='9')){if(ch=='-')f=-f;else ch=getchar();}
    while('0'<=ch&&ch<='9'){an=an*10+(ch-'0');ch=getchar();}
    return an*f;
}
double p[250],dp[250][250],pw[250][250];
int d[250],n,r,T;
double ans;
void G(){
    for(int i=0;i<=n;i++)p[i]=d[i]=0;
    for(int i=0;i<=n;i++)
        for(int j=0;j<=r;j++)dp[i][j]=pw[i][j]=0;
    ans=0;
}
int main(){
    T=read();
    while(T){T--;
        n=read();r=read();
        for(int i=1;i<=n;i++){scanf("%lf",&p[i]);d[i]=read();}
        for(int i=1;i<=n;i++){
            pw[i][0]=1;
            for(int j=1;j<=r;j++)pw[i][j]=pw[i][j-1]*(1-p[i]);
        }
        dp[0][r]=1;
        for(int i=0;i<n;i++)
            for(int j=0;j<=r;j++){
                dp[i+1][j]+=dp[i][j]*(pw[i+1][j]);
                if(j-1>=0){
                    dp[i+1][j-1]+=dp[i][j]*(1-pw[i+1][j]);
                    ans+=dp[i][j]*d[i+1]*(1-pw[i+1][j]);
                }
            }
    printf("%0.10f
",ans);
    G();
    }
    return 0;
}

s_a_b_e_r

by:s_a_b_e_r

w:小W不慎被LL邪教洗脑了x

s:LL音乐真好听♪,一块来抽UR啊