最小生成树、最短路径

最小生成树：

普里姆算法 和 克鲁斯卡尔算法

普里姆算法：归并顶点，适用稠密网。

克鲁斯卡尔算法：归并边，适用稀疏网。

/******* 普里姆算法（最小生成树） *********/void MiniSpanTree_Prim(AMGraph G, VerTexType u)//最小生成树 普利姆
{
    int i, j, k;
    VerTexType u0, v0;
    k = LocateVex(G, u);
    for (j = 0; j < G.vexnum; ++j)
        if (j != k)
            closedge[j] = { u,G.arcs[k][j] };
    closedge[k].lowcost = 0;
    for (i = 1; i < G.vexnum; ++i)
    {
        k = Min(G);
        u0 = closedge[k].adjvex;
        v0 = G.vexs[k];
        cout << u0 <<"--"<< v0<<"  ";
        closedge[k].lowcost = 0;
        for (j = 0; j < G.vexnum; j++)
            if (G.arcs[k][j] < closedge[j].lowcost)
                closedge[j] = { G.vexs[k],G.arcs[k][j] };
    }
}

/**************克鲁斯卡尔算法 （最小生成树）************/
void MiniSpanTree_Kruskal(AMGraph G) 
{    
    int i, j, v1, v2, vs1, vs2;
    Sort(G);                                             
    for (i = 0; i < G.vexnum; ++i)                         
        Vexset[i] = i;
    for (i = 0; i < G.arcnum; ++i) { 
        v1 = LocateVex(G, Edge[i].Head);                 
        v2 = LocateVex(G, Edge[i].Tail);                 
        vs1 = Vexset[v1];                                
        vs2 = Vexset[v2];                               
        if (vs1 != vs2) {                                 
            cout << Edge[i].Head << "--" << Edge[i].Tail <<"  ";    
            for (j = 0; j < G.vexnum; ++j)              
                if (Vexset[j] == vs2) Vexset[j] = vs1;    
        } 
    }
}

最短路径：

迪杰特斯拉算法和弗洛伊德算法

/**************迪杰特斯拉算法*******************/
void ShortestPath_DIJ(AMGraph G, int v0) {
    //用Dijkstra算法求有向网G的v0顶点到其余顶点的最短路径 
    int v, i, w, min;
    int n = G.vexnum;                                        //n为G中顶点的个数 

    for (v = 0; v < n; ++v) {                                 //n个顶点依次初始化 
        S[v] = false;                                          //S初始为空集 
        D[v] = G.arcs[v0][v];                               //将v0到各个终点的最短路径长度初始化为弧上的权值 
        if (D[v] < MaxInt)  Path[v] = v0;                      //如果v0和v之间有弧，则将v的前驱置为v0 
        else Path[v] = -1;                                   //如果v0和v之间无弧，则将v的前驱置为-1 
    }//for 

    S[v0] = true;                                                //将v0加入S 
    D[v0] = 0;                                                  //源点到源点的距离为0 

                                                                /*―初始化结束，开始主循环，每次求得v0到某个顶点v的最短路径，将v加到S集―*/
    for (i = 1; i < n; ++i) {                                    //对其余n-1个顶点，依次进行计算 
        min = MaxInt;
        for (w = 0; w < n; ++w)
            if (!S[w] && D[w] < min) {                        //选择一条当前的最短路径，终点为v 
                v = w;
                min = D[w];
            }//if             
        S[v] = true;                                           //将v加入S 
        for (w = 0; w < n; ++w)                               //更新从v0出发到集合V?S上所有顶点的最短路径长度 
            if (!S[w] && (D[v] + G.arcs[v][w] < D[w])) {
                D[w] = D[v] + G.arcs[v][w];                   //更新D[w] 
                Path[w] = v;                                  //更改w的前驱为v 
            }//if 
    }//for  
}//ShortestPath_DIJ

弗洛伊德算法：

void ShortestPath_Floyed(AMGraph G){ 
    //用Floyd算法求有向网G中各对顶点i和j之间的最短路径 
    int i , j , k ;
    for (i = 0; i < G.vexnum; ++i)                  //各对结点之间初始已知路径及距离 
        for(j = 0; j < G.vexnum; ++j){ 
            D[i][j] = G.arcs[i][j]; 
            if(D[i][j] < MaxInt && i != j)  Path[i][j]=i;      //如果i和j之间有弧，则将j的前驱置为i 
            else Path [i][j] = -1;                      //如果i和j之间无弧，则将j的前驱置为-1 
        }//for
        for(k = 0; k < G.vexnum; ++k) 
            for(i = 0; i < G.vexnum; ++i) 
                for(j = 0; j < G.vexnum; ++j)
                    if(D[i][k] + D[k][j] < D[i][j]){           //从i经k到j的一条路径更短 
                        D[i][j] = D[i][k]+D[k][j];            //更新D[i][j] 
                        Path[i][j] = Path[k][j];                   //更改j的前驱为k 
                    }//if 
}//ShortestPath_Floyed

我的作业：

#include <iostream>
using namespace std;

#define OK 1
#define MaxInt 32767
#define MVNum 100
typedef int Status;
typedef char VerTexType;
typedef int ArcType;
int visited[MVNum] = { 0 };

typedef struct
{
    VerTexType vexs[MVNum];
    ArcType arcs[MVNum][MVNum];
    int vexnum, arcnum;
}AMGraph;

int LocateVex(AMGraph G, VerTexType u)
{
    int i;
    for (i = 0; i < G.vexnum; ++i)
        if (u == G.vexs[i])
            return i;
    return -1;
}

void DFS_AM(AMGraph G, int v)//深度遍历
{
    cout << G.vexs[v];
    visited[v] = 1;
    for (int w = 0; w < G.vexnum; ++w)
        if ((G.arcs[v][w] != 0) && (!visited[w]))
        {
            DFS_AM(G, w);
        }
}

void DrawLine(int n)
{
    printf("
--+");
    for (int i = 0; i < n; ++i)
    {
        printf("------+");
    }
    printf("
");
}

void Display_AM(AMGraph G)
{
    for (int i = 0; i < G.vexnum; ++i)
        printf("%7c", G.vexs[i]);
    DrawLine(G.vexnum);
    for (int i = 0; i < G.vexnum; ++i)
    {
        printf(" %c|", G.vexs[i]);
        for (int j = 0; j < G.vexnum; ++j)
        {
            printf("%6d|", G.arcs[i][j]);
        }
        DrawLine(G.vexnum);
    }
}

/******* 普里姆算法（最小生成树） *********/
struct 
{
    VerTexType adjvex;
    ArcType lowcost;
}closedge[MVNum];

Status CreateUDN(AMGraph &G)//构造无向网
{
    int i, j, k;
    cout << "请输入总顶点数，总边数，以空格隔开:";
    cin >> G.vexnum >> G.arcnum;
    cout << endl;

    cout << "输入点的名称:";

    for (i = 0; i < G.vexnum; ++i) {
        cin >> G.vexs[i];
    }
    cout << endl;
    for (i = 0; i < G.vexnum; ++i)
        for (j = 0; j < G.vexnum; ++j)
            G.arcs[i][j] = MaxInt;
    for (k = 0; k < G.arcnum; ++k) {
        VerTexType v1, v2;
        ArcType w;
        cout << "请输入第" << (k + 1) << "条边及权值:";
        cin >> v1 >> v2 >> w;
        i = LocateVex(G, v1);  j = LocateVex(G, v2);
        G.arcs[i][j] = w;
        G.arcs[j][i] = G.arcs[i][j];
    }
    return OK;
}


int Min(AMGraph G)
{
    int i;
    int index = -1;
    int min = MaxInt;
    for (i = 0; i < G.vexnum; ++i) {
        if (min > closedge[i].lowcost && closedge[i].lowcost != 0) {
            min = closedge[i].lowcost;
            index = i;
        }
    }
    return index;
}

void MiniSpanTree_Prim(AMGraph G, VerTexType u)//最小生成树 普利姆
{
    int i, j, k;
    VerTexType u0, v0;
    k = LocateVex(G, u);
    for (j = 0; j < G.vexnum; ++j)
        if (j != k)
            closedge[j] = { u,G.arcs[k][j] };
    closedge[k].lowcost = 0;
    for (i = 1; i < G.vexnum; ++i)
    {
        k = Min(G);
        u0 = closedge[k].adjvex;
        v0 = G.vexs[k];
        cout << u0 <<"--"<< v0<<"  ";
        closedge[k].lowcost = 0;
        for (j = 0; j < G.vexnum; j++)
            if (G.arcs[k][j] < closedge[j].lowcost)
                closedge[j] = { G.vexs[k],G.arcs[k][j] };
    }
}

/**************克鲁斯卡尔算法 （最小生成树）************/

struct
{
    VerTexType Head;
    VerTexType Tail;
    ArcType lowcost;
}Edge[MVNum];

int Vexset[MVNum];

Status CreateUDN_Kruskal(AMGraph &G)
{
    int i, j, k;
    cout << "请输入总顶点数，总边数，以空格隔开:";
    cin >> G.vexnum >> G.arcnum;
    cout << endl;

    cout << "输入点的名称:";

    for (i = 0; i < G.vexnum; ++i) {
        cin >> G.vexs[i];
    }
    cout << endl;
    for (i = 0; i < G.vexnum; ++i)
        for (j = 0; j < G.vexnum; ++j)
            G.arcs[i][j] = MaxInt;
    for (k = 0; k < G.arcnum; ++k) {
        VerTexType v1, v2;
        ArcType w;
        cout << "请输入第" << (k + 1) << "条边及权值:";
        cin >> v1 >> v2 >> w;
        i = LocateVex(G, v1);  j = LocateVex(G, v2);
        G.arcs[i][j] = w;
        G.arcs[j][i] = G.arcs[i][j];
        Edge[k].lowcost = w;
        Edge[k].Head = v1;
        Edge[k].Tail = v2;
    }
    return OK;
}

void Sort(AMGraph G)//冒泡排序 
{
    int m = G.arcnum - 2;
    int flag = 1;
    while ((m > 0) && flag == 1) {
        flag = 0;
        for (int j = 0; j <= m; j++) {
            if (Edge[j].lowcost > Edge[j + 1].lowcost) {
                flag = 1;

                VerTexType temp_Head = Edge[j].Head;
                Edge[j].Head = Edge[j + 1].Head;
                Edge[j + 1].Head = temp_Head;


                VerTexType temp_Tail = Edge[j].Tail;
                Edge[j].Tail = Edge[j + 1].Tail;
                Edge[j + 1].Tail = temp_Tail;

                ArcType temp_lowcost = Edge[j].lowcost;
                Edge[j].lowcost = Edge[j + 1].lowcost;
                Edge[j + 1].lowcost = temp_lowcost;
            }
        }
        --m;
    }
}

void MiniSpanTree_Kruskal(AMGraph G) 
{    
    int i, j, v1, v2, vs1, vs2;
    Sort(G);                                             
    for (i = 0; i < G.vexnum; ++i)                         
        Vexset[i] = i;
    for (i = 0; i < G.arcnum; ++i) { 
        v1 = LocateVex(G, Edge[i].Head);                 
        v2 = LocateVex(G, Edge[i].Tail);                 
        vs1 = Vexset[v1];                                
        vs2 = Vexset[v2];                               
        if (vs1 != vs2) {                                 
            cout << Edge[i].Head << "--" << Edge[i].Tail <<"  ";    
            for (j = 0; j < G.vexnum; ++j)              
                if (Vexset[j] == vs2) Vexset[j] = vs1;    
        } 
    }
}


/**************迪杰特斯拉算法*******************/

void ShortestPath_DIJ(AMGraph G, int v0) {
    //用Dijkstra算法求有向网G的v0顶点到其余顶点的最短路径 
    int v, i, w, min;
    int n = G.vexnum;                                        //n为G中顶点的个数 

    for (v = 0; v < n; ++v) {                                 //n个顶点依次初始化 
        S[v] = false;                                          //S初始为空集 
        D[v] = G.arcs[v0][v];                               //将v0到各个终点的最短路径长度初始化为弧上的权值 
        if (D[v] < MaxInt)  Path[v] = v0;                      //如果v0和v之间有弧，则将v的前驱置为v0 
        else Path[v] = -1;                                   //如果v0和v之间无弧，则将v的前驱置为-1 
    }//for 

    S[v0] = true;                                                //将v0加入S 
    D[v0] = 0;                                                  //源点到源点的距离为0 

                                                                /*―初始化结束，开始主循环，每次求得v0到某个顶点v的最短路径，将v加到S集―*/
    for (i = 1; i < n; ++i) {                                    //对其余n-1个顶点，依次进行计算 
        min = MaxInt;
        for (w = 0; w < n; ++w)
            if (!S[w] && D[w] < min) {                        //选择一条当前的最短路径，终点为v 
                v = w;
                min = D[w];
            }//if             
        S[v] = true;                                           //将v加入S 
        for (w = 0; w < n; ++w)                               //更新从v0出发到集合V?S上所有顶点的最短路径长度 
            if (!S[w] && (D[v] + G.arcs[v][w] < D[w])) {
                D[w] = D[v] + G.arcs[v][w];                   //更新D[w] 
                Path[w] = v;                                  //更改w的前驱为v 
            }//if 
    }//for  
}//ShortestPath_DIJ

void DisplayPath(AMGraph G, int begin, int temp) {
    //显示最短路
    if (Path[temp] != -1) {
        DisplayPath(G, begin, Path[temp]);
        cout << G.vexs[Path[temp]] << "-->";
    }
}

测试：

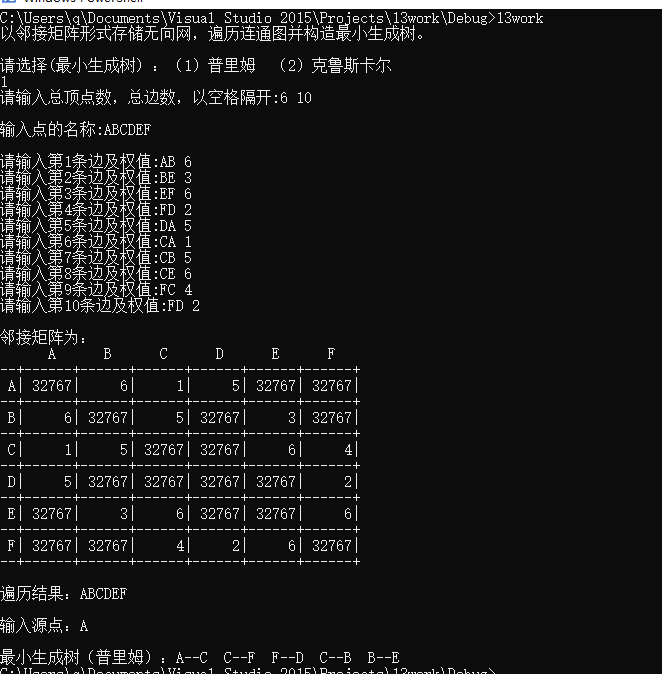
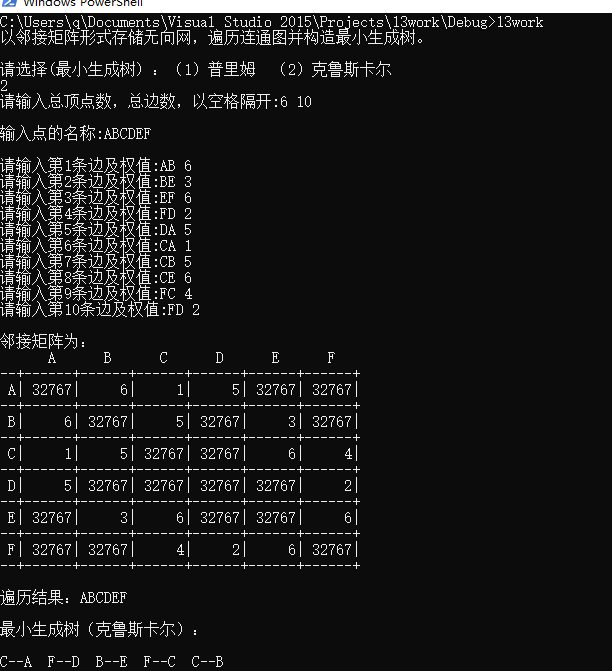
int main()
{
    cout << "以邻接矩阵形式存储无向网，遍历连通图并构造最小生成树。" << endl;
    AMGraph G;
    cout << "
请选择(最小生成树) ：（1）普里姆  （2）克鲁斯卡尔" << endl;
    int a;
    cin >> a;
    if (a == 1)
    {
        CreateUDN(G);
        cout << "
邻接矩阵为：" << endl;
        Display_AM(G);
        cout << "
遍历结果：";
        DFS_AM(G, 0);
        cout << endl;
        VerTexType u;
        cout << "
输入源点：";
        cin >> u;
        cout << "
最小生成树（普里姆）：";
        MiniSpanTree_Prim(G, u);
    }
    else if (a == 2)
    {
        CreateUDN_Kruskal(G);
        cout << "
邻接矩阵为：" << endl;
        Display_AM(G);
        cout << "
遍历结果：";
        DFS_AM(G, 0);
        cout << endl;
        cout << "
最小生成树（克鲁斯卡尔）：
";
        cout << endl;
        MiniSpanTree_Kruskal(G);
    }
    cout << endl;

    int num_start, num_destination;
    VerTexType start, destination;
    cout << "请依次输入起始点、终点名称：";
    cin >> start >> destination;
    num_start = LocateVex(G, start);
    num_destination = LocateVex(G, destination);
    ShortestPath_DIJ(G, num_start);
    cout << endl << "最短路径为：";
    DisplayPath(G, num_start, num_destination);
    cout << G.vexs[num_destination] << endl;

    return 0;
}

运行结果：