链接:http://211.140.156.254:2333/contest/67
转眼间上次加回来的Rating又掉完了。
这次不知为何特别水,T1想了一段时间没想出来弃了,导致后面心态炸了。
T2也没有注意到有随机数据,少得了10分。
T3也没想过,直接输了些样例再手算了一组数据就没管了。
然而考完发现T1一直卡在一个坑里跳不出来,但很多人都A了T1而我只有30分。
所以一夜回到解放前。
T1 实际上是一道分治大水题。
我们先令a[i]=i;然后这当然是不满足要求的。
所以我们每次取出队列中的一半数字(下标为奇数),再取出另一半数字(下标为偶数)分别组成新的队列。
然后单独分治即可,这里给一个图理解一下:
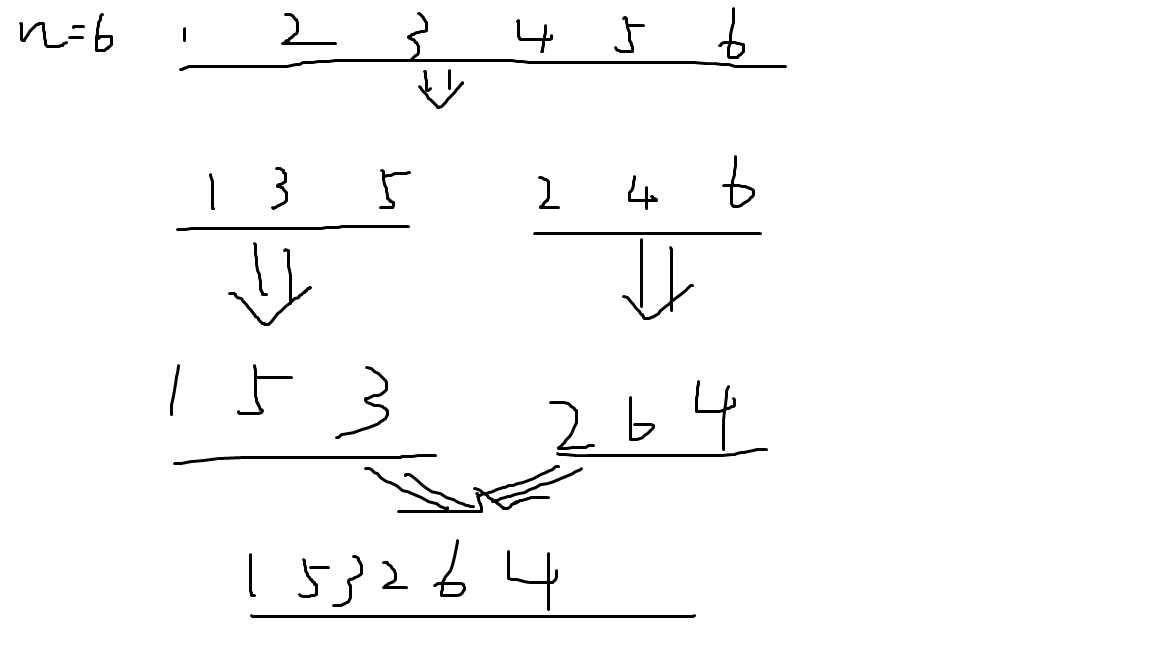
所以对于n=6时,序列就是153264
由于是分而治之,因此复杂度为O(n log n)
T2 01串hash+线段树。
考虑O(n^2)的暴力,每次找出两个数i,j,然后把它们作为等差数列的前两项,然后查找第三项的位置是否合法。
然后只要加上一大堆类似clock之类的玄学操作竟然可以A了
然后考虑正解。对于读入的数x,如果x-k和x+k在之前都出现过(或都没出现过),那么是合法的。反之,若其中只有一个数出现过,那么必然会出现x-k,x,x+k或x+k,x,x-k这样的情况,就不是反等差数列。
因此我们再细化一点,用01串表示在x之前所有数的出现情况(出现就为1)
然后对它的性质进行分析可以发现当且仅当这个串在边界范围内以x为中心左右对称才合法。
例如(令当前的数为x):
当串为:1101x1011或1101x101110是都是合法的(后者前面4个数就到边界了,众所周知数的范围在1至n,没有负数之类的东西)
当串为:1011x1011或11011x11010时都是不合法的
然后对于所有的01串进行hash再判重即可。
但是单纯的hash会T,所以用线段树来维护hash
具体实现看代码,这里线段树要有3个信息:
len:子树大小,主要是为了hash
lh:从左向右的hash顺序时当前节点的值
rh:从右向左的hash顺序时当前节点的值
对于hash可以开unsighed long long自然溢出,这样比较方便。同时记得把次数预处理出来。
CODE
#include<cstdio> using namespace std; typedef unsigned long long uni; const int N=200005; struct segtree { int len; uni lh,rh; }tree[N<<2]; int n,x,last; uni h1,h2,seed[N]; inline char tc(void) { static char fl[100000],*A=fl,*B=fl; return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++; } inline void read(int &x) { x=0; char ch=tc(); while (ch<'0'||ch>'9') ch=tc(); while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc(); } inline int min(int a,int b) { return a<b?a:b; } inline void build(int root,int l,int r) { if (l==r) { tree[root].len=1; return; } int mid=l+r>>1; build(root<<1,l,mid); build(root<<1|1,mid+1,r); tree[root].len=tree[root<<1].len+tree[root<<1|1].len; } inline void updata(int root) { tree[root].lh=tree[root<<1].lh*seed[tree[root<<1|1].len]+tree[root<<1|1].lh; tree[root].rh=tree[root<<1|1].rh*seed[tree[root<<1].len]+tree[root<<1].rh; } inline void modify(int root,int l,int r,int id) { if (l==r) { tree[root].lh=tree[root].rh=1; return; } int mid=l+r>>1; if (id<=mid) modify(root<<1,l,mid,id); if (id>mid) modify(root<<1|1,mid+1,r,id); updata(root); } inline void l_query(int root,int l,int r,int beg,int end) { if (beg<=l&&end>=r) { h1+=tree[root].lh*seed[last]; last+=tree[root].len; return; } int mid=l+r>>1; if (end>mid) l_query(root<<1|1,mid+1,r,beg,end); if (beg<=mid) l_query(root<<1,l,mid,beg,end); } inline void r_query(int root,int l,int r,int beg,int end) { if (beg<=l&&end>=r) { h2+=tree[root].rh*seed[last]; last+=tree[root].len; return; } int mid=l+r>>1; if (beg<=mid) r_query(root<<1,l,mid,beg,end); if (end>mid) r_query(root<<1|1,mid+1,r,beg,end); } int main() { //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout); register int i; read(n); build(1,1,n); for (seed[0]=1,i=1;i<=n;++i) seed[i]=seed[i-1]*233; for (i=1;i<=n;++i) { read(x); modify(1,1,n,x); int len=min(x-1,n-x); if (!len) continue; last=0; h1=0; l_query(1,1,n,x-len,x-1); last=0; h2=0; r_query(1,1,n,x+1,x+len); if (h1!=h2) { puts("NO"); return 0; } } puts("YES"); return 0; }
T3 搜索+打表。
然而当我看到这道题时觉得很不可做,输了样例等弄了7分。
实际上要发现一个性质:当一个串的左右括号的数量相等时必然是一个合法的括号序列的循环移位。
所以爆搜一些小的点,然后用组合数学推一下其中一个等于2时的情况就可以拿不少分。
这里对于标算的判重和思路不是很懂,所以还是只会30分左右的搜索。
CODE
#include<cstdio> using namespace std; const int N=20,mod=998244353; int h[N][2],l[N][2],a,b,ans; inline void check(void) { for (register int i=1;i<=a;++i) if (h[i][0]!=h[i][1]) return; for (register int j=1;j<=b;++j) if (l[j][0]!=l[j][1]) return; if (++ans>=mod) ans-=mod; } inline void DFS(int x,int y) { if (x>a) { check(); return; } if (h[x][0]>b/2||h[x][1]>b/2) return; if (l[y][1]>a/2||l[y][1]>a/2) return; int xx=x,yy=y; if (++yy>b) ++xx,yy=1; ++h[x][0]; ++l[y][0]; DFS(xx,yy); --h[x][0]; --l[y][0]; ++h[x][1]; ++l[y][1]; DFS(xx,yy); --h[x][1]; --l[y][1]; } int main() { scanf("%d%d",&a,&b); DFS(1,1); printf("%d",ans); return 0; }