BZOJ #4771. 七彩树

感谢陈指导的倾情指导，教会了我这题

首先我们考虑如果询问的是子树内的答案应该怎么做

首先对于数颜色的问题，肯定要考虑树上差分。我们刚开始设每个点点权为(1)，每次统计子树内的点权和

考虑差分去除重复的颜色的贡献，很显然我们对于两个相同颜色的点(x,y)，它们的LCA处显然需要减(1)

但是直接统计点对显然又会算重，这里用和类似于虚树建树的方式，将同颜色的点按DFS序排序后在相邻两点的LCA处减去贡献即可

接下来考虑带上深度的限制怎么做，刚开始我们有一个很naive的想法

动态开点线段树维护子树内以深度为下标的贡献，向上线段树合并即可

但是这样会有一种反例，例如对于这种情况：

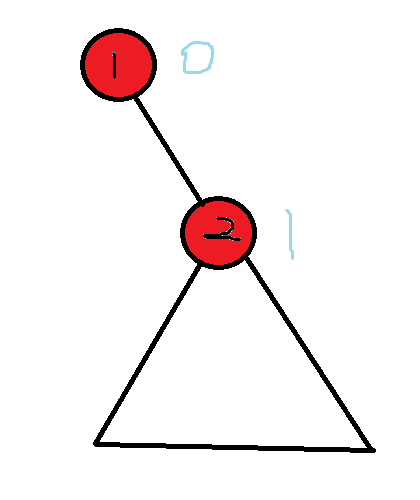
显然我们预处理之后它们的点权分别是(0,1)，但是如果我们询问(1)号点的答案时显然不是(0)

受此启发，我们发现点加入的顺序会对答案产生影响，再观察一下询问就会发现它询问的其实都是在深度小于某个数时的答案

换句话说，我们需要按照深度的顺序从小到大来处理，就可以避免上面的那种情况

我们考虑依次枚举深度(i)，每次将(dep_x=i)的点加入，那么考虑此时我们差分LCA的贡献时需要维护一个关于DFS序的前驱和后继，对每种颜色开一个set动态维护即可

然后现在我们只需要知道当加入的点深度(le i)时的答案，显然深度为(i)的情况可以从(i-1)继承过来，用主席树维护即可

#include<cstdio>
#include<set>
#include<iostream>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
typedef vector <int>::iterator VI;
const int N=100005,P=18;
struct edge
{
	int to,nxt;
}e[N]; int t,n,m,cnt,head[N],c[N],x,y,idx,ans,L[N],R[N],dep[N],mxd;
struct element
{
	int x,y; //x:dfn y:id
	inline element(CI X=0,CI Y=0) { x=X; y=Y; }
	friend inline bool operator < (const element& A,const element& B)
	{
		return A.x<B.x;
	}
}; set <element> s[N]; vector <int> d[N];
typedef set <element>::iterator SI;
inline void addedge(CI x,CI y)
{
	e[++cnt]=(edge){y,head[x]}; head[x]=cnt;
}
#define to e[i].to
class LCA_Solver
{
	private:
		int anc[N][P];
		inline void reset(CI now)
		{
			for (RI i=0;i<P-1;++i) if (anc[now][i])
			anc[now][i+1]=anc[anc[now][i]][i]; else break;
		}
	public:
		inline void DFS(CI now=1)
		{
			reset(now); L[now]=++idx; for (RI i=head[now];i;i=e[i].nxt)
			anc[to][0]=now,dep[to]=dep[now]+1,DFS(to); R[now]=idx;
		}
		inline int getLCA(int x,int y)
		{
			if (dep[x]<dep[y]) swap(x,y); RI i;
			for (i=P-1;~i;--i) if (dep[anc[x][i]]>=dep[y]) x=anc[x][i];
			if (x==y) return x;
			for (i=P-1;~i;--i) if (anc[x][i]!=anc[y][i]) x=anc[x][i],y=anc[y][i];
			return anc[x][0];
		}
		inline void clear(void)
		{
			for (RI i=1,j;i<=n;++i) for (j=0;j<P;++j)
			if (anc[i][j]) anc[i][j]=0; else break;
		}
}T;
#undef to
class Segment_Tree
{
	private:
		struct segment
		{
			int ch[2],v;
		}node[N*P<<2]; int rt[N],tot;
		#define lc(x) node[x].ch[0]
		#define rc(x) node[x].ch[1]
		#define V(x) node[x].v
		#define TN CI l=1,CI r=n
		inline void _update(int& now,int lst,CI pos,CI mv,TN)
		{
			now=++tot; node[now]=node[lst]; V(now)+=mv; if (l==r) return;
			int mid=l+r>>1; if (pos<=mid) _update(lc(now),lc(lst),pos,mv,l,mid);
			else _update(rc(now),rc(lst),pos,mv,mid+1,r);
		}
		inline int _query(CI now,CI beg,CI end,TN)
		{
			if (!now) return 0; if (beg<=l&&r<=end) return V(now); int mid=l+r>>1,ret=0;
			if (beg<=mid) ret+=_query(lc(now),beg,end,l,mid);
			if (end>mid) ret+=_query(rc(now),beg,end,mid+1,r); return ret;
		}
	public:
		inline void update(CI x,CI pos,CI mv) { _update(rt[x],rt[x]?rt[x]:rt[x-1],pos,mv); }
		inline int query(CI x,CI beg,CI end) { return _query(rt[x],beg,end); }
		inline void clear(void)
		{
			tot=0; for (RI i=0;i<=mxd;++i) rt[i]=0;
		}
		#undef lc
		#undef rc
		#undef V
		#undef TN
}SEG;
int main()
{
	for (scanf("%d",&t);t;--t)
	{
		RI i; for (scanf("%d%d",&n,&m),i=1;i<=n;++i) scanf("%d",&c[i]);
		for (i=2;i<=n;++i) scanf("%d",&x),addedge(x,i);
		for (dep[1]=1,T.DFS(),i=1;i<=n;++i) d[dep[i]].push_back(i),mxd=max(mxd,dep[i]);
		for (i=1;i<=mxd;++i) for (VI it=d[i].begin();it!=d[i].end();++it)
		{
			SEG.update(i,L[*it],1); SI pre=s[c[*it]].lower_bound(element(L[*it])),nxt=pre; int ct=0;
			if (pre!=s[c[*it]].begin()) --pre,SEG.update(i,L[T.getLCA(*it,pre->y)],-1),++ct;
			if (nxt!=s[c[*it]].end()) SEG.update(i,L[T.getLCA(*it,nxt->y)],-1),++ct;
			if (ct==2) SEG.update(i,L[T.getLCA(pre->y,nxt->y)],1); s[c[*it]].insert(element(L[*it],*it));
		}
		for (i=1;i<=m;++i) scanf("%d%d",&x,&y),x^=ans,y^=ans,printf("%d
",ans=SEG.query(min(dep[x]+y,mxd),L[x],R[x]));
		for (SEG.clear(),T.clear(),i=1;i<=mxd;++i) d[i].clear();
		for (cnt=idx=mxd=ans=0,i=1;i<=n;++i) s[c[i]].clear(),head[i]=0;
	}
	return 0;
}