在数学中的最优化问题中,拉格朗日乘数法(以数学家约瑟夫·拉格朗日命名)是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数,即拉格朗日乘数,又称拉格朗日乘子,或拉氏乘子,它们是在转换后的方程,即约束方程中作为梯度(gradient)的线性组合中各个向量的系数。
比如,要求 f(x,y)在g(x, y) = c 时的最大值,c为常数。先来看图
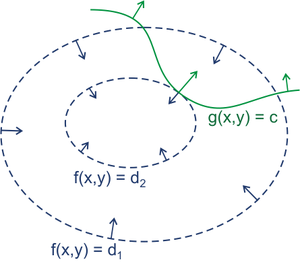
绿线标出的是约束g(x,y) = c的点的轨迹,也是g(x,y)的一条等高线。蓝线是f的等高线,f(x,y)分别取d1 , d2 ,.....dn。箭头表示梯度,和等高线的法线平行。
假设g(x,y) = c 等高线 与 f(x,y) = dn 等高线相交,交点就是同时满足等式约束条件和目标函数的可行域的值,但肯定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优值,即等高线和目标函数的曲线在该点的法向量必须有相同方向,所以最优值必须满足:f(x,y)的梯度 = λ * g(x,y)的梯度,λ是常数,表示左右两边同向。这个等式就是拉格朗日函数L(x,y,λ)对参数求导的结果。
我们先写出拉格朗日函数,
L(x,y,λ) = f(x,y) + λ * (g(x,y) - c)
求解▽L(x,y,λ) 的梯度为0。L(x,y,λ)梯度为0时,则L(x,y,λ)对参数λ的偏导为0,即g(x,y) - c = 0,也是就满足了我们的约束条件g(x,y) = c。这就是拉格朗日乘子λ的神奇之处。
另外 ▽L(x,y,λ) = 0,必须满足
▽f(x,y) = - λ * ▽g(x,y)
为什么呢?我是这样考虑的,不对的地方,请读者指正。
▽L(x,y,λ) 为0,则L(x,y,λ) 对x的偏导等于0,对y的偏导等于0。也就是它在这两个方向上Δx或者Δy趋近于0时,增量ΔL也趋近于0。而L(x,y,λ)是一个复合函数,由 f(x,y)和 λ * (g(x,y) - c)加和得来的,如果某一点(x0,y0)的梯度满足▽f(x,y) = - ▽(λ * (g(x,y) - c))的话,它们梯度的方向正好相反,而且大小相同的话,则可以在x和y方向完全抵消,即L在(x0,y0)处的梯度为0。必然能够得到L(x,y,λ) 对x的偏导等于0,对y的偏导等于0。