直观理解贝叶斯公式
好多同学反应不理解贝叶斯公式,专门写一篇让大家直观的理解贝叶斯公式。
先来一个问题:一机器在良好状态生产合格产品几率是90%,在故障状态生产合格产品几率是30%,机器良好的概率是75%,若一日第一件产品是合格品,那么此日机器良好的概率是多少?
这里需要用到贝叶斯公式,贝叶斯公式一点也不神秘,首先我们要是觉得两个东西之间有关联,那么他们就有联合概率 ,联合概率可以用链式法则表示
,这个是大家都学过的条件概率,A和B同时发生的概率是B发生的概率乘以B发生下A的条件概率,反过来一样成立,所以有:
两边同时除以 ,得:
这就是贝叶斯公式。所以贝叶斯公式的范围非常广泛,只要两个东西有关联,能写出联合概率,那么就可以用贝叶斯公式。
机器有良好和故障两种状态,用A表示。产品有合格和不合格两种状态,用B表示。
直接套用公式算一波:
的概率等于:
所以:
看公式是不是很迷惑?知乎上一个回答给出了很好的图:
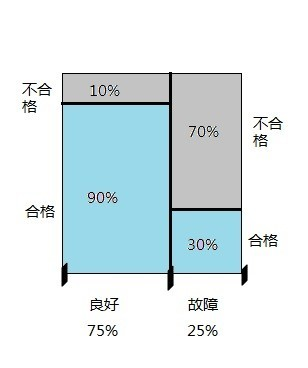
问题要求的机器良好的概率=左下角那个蓝色方格的面积/所有蓝色部分的面积,是不是很好懂?
题目是
一机器在良好状态生产合格产品几率是90%,在故障状态生产合格产品几率是30%,机器良好的概率是75%,若一日第一件产品是合格品,那么此日机器良好的概率是多少?
先验概率是一般情况下机器良好的概率0.75(蓝色面积/总面积),在得知当天有合格产品产出后,灰色面积就没可能了,经过贝叶斯定律的计算后,就得到后验概率0.9(左下角蓝色面积/蓝色总面积)。
https://qb.zuoyebang.com/xfe-question/question/9185bafe39a121b897b612c463830d16.html
一批产品中96%是合格品,检查产品是,一件合格品被误认为是次品的概率是0.02,一件次品被误认为是合格品的概率是0.05,
求在被检查后认为是合格品的产品确是合格品的概率.
设A=任取一产品,经检查是合格品
B=任取一产品,确是合格品
A=B发生A+B不发生A
PA=0.96*0.9

