Motivation
我们希望我们的模型不仅仅是在大多数情况下可用的,还希望它能够应对来自外界的“攻击”,特别是在垃圾邮件分类、恶意软件检测、网络入侵检测等任务中。
这个领域为对抗攻击与防御(Adversarial Attack and Defense),目前攻击是比较容易的而防御比较困难。
What is Attack
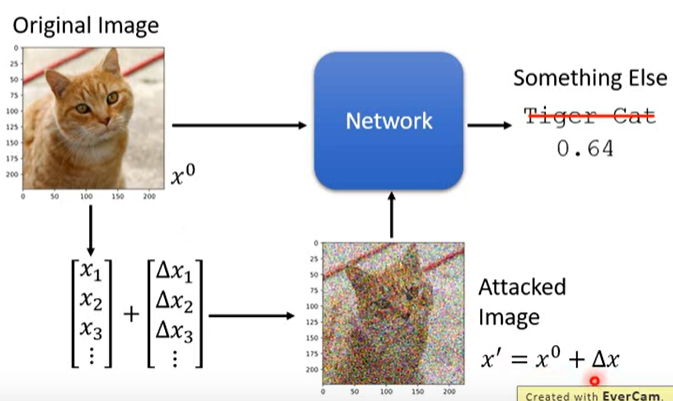
attack就是往原输入(x^0)中添加一些特别的噪声(Delta x)(并不是随机生成的)得到一个稍微有些不同的输入(x'=x^0+Delta x),而模型却得到一个与原输出截然不同的输出。如下图所示,在图像分类任务中,对一张“Tiger Cat”图片添加一些特别的噪声(Delta x)后,人类还能看出它是“Tiger Cat”,但模型却认为它是其它的类别。
Loss Function For Attack
攻击可以分为两种:Non-targeted Attack和Targeted Attack。
How To Train
我们是这样训练一个普通的神经网络的:将输入(x^0)输入到模型后,我们希望模型的输出(y^0)和标签(y^{true})越接近越好,则损失函数为(L_{train}( heta)=C(y^0,y^{true}))。此时输入(x^0)是固定的,我们需要不断调整模型参数( heta),使得(L_{train}( heta))最小。
Non-targeted Attack
如果是Non-targeted Attack,将输入(x'=x+Delta x)输入到模型后,我们希望模型的输出(y')和标签(y^{true})的差异越大越好,则损失函数为(L_{Non-targeted Attack}(x')=-C(y',y^{true})),比(L_{train}( heta))多了一个负号。此时模型参数( heta)是固定的,我们需要不断调整输入(x'),使(L_{Non-targeted Attack}(x'))最小。
Targeted Attack
如果是Targeted Attack,将输入(x'=x+Delta x)输入到模型后,我们希望模型的输出(y')和标签(y^{true})的差异越大越好并且模型的输出(y')与某个(y^{false})越接近越好,其中(y^{false})需要人为选择,则损失函数为(L_{Targeted Attack}(x')=-C(y',y^{true})+C(y',y^{false}))。此时模型参数( heta)是固定的,我们需要不断调整输入(x'),使(L_{Targeted Attack}(x'))最小。
Constraint For Attack
在Attack中,除了要使(L_{Non-targeted Attack}(x'))和(L_{Targeted Attack}(x'))最小之外,我们还希望(x^0)和(x')之间的差异较小,即(d(x^0,x')leqepsilon),其中(epsilon)需要人为选择,这样才能实现真正的Attack。
主要有两种计算(d(x^0,x'))的方法,但在不同的任务中应该有不同的计算方法,因为其代表着人类视角下(x^0)和(x')之间的差异。
L2-norm
L2-norm为(x^0)和(x')中每个像素之差的平方和,即(d(x^0,x')=||x^0-x'||_2=||Delta x||_2=(Delta x_1)^2+(Delta x_2)^2+(Delta x_3)^2+dots)
L-infinity
L-infinity为(x^0)和(x')中每个像素之差的最大值,即(d(x^0,x')=||x^0-x'||_{infin}=||Delta x||_{infty}=max{Delta x_1,Delta x_2,Delta_3,dots})
对于图像中的pixel来讲,也许L-infinity是更有效的计算方法。
How to Attack
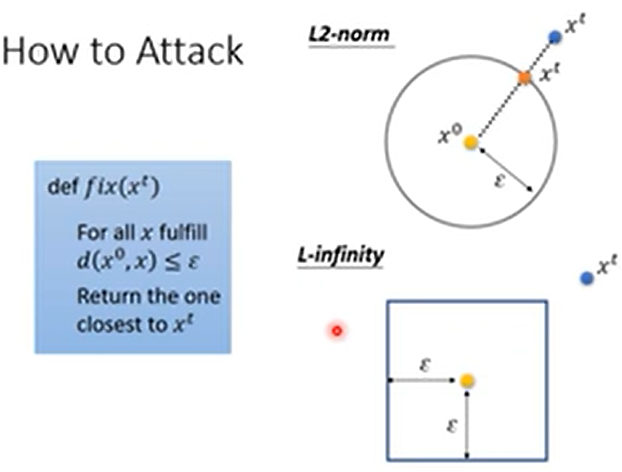
我们在Attack时要训练的参数是输入(x')而非模型参数( heta),在(d(x^0,x')leqepsilon)的情况下使得(L(x'))最小,即(x^*=argmathop{min}_limits {d(x^0,x')leqepsilon}L(x'))。
关于如何训练输入(x')而非模型参数( heta),可以参考下Explainable AI的代码部分,其实就是设置输入(x')的梯度是可追踪的并在定义优化器时传入输入(x')而非模型参数( heta)。

如上图所示,在训练时有两个关键点。第一点是输入(x')应该用(x^0)初始化;第二点是在每个iteration中需要判断保证(d(x^0,x')leqepsilon),具体来讲就是当发现(d(x^0,x')>epsilon)时就需要将(x')修正为所有满足(d(x^0,x)>epsilon)的(x)中与(x')最接近的那个。那要怎么找到所有满足(d(x^0,x)>epsilon)的(x)中与(x')最接近的那个呢?下图中圆形和正方形中的(x)均满足(d(x^0,x)>epsilon),所以中心(x^0)与(x’)连线与圆形或正方形的交点就是要修正的结果。
Attack Approaches
- FGSM (https://arxiv.org/abs/1412.6572)
- Basic iterative method (https://arxiv.org/abs/1607.02533)
- L-BFGS (https://arxiv.org/abs/1312.6199)
- Deepfool (https://arxiv.org/abs/1511.04599)
- JSMA (https://arxiv.org/abs/1511.07528)
- C&W (https://arxiv.org/abs/1608.04644)
- Elastic net attack (https://arxiv.org/abs/1709.04114)
- Spatially Transformed (https://arxiv.org/abs/1801.02612)
- One Pixel Attack (https://arxiv.org/abs/1710.08864)
- ……
虽然有很多方法都可以进行attack,但它们的主要区别在于使用了不同的constraint或者使用了不同的optimization method。
FGSM
FGSM即Fast Gradient Sign Method,本次homework(hw6_AdversarialAttack)就使用了FGSM。
FGSM中输入的更新规则为(x^*=x^0-epsilonDelta x)。它首先计算出损失(L)关于(x)的每个维度的梯度,如果梯度大于0则修改为+1、小于0则修改为-1,也就是说(x^0)的所有维要么(+epsilon)是要么是(-epsilon)。
假设FGSM使用L-infinity计算(d(x^0,x^*)),如果梯度指向左下角那么(x^*)就在方框的右上角;如果gradient指向左上角那么(x^*)就在方框的右下角;因此在FGSM中我们只在意梯度方向而不在意其大小。我们可以认为FGSM使用一个非常大的学习率使(x)飞出正方形,但因为要保证(d(x^0,x')leqepsilon)所以(x^*)就会被限制到方形区域内部。所以就像是“一拳超人”,只攻击一次就达到好的效果。

Black Box Attack
Attack可以分为White Box和Black Box。White Box Attack指模型参数( heta)是已知的,Black Box Attack指模型参数( heta)是未知的。
在Black Box Attack中,我们不知道Black Network的参数( heta)。现假设我们知道Black Network的训练集,那我们就可以使用这份训练集自行训练出一个Proxy Network,然后基于Proxy Network和训练集就可以得到(x'),这个(x')一般也可以成功攻击Black Network。如果Black Network是一个在线API,我们既不知道Black Network的参数也不知道它的训练集,那上传大量输入后就可以得到大量对应的输出,并以这些输入输出对为训练集得到Proxy Network和(x')。
有相关实验证明,Black Box Attack是非常有可能攻击成功的,详见:Delving into Transferable Adversarial Examples and Black-box Attacks(https://arxiv.org/abs/1611.02770)
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!