---恢复内容开始---
出发点
应用统计方法解决模式识别问题时,一再碰到的问题之一就是维数问题。 在低维空间里解析上或计算上行得通的方法,在高维空间里往往行不通。 因此,降低维数有时就会成为处理实际问题的关键。
问题描述
考虑把d维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维。
然而,即使样本在d维空间里形成若干紧凑的互相分得开的集群,当把它们投影到一条直线上时,也可能会是几类样本混在一起而变得无法识别。
但是,在一般情况下,总可以找到某个方向,使在这个方向的直线上,样本的投影能分得开。
问题:如何根据实际情况找到一条最好的、最易于分类的投影线,这就是Fisher判别方法所要解决的基本问题。
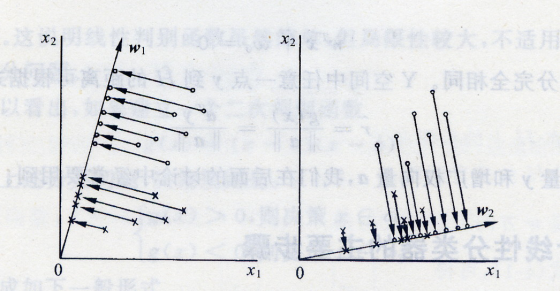
从d维空间到一维空间的一般数学变换方法

Fisher准则函数的定义
(1)几个必要的基本参量



我们希望投影后,在一维Y空间中各类样本尽可能分得开些,即希望两类均值之差越大越好,同时希望各类样本内部尽量密集,即希望类内离散度越小越好。
(2)Fisher准则函数


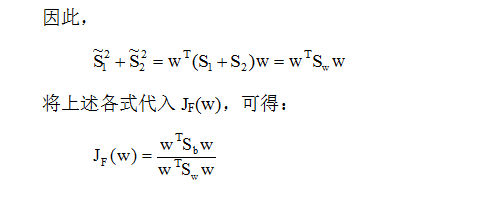

(3)最佳变换向量W*的求取
先修知识:Lagrange乘数法


最佳变换向量的求取




基于最佳变换向量w*的投影
w*是使Fisher准则函数JF(w)取极大值时的解,也就是d维X空间到一维Y空间的最佳投影方向。有了w*,就可以把d维样本x投影到一维,这实际上是多维空间到一维空间的一种映射,这个一维空间的方向w*相对于Fisher准则函数JF(w)是最好的。 利用Fisher准则,就可以将d维分类问题转化为一维分类问题,然后,只要确定一个阈值T,将投影点yn与T相比较,即可进行分类判别。
