一。情有独钟
对数据结构情有独钟,打算慢慢把jdk里的实现都读一遍,发现其中的亮点,持续更新。
二。ArrayList
这应该是我们学习java最早接触的到的数据结构,众所周知,数组在申请了内存之后,无法扩展;而数组队列,是实现了动态扩容的功能,意义上是为动态数组,实际上的数组扩容是不允许在原地址上伸长的,很简单,因为在你申请的数组空间之后,可能存在别的被申请掉的内存;要实现动态数组,必然是新申请一个更大的连续内存空间,并替换到原来的引用中。
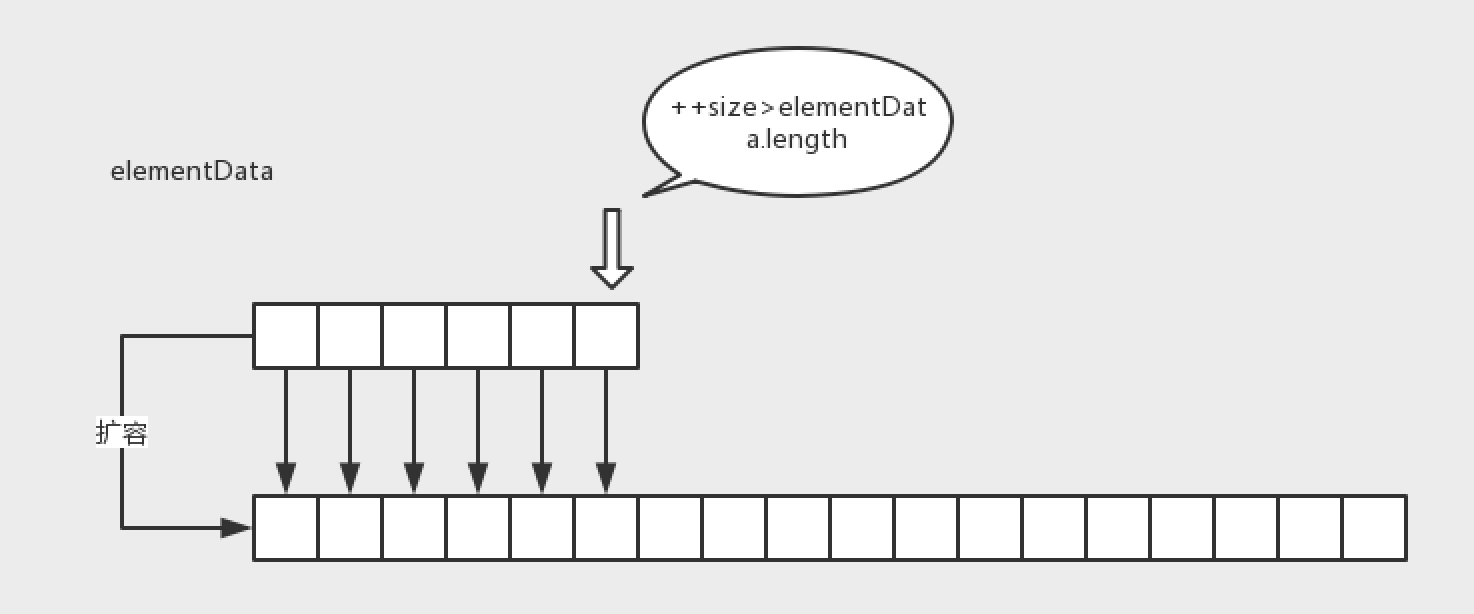
从构造函数,可以清楚看到,elementData,就是这个存储数据的内存地址。

然后,找到添加的接口,add;在真正赋值之前,会进行grow方法。


可以看到,真正干活的是这个copyof,找到最后,就是这个方法。
首先这个泛型数组,会先判断一下如果是Object父类,则直接new Object,如果不是则调用Arrays的接口创建,才去新建一个数组,然后就会去拷贝数组到新的数组,并返回这个被拷贝的数组。
public static <T,U> T[] copyOf(U[] original, int newLength, Class<? extends T[]> newType) { @SuppressWarnings("unchecked") T[] copy = ((Object)newType == (Object)Object[].class) ? (T[]) new Object[newLength] : (T[]) Array.newInstance(newType.getComponentType(), newLength); System.arraycopy(original, 0, copy, 0, Math.min(original.length, newLength)); return copy; }
它的get方法,简单判断一下是否大于元素容量,防止内存泄漏的操作。
public E get(int index) { rangeCheck(index); return elementData(index); }
它的remove方法,是将这个位置之后的所有元素,前移一个位置,并将最后的元素设置为null。
public E remove(int index) { rangeCheck(index); modCount++; E oldValue = elementData(index); int numMoved = size - index - 1; if (numMoved > 0) System.arraycopy(elementData, index+1, elementData, index, numMoved); elementData[--size] = null; // clear to let GC do its work return oldValue; }
它提供的排序接口,设计的是传入一个比较器,可以自定升序还是降序,最终一个分支使用的是mergeSort。最后还校验了一下modcount,前后是否相等,如果不相等抛出并发异常,有点CAS的思想。
@Override @SuppressWarnings("unchecked") public void sort(Comparator<? super E> c) { final int expectedModCount = modCount; Arrays.sort((E[]) elementData, 0, size, c); if (modCount != expectedModCount) { throw new ConcurrentModificationException(); } modCount++; }
public static void sort(Object[] a) { if (LegacyMergeSort.userRequested) legacyMergeSort(a); else ComparableTimSort.sort(a, 0, a.length, null, 0, 0); }
长度小于7插入排序,反正是个n平方的排序,
private static void mergeSort(Object[] src, Object[] dest, int low, int high, int off) { int length = high - low; // Insertion sort on smallest arrays if (length < INSERTIONSORT_THRESHOLD) { for (int i=low; i<high; i++) for (int j=i; j>low && ((Comparable) dest[j-1]).compareTo(dest[j])>0; j--) swap(dest, j, j-1); return; } // Recursively sort halves of dest into src int destLow = low; int destHigh = high; low += off; high += off; int mid = (low + high) >>> 1; mergeSort(dest, src, low, mid, -off); mergeSort(dest, src, mid, high, -off); // If list is already sorted, just copy from src to dest. This is an // optimization that results in faster sorts for nearly ordered lists. if (((Comparable)src[mid-1]).compareTo(src[mid]) <= 0) { System.arraycopy(src, low, dest, destLow, length); return; } // Merge sorted halves (now in src) into dest for(int i = destLow, p = low, q = mid; i < destHigh; i++) { if (q >= high || p < mid && ((Comparable)src[p]).compareTo(src[q])<=0) dest[i] = src[p++]; else dest[i] = src[q++]; } }
三。PriorityQueue
优先队列,读作优先写作二叉树,也叫堆(大顶堆,小顶堆)。
它的实现方法是数组,使用数组做二叉树,每个元素e[i]的孩子为e[2*i+1],e[2*i+2]。
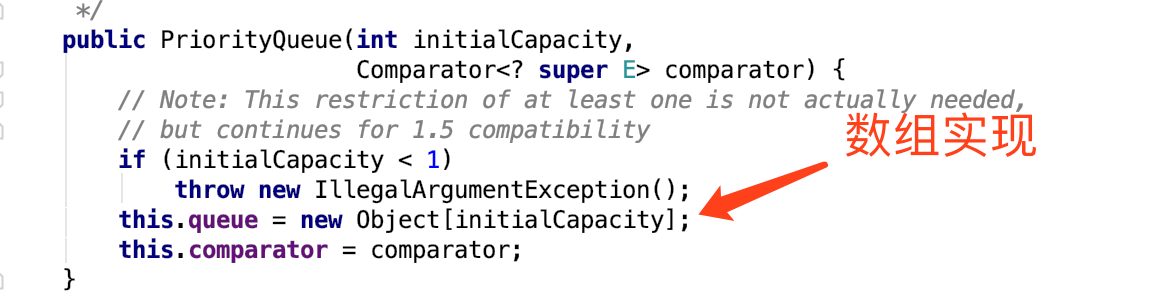
找到添加元素的方法;比较器为空的时候;它从末尾插入,先找出父亲,如果父节点比自己大,则继续往上,将父节点往下移动,直到找到比它小的位置插入,默认是一个小顶堆。

public boolean offer(E e) { if (e == null) throw new NullPointerException(); modCount++; int i = size; if (i >= queue.length) grow(i + 1); size = i + 1; if (i == 0) queue[0] = e; else siftUp(i, e); return true; } private void siftUpComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>) x; while (k > 0) { int parent = (k - 1) >>> 1; Object e = queue[parent]; if (key.compareTo((E) e) >= 0) break; queue[k] = e; k = parent; } queue[k] = key; }
弹出操作就是把堆定元素拿走,然后从末尾拿出一个元素,放在堆顶,不断地下沉。
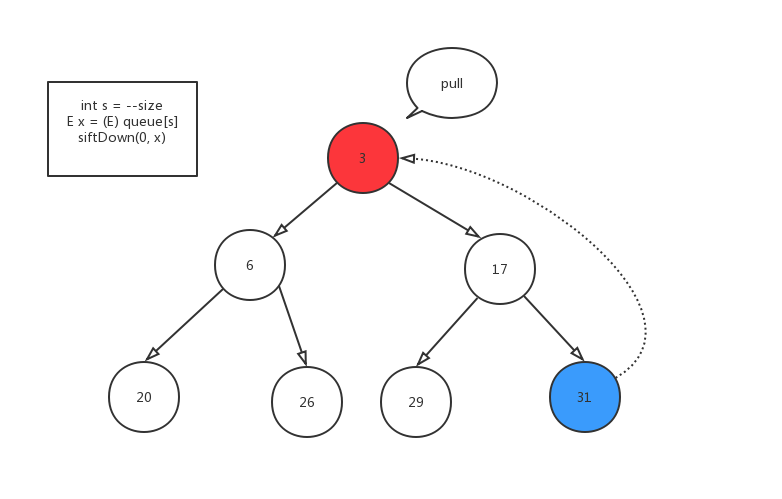
public E poll() { if (size == 0) return null; int s = --size; modCount++; E result = (E) queue[0]; E x = (E) queue[s]; queue[s] = null; if (s != 0) siftDown(0, x); return result; } private void siftDownComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>)x; int half = size >>> 1; // loop while a non-leaf while (k < half) { int child = (k << 1) + 1; // assume left child is least Object c = queue[child]; int right = child + 1; if (right < size && ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0) c = queue[child = right]; if (key.compareTo((E) c) <= 0) break; queue[k] = c; k = child; } queue[k] = key; }
四。ArrayBlockingQueue
看腻了数组队列,我们来看多线程的阻塞队列是怎么实现的;
粗浅的看,它是在多线程中保持一致性的一种数据结构,保持一致性只有两种思路:(1)假设它发生了冲突,则必然加锁(悲观)(2)假设他不一定产生冲突,CAS无锁实现(乐观);
当然,它最基本的数据都是数组;
public boolean offer(E e) { checkNotNull(e); final ReentrantLock lock = this.lock; lock.lock(); try { if (count == items.length) return false; else { enqueue(e); return true; } } finally { lock.unlock(); } }
从以上的代码,非常直白,首先只能有一个线程进入这个数据操作的代码,并且队列是不扩容的,一旦达到最大容量,则直接拒绝,返回false;
private void enqueue(E x) { // assert lock.getHoldCount() == 1; // assert items[putIndex] == null; final Object[] items = this.items; items[putIndex] = x; if (++putIndex == items.length) putIndex = 0; count++; notEmpty.signal(); }
正如我们认知的一样,它是一个先进先出的队列,所以在下标达到最大长度之后,会reset成0,并且入队之后,还会唤醒一个事件,就是非空;
我们还有一个put方法可以入队;
public void put(E e) throws InterruptedException { checkNotNull(e); final ReentrantLock lock = this.lock; lock.lockInterruptibly(); try { while (count == items.length) notFull.await(); enqueue(e); } finally { lock.unlock(); } }
这个队列相当于不是快速失败,而是将当前线程park,使用一个condition的await,让线程等待;
它的获取方法take,我们来阅读以下;
public E take() throws InterruptedException { final ReentrantLock lock = this.lock; lock.lockInterruptibly(); try { while (count == 0) notEmpty.await(); return dequeue(); } finally { lock.unlock(); } }
使用的是一个线程中断锁,并且在队列为空的时候,park当前线程;与入队方法enqueue成对应,有元素进来的时候会signal阻塞在此的线程;
private E dequeue() { // assert lock.getHoldCount() == 1; // assert items[takeIndex] != null; final Object[] items = this.items; @SuppressWarnings("unchecked") E x = (E) items[takeIndex]; items[takeIndex] = null; if (++takeIndex == items.length) takeIndex = 0; count--; if (itrs != null) itrs.elementDequeued(); notFull.signal(); return x; }
这个操作,在结束的时候会唤醒阻塞在put的线程,告诉他有位置可以进来了。
而此外,它还提供了带等待时间的阻塞方法。
public boolean offer(E e, long timeout, TimeUnit unit) public E poll(long timeout, TimeUnit unit)
然后它的size,也是需要获取重入锁的,不是非阻塞的。

这么看,它有点像--消息队列。
五。ConcurrentLinkedQueue
并发无锁链表队列,因为线程不会被park,所以效率较高,但是可能引起cpu运算过高。它是在普通链表的基础上,添加了并发的控制, 并采用CAS原子操作保证内存的有序写入。
它的基本元素,Node,只有两个属性,原子的item和next。
java.util.concurrent.ConcurrentLinkedQueue.Node Node<E> volatile E item; volatile Node<E> next;
初始化的时候,head和tail都指向new出来的一个Node上。
head = tail = new Node<E>(null);
我们只需要关心它的添加(offer)和获取(poll)接口是什么样的流程就可以了。
offer接口
public boolean offer(E e) { checkNotNull(e); final Node<E> newNode = new Node<E>(e); // 快照 for (Node<E> t = tail, p = t;;) { Node<E> q = p.next; if (q == null) {// 如果是队尾 则尝试CAS插入 if (p.casNext(null, newNode)) { // 如果tail节点在插入前不是指向末尾节点,则更新tail // 延迟更新也没事,始终会有一个线程更新成功 if (p != t) casTail(t, newNode); // Failure is OK. return true; } // Lost CAS race to another thread; re-read next } else if (p == q) // 由于poll方法,会将节点自引用以便gc,所以要从头节点开始找 p = (t != (t = tail)) ? t : head; else // 如果t的引用地址和tail的一致,则p往下找(p=p.next的意思) // 如果不一致,则直接拿到tail并赋值给p p = (p != t && t != (t = tail)) ? t : q; } }

在单线程插入的时候,插入完成之后如上图。如果继续插入,则p和t不相等,会更新tail的值,这就是快照时候tail不是指向最后一个节点才会执行的逻辑。
如果是多线程插入,在上一个线程没有更新tail的时候,它可能会一直p=p.next的流程,这时候另一个线程更新了tail的地址,这时候需要刷新t的位置。
offer和offer方法的多线程冲突,主要在于tail指针的位置问题。
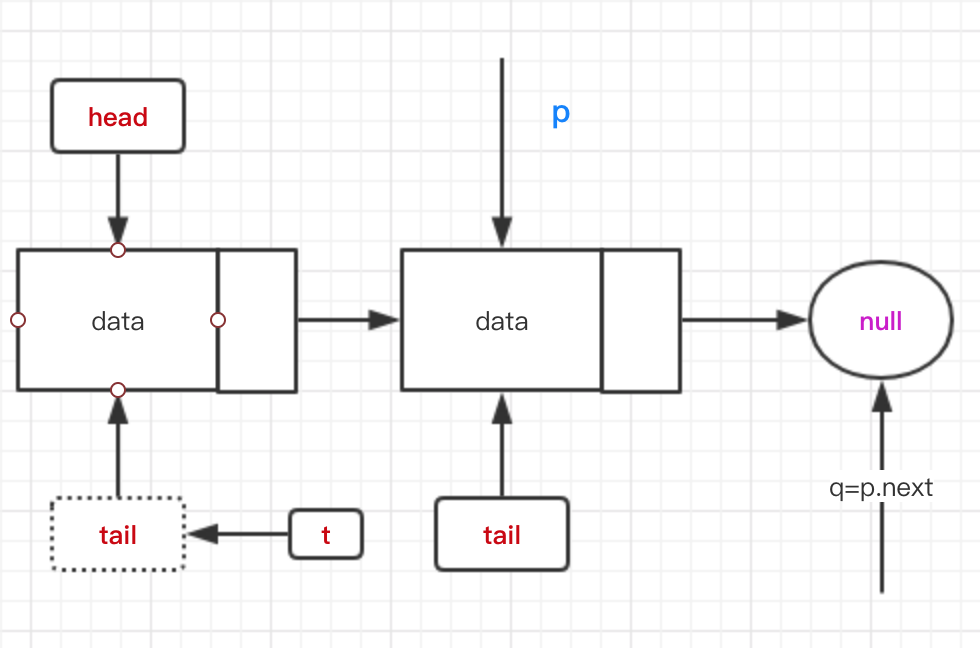
接下来我们看看poll方法。
public E poll() { restartFromHead: for (;;) { for (Node<E> h = head, p = h, q;;) { E item = p.item; // 出队是更新节点data为null if (item != null && p.casItem(item, null)) { // 如果p节点的下一个不为空则head指向下一个,否则指向p updateHead(h, ((q = p.next) != null) ? q : p); return item; } else if ((q = p.next) == null) {// 如果下一个是null 则更新头节点为自引用 updateHead(h, p); return null; } else if (p == q)// 撞到了自引用 则跳出循环重新copy快照 continue restartFromHead; else p = q;// p = p.next的意思 } } }
我们假设队列的情况是。h还是指向head原地址,p经过一步之后会指向h的next。这时候要将p的Node的item更新为null,并设置head指针,而且p.next不为空,则head会更新到p.next上。
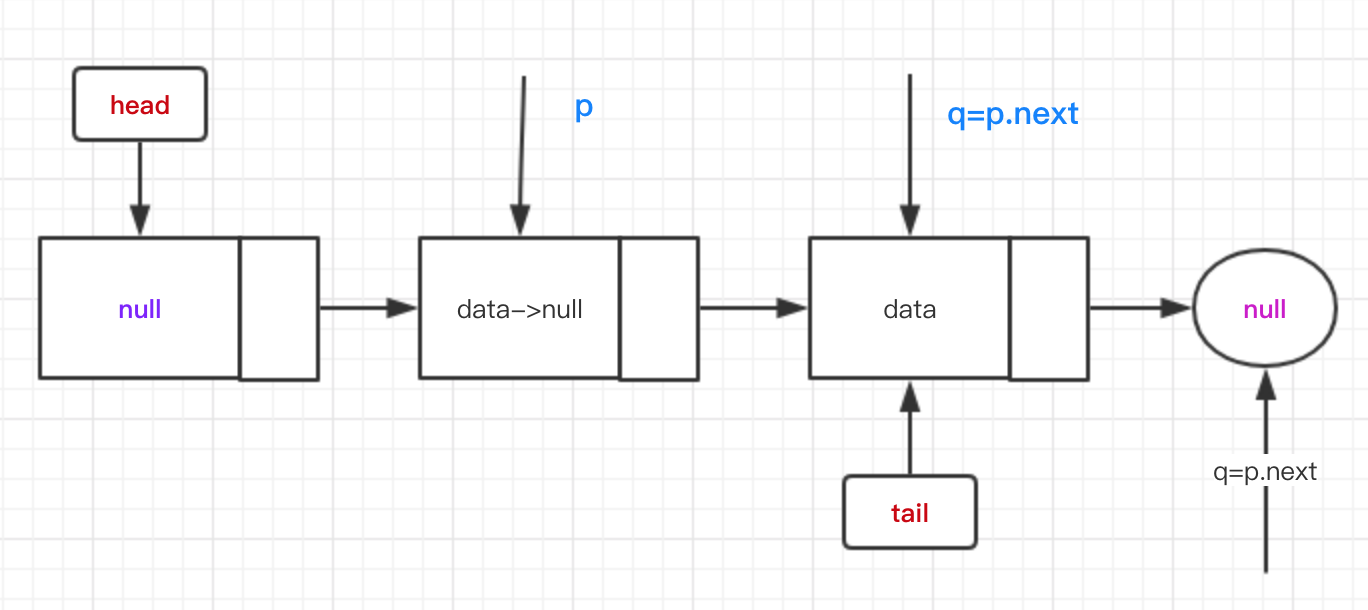
更新之后的状态是。

如果这个时候tail没有更新,还是指向最初的那个节点,也就是offer与poll的冲突。这时候offer就会走第二个else if条件,拿到head。
只有三四行代码,却那么多场景,真是大师作品。写得这么难懂,是因为可以节省CAS指令,我们自己写的CAS操作是util success,这样可能会执行很多条,它这里的head和tail更新不强制一定成功。