题目描述
给定一个字符串,请你找出其中不含有重复字符的最长子串的长度。
示例 1
输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2
输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3
输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
示例 4
输入: s = "" 输出: 0
解答
我们先从最简单的方法开始,最容易想到的算法就是暴力枚举。我们可以遍历出这个字符串当中所有的子串,之后再判断这个子串当中有没有出现重复的元素。如果没有重复的元素,那么我们就更新答案。但是这种方法的复杂度很高,下面我们进行第一个优化。
思考一个问题,在不能有重复字符的限制下,我们真的有必要枚举所有的子串吗?
其实是没有的,在这个规则的限制下,对于字符串当中的每一个起始位置,我们能找到的最长的合法子串必然是确定而且是唯一的。换句话说,对于一个确切的开头而言,我们只需要顺着它一直往后遍历,如果遇到的字符串没有出现过就继续,如果已经出现过了,那么当下的字符串就是这个开头对应的最佳答案。
我们用样例举个例子:
假设 s = abcabcbb
我们从 s[0] 开始,我们遍历 b,再遍历 c,接着遍历 a,a 已经出现过了,所以 abc 就是以 s[0] 开头的最佳答案。对于 s 当中的每一个位置,我们都可以找到它对应的局部最佳答案。之后,我们只需要在这当中找出最大的长度即可。
我们用 Python 写出代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
ret = 0
n = len(s)
if n == 1:
ret = 1
else:
for i in range(n):
char_set = set()
char_set.add(s[i])
mid_ret = 1
for j in range(i+1, n):
if s[j] in char_set:
break
else:
char_set.add(s[j])
mid_ret = mid_ret + 1
ret = max(mid_ret, ret)
return ret
这种方法的复杂度就很好算了,对于 s 而言,它一共有 n 个位置可以作为起始,每个起始位置,最多遍历 n 次,所以整体的复杂度应该是 0(n^2)。
滑动窗口解法
假设原始字符串 s 如下:
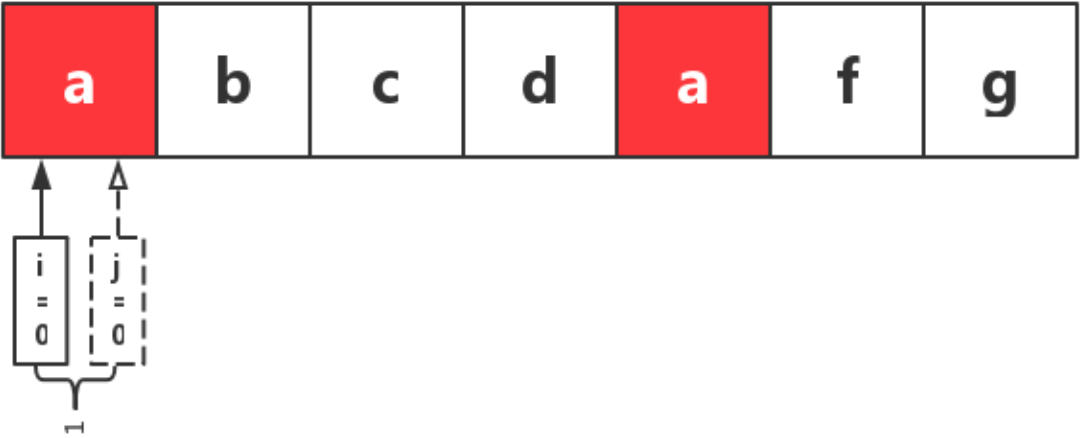
从左侧开始遍历字符串 s,以 i 标记窗口左侧,j 标记窗口右侧,初始时,i=0,j=0,即开头 a 所在的位置,此时,窗口大小为 1。
然后,将 j 右移,逐步扩大窗口,依次经过 b、c、d,此时,窗口内均为重复的字符,继续右移 j。

当 j 移动到 d 后面的 a 所在位置时,对应字符 a 在窗口中已经存在,此时,窗口大小为 5,去除当前重复的一位,窗口大小为 4。此时窗口内的字符串为 abcd。
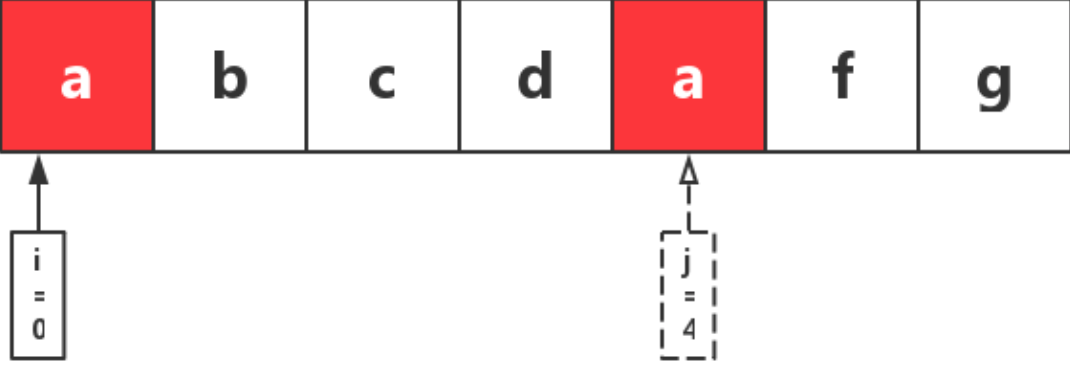
找到窗口中已存在的该字符所在位置,并将 i 移动到该位置的下一位。

此时为第二个窗口。
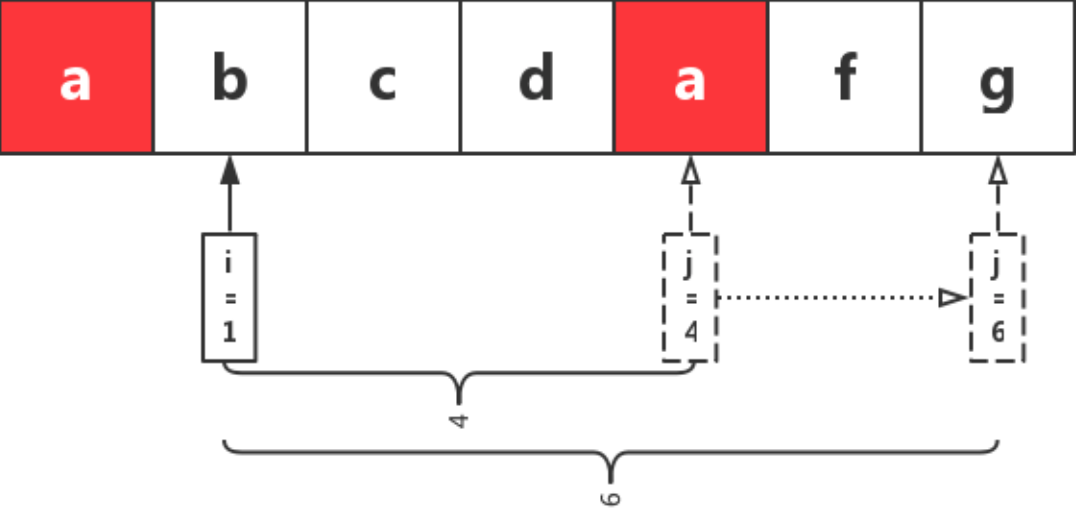
继续重复之前的操作,直到 j 移动到字符串最后一位停止。
代码实现
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if not s:
return 0
rec = list()
n = len(s)
max_len = 0
cur_len = 0
for i in range(n):
if s[i] not in rec:
rec.append(s[i])
cur_len += 1
else:
index = rec.index(s[i])
rec = rec[index+1:]
rec.append(s[i])
cur_len = len(rec)
max_len = max(max_len, cur_len)
return max_len